Домашнее задание : 1)Составьте опорный конспект по теме

Конспект урока математики 

 Дата

89	90	91	92	3	4
8.05.20 11.05.20		8.06.20 9.06.20	1.06.20 2.06.20

Группа № 89 профессия мастер по ремонту и обслуживанию автомобилей курс 1

Группа №90 профессия повар, кондитер курс1

Группа №91 профессия машинист крана(крановщик)

Группа №92 профессия тракторист-машинист сельскохозяйственного производства

Группа №3 специальность механизация сельского хозяйства

Группа № 4 специальность Техническая эксплуатация подъемно-транспотных, строительных дорожных машин и оборудования (по отраслям)

Тема урока: «Производная степенной функции»

Форма работы: индивидуальная, электронное обучение.

Тип урока: урок изучения нового материала.

Цель урока: получить знания о производной степенной функции и её применении к решению задач.

  Изучаемая литература: Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа.

 10-11 классы: учеб.для общеобразоват.организаций: базовый и углубл.уровени./Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.- 5 изд.- М.: Просвещение, 2018г

 Интернет- ресурсы: Математика в открытом колледже http://www.mathematics.ru

                                                    Ход занятия:

1. Организационный этап. Мотивационный модуль

Ребята, сегодня, вы познакомитесь с темой «Производная степенной функции», рассмотрите задания по нахождению производной производной степенной функции.

1. Основная часть. Объясняющий модуль.

План изучения: 1)понятие производной степенной функции

                                    2) вычисление производной степенной функции

                       3) правила вычисления производных одночлена и многочлена

                                 

  Формула для вычисления производной степенной функции xⁿ, где n – произвольное натуральное число, такова:

(xⁿ) ' =nx^n-1

Нам уже известна формула производной функции х²: (x²)’=2x.

Пользуясь формулой дифференцирования произведения, получаем:

(x³) ' = (x²·x) ' = (x²) ' · x + x² · (x) ' = 2x·x+x²·1 = 3x²;

(x⁴) ' = (x³·x) ' = (x³) '·x+x³·(x) ' = 3x²·x+x³·1 = 4x³.

Заметим, что

(x²) ' = 2x^2-1

(x³) ' = 3x^3-1

(x⁴)’=4x^4-1

Т.е. для n, равного 2, 3 и 4, формула (1) доказана. Продолжая аналогичные рассуждения, нетрудно убедиться в справедливости формулы (1) для n, равного 5, 6 и т.д.

Пример 1.

Докажем что, 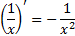, при .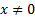

Решение:

1. представим как х^-1;
2. воспользуемся формулой (1): (х^-1)’=-1·x^-1-1=-x^-2;
3. вернемся к первоначальному виду

.

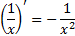 В более сложных случаях пользуются формулой

Формула для вычисления производной степенной функции (kx+b)^p:

((kx+b)^p) ' = pk(kx+b)^p

  Ключевые моменты:

1. Производная суммы двух функций всегда равна сумме производных: (f+g)′=f′+g′

2. По аналогичным причинам производная разности двух функций равна разности двух производных: (f−g)′=f′−g′;

3. Если у функции присутствует множитель константа, то эту константу можно выносить за знак производной: (c⋅f)′=c⋅f′;

4. Если вся функция представляет собой константу, то ее производная всегда ноль: (c)′=0

Давайте посмотрим, как все это работает на реальных примерах. Итак:

y=x5−3x2+7

Записываем:

(x5−3x2+7)′=(x5)′−(3x2)′+7′=5x4−3(x2)′+0=5x4−6x

В этом примере мы видим и производную суммы, и производную разности.

Переходим ко второй функции:

f(x)=3x2−2x+2

Записываем решение:

(3x2−2x+2)′=(3x2)′−(2x)′+2′==3(x2)′−2x′+0=3⋅2x−2⋅1=6x−2

 

Пример

Найдем производную функции (3х-1)⁷.

Решение:

воспользуемся формулой (2)

((3х-1)⁷)’=21(3x-1)⁶.

Тренировочный модуль

Пример 1

Вычислить f’(9), если .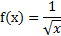

Решение:

;

.

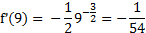Пример 2

Доказать, что 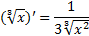на промежутке:

1. x>0;
2. x<0.

Доказательство:

1. если x>0, то 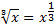и по формуле (1) получаем:

.

1. если x<0, то 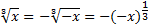и по формуле (2) получаем:

.

Домашнее задание: 1)Составьте опорный конспект по теме

Выполните задание

1) f(x)=5х+7 2) f(x)=-3x²+2

3) f(x)=4x       4) f(x)=-5x-7

Конспект и выполненные задания отправить  в ЛС вВК