Межрегиональный центр переподготовки специалистов
Экзамен
По дисциплине: Математика (1сем.)
Выполнила: Свистуненко И.Г.
Группа: ПБТ-23
Вариант: 03
Проверил: ___________________
Новосибирск, 2012 г
Билет № 19
Методы интегрирования тригонометрических функций.
1) Рассмотрим интеграл от тригонометрических функций 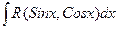 .
.
Этот интеграл с помощью подстановки 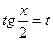 всегда сводиться к интегралу от рациональной функции. Выразим Sin x, Cos x и dx через
всегда сводиться к интегралу от рациональной функции. Выразим Sin x, Cos x и dx через 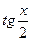 , то есть через t.
, то есть через t.
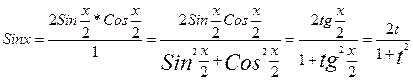 .
.
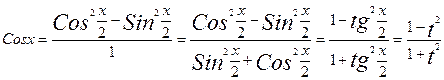 .
.
Если 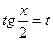 , то
, то  , а
, а 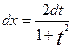 .
.
Пример: 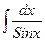 .
. 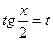 , тогда
, тогда 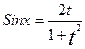 ,
, 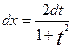 .
.
Следовательно,  .
.
Подстановка 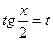 даёт возможность проинтегрировать всякую функцию вида R(Sin x, Cos x).
даёт возможность проинтегрировать всякую функцию вида R(Sin x, Cos x).
Поэтому эту подстановку называют универсальной.
2) Рассмотрим интегралы вида:
а) 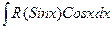 .
.
Используют в этом случае подстановку Sin x = t, а Cos x dx = dt.
б)  .
.
Используют подстановку Cos x = t, -Sin x = dt.
3) Рассмотрим интегралы 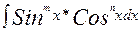 .
.
а) если Sin x и Cos x входят только в чётных степенях, то используют подстановку tg x = t, так как 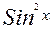 и
и 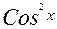 выражаются рационально через tg x.
выражаются рационально через tg x.
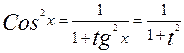 ;
; 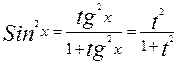 .
.
x=arctgt,  .
.
б) если одно из чисел m и n нечетно, то этот интеграл сводиться к интегралу от рациональных функций подстановками Sin x =Z или Cos x=Z.
4) Для нахождения интегралов 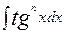 и
и  . Используют подстановку tgx=t,
. Используют подстановку tgx=t,  (ctgx=t)
(ctgx=t)
5) Рассмотрим интегралы вида:
 ;
; 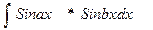 ;
; 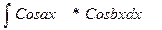 .
.
Эти интегралы находятся путем разложения на слагаемые по формулам:
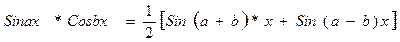
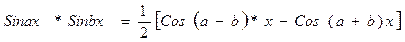

Выпуклость и вогнутость графика функции. Точки перегиба.
Если в некотором интервале кривая расположена ниже любой своей касательной, то она называется выпуклой вверх, а если она расположена выше любой своей касательной, то она называется выпуклой вниз в этом интервале.
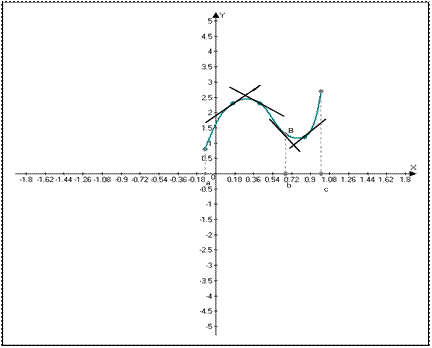
Рис. 1. Точка B – точка перегиба
Точкой перегиба называется точка на кривой, где меняется направление её выпуклости.
Направление выпуклости кривой y=f(x) характеризуется знаком второй производной  :
:
если в некотором интервале 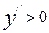 , то кривая выпукла вниз, то есть,
, то кривая выпукла вниз, то есть,
вогнута, а если 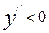 , то кривая выпукла вверх, то есть, выпукла,
, то кривая выпукла вверх, то есть, выпукла,
в этом интервале.
Абсциссы точек перегиба кривой y=f(x) находятся по следующему правилу:
1. Находится  и точки x, в которых
и точки x, в которых 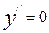 или не существует и которые лежат внутри области определения функции.
или не существует и которые лежат внутри области определения функции.
2. Определить знак  слева и справа от каждой из этих точек. Исследуемая точка x будет абсциссой точки перегиба, если по разные стороны от неё
слева и справа от каждой из этих точек. Исследуемая точка x будет абсциссой точки перегиба, если по разные стороны от неё  имеет разные знаки.
имеет разные знаки.
Пример: Задана кривая 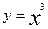 . (рис. 2)
. (рис. 2)
Исследуем её на выпуклость, вогнутость, перегиб.
Находим 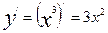 ;
; 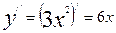 .
.
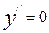 , 6x=0, отсюда x=0.
, 6x=0, отсюда x=0.
При x<0, получаем 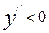 . Следовательно, кривая выпуклая.
. Следовательно, кривая выпуклая.
При x>0, получаем 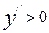 . Значит, кривая вогнута. Следовательно, x=0 – абсцисса точка перегиба.
. Значит, кривая вогнута. Следовательно, x=0 – абсцисса точка перегиба.
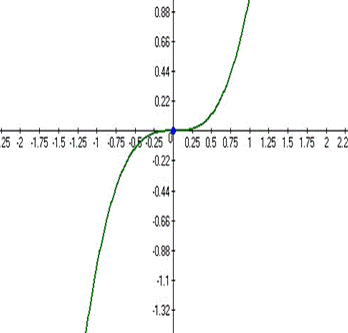
Рис. 2. Кривая 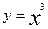
3. Вычислить предел 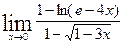 .
.
При подстановке предельного значения аргумента получаем неопределенность вида 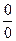 .
.
 Для нахождения предела в этом случае используем правило Лопиталя: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных,
Для нахождения предела в этом случае используем правило Лопиталя: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных,
то есть, 
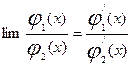 , при
, при  или
или 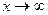 .
.
Следовательно, 
4. Составить уравнение касательной плоскости и нормали к поверхности 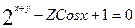 в точке (0; 0; 2).
в точке (0; 0; 2).
Если поверхность задана уравнением F(x; y; z)=0 и точка 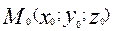 лежит на ней, то касательная плоскости к поверхности в точке
лежит на ней, то касательная плоскости к поверхности в точке 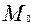 определяется уравнением:
определяется уравнением:
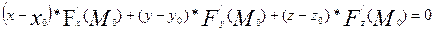 ,
,
а нормаль к поверхности в точке 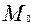 определяется уравнением:
определяется уравнением:
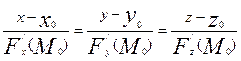 .
.
Находим частные производные 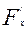 ,
, 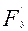 ,
, 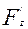 .
.
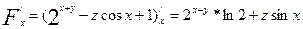

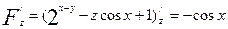
Вычислим значения частных производных в точке (0; 0; 2)
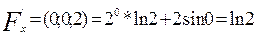
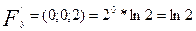
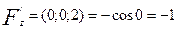
Запишем уравнение искомой касательной плоскости
(x-0)*ln2+(y-0)ln2+(z-2)*(-1)=0.
Ln2*x+ln2*y-z+2=0.
Запишем уравнение нормали
 .
.
5. Найти интеграл 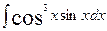
Используем подстановку Cosx=t.
Продифференцируем это равенство: -Sinxdx=dt;
Sinxdx=-dt
Тогда  .
.
6. Вычислить интеграл 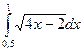
Используем подстановку  , тогда 4x-2=
, тогда 4x-2= 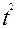 ;
; 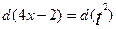 ; 4dx=2tdt;
; 4dx=2tdt;
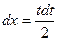
Если x=1, получаем 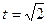 .
.
Если x=0,5, получаем t=0.
Следовательно, 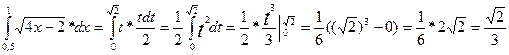 .
.
7. Исследовать сходимость интеграла 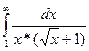 .
.
По определению несобственного интеграла в этом случае получаем
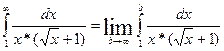 .
.
Найдем 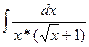 . Используем подстановку
. Используем подстановку 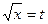 , тогда
, тогда  ;
;
dx=2tdt.
Следовательно, 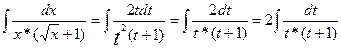
Разложим подынтегральную дробь на сумму двух элементарных дробей.
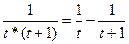 .
.
Следовательно,  .
.
Тогда 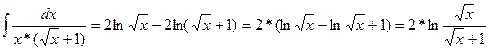 .
.
Таким образом,
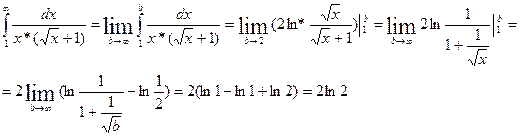
Следовательно, несобственный интеграл сходиться.
8. Найти площадь фигуры, ограниченной линиями  ,
, 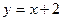 .
.
Сделаем чертеж. (рис. 3)
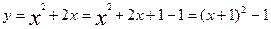 ;
;
Ветви параболы направлены вверх.
Вершина её – точка A(-1;-1).
Найдем точки пересечения параболы с осями координат. Если x=0; y=0. Парабола проходит через начало координат.
Если y=0, то 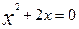 ; x(x+2)=0;
; x(x+2)=0; 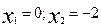 .
.
Парабола пересекает ось OX в точках 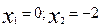 . Для построения прямой
. Для построения прямой 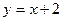 возьмем две точки B(0;2) и C(-2;0).
возьмем две точки B(0;2) и C(-2;0).
Найдем точки пересечения заданных линий.
Для этого решим систему уравнений
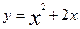 ;
; 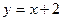

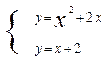 ;
; 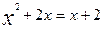 ;
;  ;
; 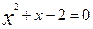 ;
; 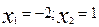
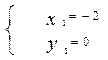 ;
; 


Рис. 3. Парабола 
Если на интервале [a;b] фигура ограничена двумя линиями 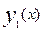 и
и 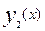 , то площадь такой фигуры находиться по формуле:
, то площадь такой фигуры находиться по формуле:
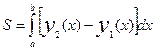 (
(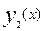 >
>  )
)
В нашей задаче a=-2; b=1; 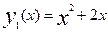 ;
;  . Таким образом,
. Таким образом, 
 2020-08-05
2020-08-05 106
106






