Доведення.
При доведенні слід розглянути 2 випадки.
1. Елементи 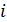 та
та 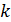 , над якими здійснюється транспозиція, знаходяться поруч:
, над якими здійснюється транспозиція, знаходяться поруч:
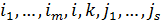
Зауважимо, що після транспозиції положення 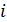 та
та 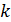 відносно інших елементів не зміниться. Таким чином, якщо
відносно інших елементів не зміниться. Таким чином, якщо 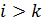 , то вони створюють інверсію і після транспозиції інверсій стане на одну менше. Якщо
, то вони створюють інверсію і після транспозиції інверсій стане на одну менше. Якщо 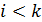 , то загальна кількість інверсій навпаки збільшиться на одну.
, то загальна кількість інверсій навпаки збільшиться на одну.
Отже парність перестановки змінюється.
2. Між елементами 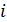 та
та 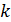 , над якими здійснюється транспозиція, знаходяться інші елементи:
, над якими здійснюється транспозиція, знаходяться інші елементи:
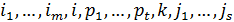
Зробимо транспозицію поступово.
Будемо міняти місцями 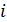 та сусідній справа, поки
та сусідній справа, поки 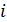 не поміняється із
не поміняється із 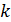 . Для цього буде необхідно зробити t+1 транспозицій.
. Для цього буде необхідно зробити t+1 транспозицій.
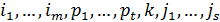
Щоб поставити 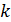 на місце
на місце 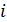 , необхідно зробити
, необхідно зробити 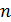 транспозицій із сусідами зліва. Загалом буде зроблено 2t+1 транспозицій, тобто в наслідок попереднього випадку парність перестановки змінюється.
транспозицій із сусідами зліва. Загалом буде зроблено 2t+1 транспозицій, тобто в наслідок попереднього випадку парність перестановки змінюється.
Теорему доведено.
___________________________________
Означення. Лінійний простір називається n-вимірним, якщо в ньому існує n лінійно незалежних векторів, а будь-яка система з n+1 вектора лінійно залежна.
З'ясуємо вимірність арифметичного простору.
Доведемо таку теорему.
Теорема. При 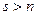 система векторів
система векторів
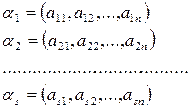
арифметичного простору лінійно залежна.
Доведення.
Розглянемо рівність (*) з означення лінійно залежної і лінійно незалежної системи:
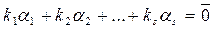
З'ясуємо, при яких 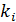 вона виконується:
вона виконується:

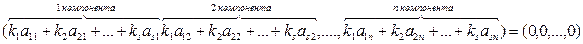
З цієї векторної рівності отримаємо п-числових різностей.
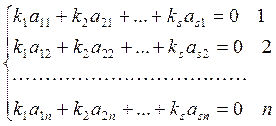
Отримали систему n-рівнянь з s-невідомими. Ця система завжди сумісна тому що вона має принаймні один нульовий розв'язок.
Але за допомогою елементарних перетворень вона зводиться до кінцевого вигляду, де кількість рівнянь менша за кількість невідомих.
Повертаючись до рівності (*) приходимо до висновку що рівність (*) виконується коли принаймі одне з 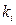 -тих не дорівнює нулю, тому
-тих не дорівнює нулю, тому 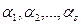 -лінійно залежні.
-лінійно залежні.
Наслідок. Будь-яка система з n + 1 вектора з п-компонентами є лінійно-залежна. Це негайно випливає, якщо з покласти 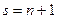 .
.
З цього випливає, що вимірність арифметичного простору не більш ніж: п. Для того, щоб довести, що вимірність дорівнює n треба знайти принаймні одну лінійно незалежну систему векторів, що містить n-векторів.
Такою системою векторів є наприклад:
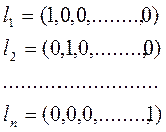
Доведемо, що вони лінійно незалежні. Складемо рівність (*).
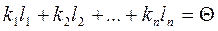 (*)
(*)
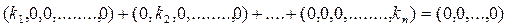
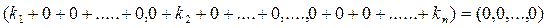
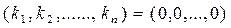
З цього випливає
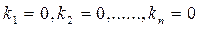
Тобто (*) виконується лише один раз при 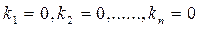 , тому система векторів є лінійно незалежною.
, тому система векторів є лінійно незалежною.
Отже, ми довели, що арифметичний простір є n-вимірним (n – кількість компонент вектора).
Зауваження. Поняття вимірності лінійного простору можна ввести і за таким означенням.
Означення. Вимірністю лінійного простору називається кількість векторів, що входять до базису.
Для того щоб це означення було корректним треба було б довести, що усі базиси даного простору містять однакову кількість векторів (насправді, це так).
Позначимо n-вимірний довільний векторний простір через Vn.
Введемо поняття підпростору даного простору Vn.
Означення. Підмножина 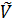 лінійного простору Vn називається підпростором даного простору, якщо
лінійного простору Vn називається підпростором даного простору, якщо 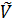 є само простором відносно операцій, визначених в Vn.
є само простором відносно операцій, визначених в Vn.
Безпосередньо з означення лінійного простору випливає, що для того щоб переконатися, що підмножина 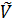 є підпростором, треба перевірити виконання десятьох умов. Дві з них стосуються визначеності операцій (додавання та множення на число), 8 умов – аксіоми, і описують властивості цих операцій. Насправді, треба перевірити виконання лише двох умов, а саме, визначеність операцій в
є підпростором, треба перевірити виконання десятьох умов. Дві з них стосуються визначеності операцій (додавання та множення на число), 8 умов – аксіоми, і описують властивості цих операцій. Насправді, треба перевірити виконання лише двох умов, а саме, визначеність операцій в 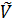 .
.
Доведемо це. Нехай в 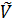 визначені ті ж операції що і в Vn, тобто:
визначені ті ж операції що і в Vn, тобто:
Якщо 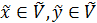 ,то
,то
а) 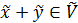 ;
;
б) 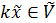 .
.
Зрозуміло, оскільки всі елементи множини 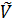 належать Vn, то з цього негайно випливає виконання аксіом 1), 2), 5), 6), 7), 8).
належать Vn, то з цього негайно випливає виконання аксіом 1), 2), 5), 6), 7), 8).
Доведемо, що виконується умова – аксіома 3), 4), тобто що 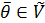 . Наспправді, нехай
. Наспправді, нехай 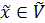 , оскільки
, оскільки 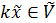 , то при
, то при 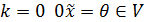 , а при
, а при 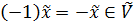 .
.
________________________________________________
Властивість 1. Визначник не зміниться, якщо його рядки зробити відповідними стовпцями.
Розглянемо визначник d.
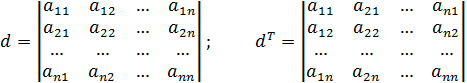
Стверджується, що 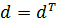
Розглянемо загальний член визначника d:
(1) 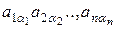 – загальний член d.
– загальний член d.
α1,α2,…,αn - перестановка з 1,2,…,n
Запишемо член (1) в позначках ij.
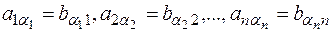
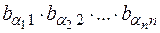 (1)
(1)
Таким чином (1) є членом і визначника d1. З′ясуємо, з яким знаком (1) входить до визначника d1. Знак члена (1) в d визначається парністю підстановки
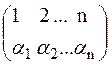
Знак (1) в d1 визначається парністю підстановки
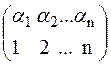
Ці підстановки, взагалі кажучи, різні, але парності в них однакові, тому що загальна кількість інверсій верхньої і нижньої перестановок однакова, тому і знаки члена (1) в d і d1 однакові.
Це перетворення, при якому всі рядки стають відповідними стовбцями, називається транспонуванням.
Властивість 2. Якщо в визначнику поміняти місцями будь які 2 рядки, то знак визначника зміниться на протилежний.
Доведення за схемою властивості 1.
Насправді, нехай у визначнику 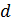 міняються місцями i-ий та j-ий рядки,
міняються місцями i-ий та j-ий рядки, 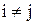 , а всі інші рядки залишаються на місці. Ми отримаємо визначник
, а всі інші рядки залишаються на місці. Ми отримаємо визначник 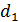 :
:
 .
.
Якщо 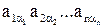 (1) є членом визначника
(1) є членом визначника 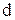 , то всі його елементи і у визначнику
, то всі його елементи і у визначнику 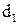 залишаються, очевидно, в різних рядках і різних стовпцях. Таким чином, визначники d та d1 складаються з одних і тих же членів.
залишаються, очевидно, в різних рядках і різних стовпцях. Таким чином, визначники d та d1 складаються з одних і тих же членів.
Члену (1) у визначнику 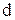 відповідає підстановка
відповідає підстановка 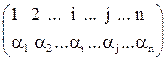 (2),
(2),
а у визначнику 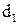 - підстановка
- підстановка 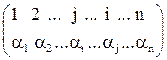 (3).
(3).
Підстановку (2) можна одержати з підстановки (1) однією транспозицією в верхньому рядку, тобто вона має протилежну парність. Звідси випливає, що всі члени визначника d входять до визначника d1 і відрізняються лише знаком.
Властивість 3. Якщо в визначнику є нульовий рядок, то визначник дорівнює 0.
Нехай усі елементи і-го рядка визначника є нулями
За означенням визначник n-го порядку це алгебраїчна сума n доданків, кожний з яких є добутком n елементів, узятих по одному з кожного рядка й кожного стовпця матриці і т.д. Отже, у кожний член визначника повинен увійти множником один елемент з і-ого рядка, тому в нашому випадку всі члени визначника дорівнюють нулю. Що й треба було довести.
Властивість 4. Якщо в визначнику є 2 рівних рядка, то визначник дорівнює 0.
Доведення. Нехай у визначнику d рівні між собою і-рядок і j=рядок
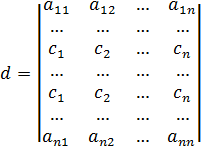
Нехай d = k
d1 – визначник d, в якому поміняли і з j рядок.
Тоді за властивістю 2:
d1=-k
Але насправді нічого не змінилось, оскільки, i та j рядки рівні
d1=d=k ⟹ -k=k
Звідси, 2k=0, k=0.
Властивість 5. Якщо всі елементи деякого рядка помножити на число r, то визначник зміниться в r разів.
Доведення за схемою властивості 1.
Цю ж властивість можна сформулювати у вигляді: якщо рядок визначника містить постійний множник, то його можна винести за знак визначника.
Розглянемо визначник d:
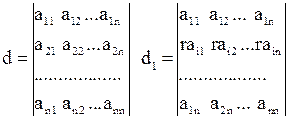
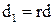
Нехай на r помножені всі елементи і-ого рядка. Кожний член визначника містить рівно один елемент із і-ого рядка, тому всілякий член отримує множник r, тобто сам визначник множиться на r.
Властивість 6. Якщо у визначнику є два пропорційні рядки, то визначник = 0.
Доведення проводиться з використанням властивості 5 і властивості 4.
Насправді, нехай елементи j-ого рядка визначника відмінюються від відповідних елементів і-ого рядка 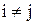 одним і тим самим множником r.
одним і тим самим множником r.
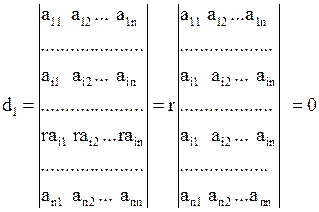
Виносячи спільний множник r із j-ого рядка за знак визначника, ми отримуємо визначник з двома однаковими рядками, який дорівнює нулю за властивістю 4.
Властивість 4 (а також властивість 3 при 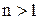 ) є, очевидно, окремим випадком властивості 6 (при r = 1 і r = 0).
) є, очевидно, окремим випадком властивості 6 (при r = 1 і r = 0).
Властивість 7. Якщо кожний елемент і-рядка визначників є сумою 2-ох доданків, то такий визначник можна подати як суму двох визначників, у яких всі рядки, за винятком і-ого такі ж, як у початковому. і-й рядок першого визначника складається з перших доданків, і-ий рядок другого визначника складається з других доданків.
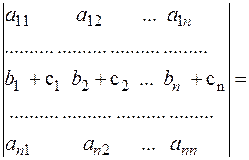
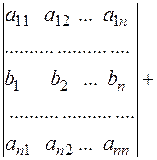
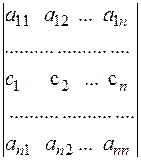
Доведення за схемою доведення властивості 1.
Дійсно, всілякий член заданого визначника можна подати у вигляді:
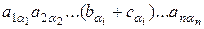
Збираючи разом перші доданки цих сум (з тими ж знаками, які мали відповідні члени в заданому визначнику) ми отримаємо, очевидно, визначник n-го порядку, що відмінюється від заданого визначника лише тим, що в і-ому рядку замість елементів 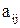 стоять елементи
стоять елементи 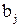 . Відповідно другі доданки складають визначник, в і-ому рядку якого стоять елементи
. Відповідно другі доданки складають визначник, в і-ому рядку якого стоять елементи 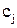 .
.
Властивість 8. Якщо до і-ого рядка визначника додати j-ий рядок, в подумках помножений на деяке число, то визначник не зміниться.
Доведення. Нехай до і-го рядка визначника d додається j-ий рядок, помножений на k, тобто в новому визначнику всілякий елемент і-го рядка має вигляд 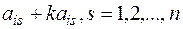 . Тоді на підставі властивості 7 цей визначник дорівнює сумі двох визначників, з яких перший є d, а другий містить пропорційні рядки і тому дорівнює 0.
. Тоді на підставі властивості 7 цей визначник дорівнює сумі двох визначників, з яких перший є d, а другий містить пропорційні рядки і тому дорівнює 0.
Властивість 9. Якщо в визначнику присутній рядок, що є лінійною комбінацією інших рядків, то визначник дорівнює 0.
Доведення.
Нехай, наприклад, і-ий рядок буде лінійною комбінацією s інших рядків
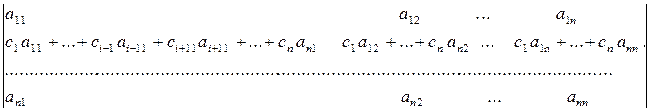
Застосовуючи властивість 7, ми подамо наш визначник у вигляді суми визначників, у кожному з яких і-ий рядок буде пропорційним до одного з інших рядків.
За властивістю 6 усі ці визначники дорівнюють нулю, дорівнює нулю, отже і заданий визначник теж.
Ця властивість є узагальненням властивості 6, причому вона дає найзагальніший випадок рівності визначника нулю.
___________________________________________________
Теорема Лапласа. Якщо в визначнику d виділити k рядків, то визначник d дорівнює сумі добутків всіляких мінорів k-го порядку, розташованих в цих k рядках, на їх алгебраїчні доповнення.
Доведення.
Нехай задано визначник d.
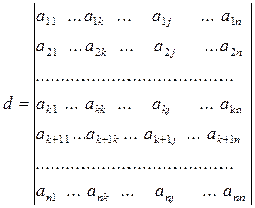
Для визначеності проведемо доведення, виділивши перші k рядків. Складемо всілякі мінори k-го порядку, що знаходяться у перших k рядках. Нехай це будуть мінори М1,М2,…,Мs. Побудуємо до кожного з мінорів його алгебраїчне доповнення. Треба довести, що d = M1A1+M2A2+…+MsAs.
Для доведення рівності доведемо 2 факти: кожний член d належить правій частині, і навпаки, кожний член правої частини є членом лівої частини. Другий факт безпосередньо випливає з леми про добуток мінору на його алгебраїчне доповнення. Доведемо перше. Візьмемо загальний член визначника d.
а1α1.а2α2…аkαk∙аk+1αk+1.аk+2αk+2…аnαn, де α1,α2,…,αn - перестановка з 1,2,…,n
Розіб'ємо загальний член на дві частини 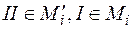 . Таким чином, ми довели, що а1α1.а2α2…аkαk∙аk+1αk+1.аk+2αk+2…аnαn
. Таким чином, ми довели, що а1α1.а2α2…аkαk∙аk+1αk+1.аk+2αk+2…аnαn 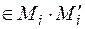
Для того, щоб збігались знаки розглянутого члена в d з М∙М', треба  замінити А1 (це випливає з леми). Таким чином, перший факт також доведений.
замінити А1 (це випливає з леми). Таким чином, перший факт також доведений.
Наслідок. Визначник дорівнює сумі добутків елементів будь-якого рядка на їх алгебраїчні доповнення.
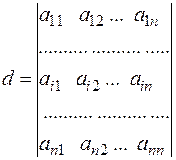
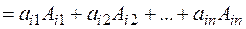
Нехай в теоремі Лапласа k=1.
Виділимо і-ий рядок. Тоді мінорами І порядку, розташованими в цьому рядку, будуть елементи цього рядка.
З цього наслідку випливає, що обчислення визначника n-го порядку зводиться до обчислення n визначників (n-1)-го порядку. Користуючись властивістю 8) визначників можна звести обчислення визначника n-го порядку до обчислення лише одного визначника (n-1)-го порядку.
Для цього доведемо, що в будь-якому рядку (якщо не всі елементи рядка нулі) за допомогою властивості 8) можна отримати всі нулі, крім одного.
Нехай 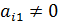 . Зробимо такі перетворення. До другого стовпця додамо перший, помножений на
. Зробимо такі перетворення. До другого стовпця додамо перший, помножений на 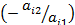 , …, до n-стовпця – перший помножений на
, …, до n-стовпця – перший помножений на 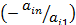 . Тоді отримаємо
. Тоді отримаємо
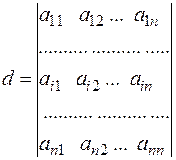
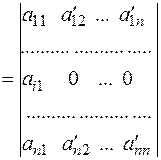
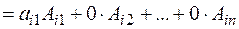
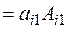
Таким чином, обчислення визначника n-го порядку зведено попереднім перетворенням до обчислення визначника (n-1)-го порядку
________________________________________________________
Теорема Крамера. Нехай задано систему n алгебраїчних рівнянь з n невідомими, визначник якої не нульовий. Тоді невідома xk дорівнює дробу, знаменником якого є визначник системи, а чисельником також є визначник, який можна отримати з визначника системи заміною k-го стовпця стовпцем вільних членів.
Доведення. Розглянемо систему
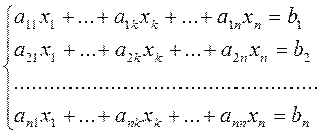 (1)
(1)
з визначником системи
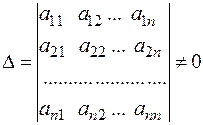 (2)
(2)
Помножимо обидві частини 1-го рівняння на А1k, 2-го на А2k, n-го на Аnk.
Тоді отримаємо
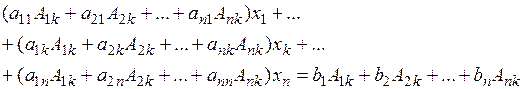
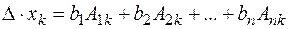 k=1,2,…,n (3)
k=1,2,…,n (3)
Введемо в розгляд деякий визначник.
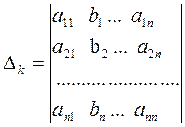
Застосуємо до k-го рядка цього визначника наслідок теореми Лапласа
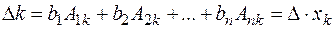
Застосуємо лему, тоді з рівності (3) маємо
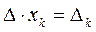
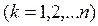
Отже
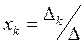
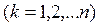
Теорему Крамера доведено.
___________________________________________
Властивість (транзитивності)
Якщо система векторів (1) лінійно виражається через систему векторів (2), а система (2) через систему (3), тоді система (1) лінійно виражається через (3).
Доведення.
Для зручності доведення цієї властивості введемо символ 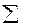 .
.
Нехай задано суму однотипних доданків
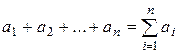
Застосовуючи двічі цей символ, отримаєм для
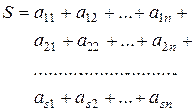
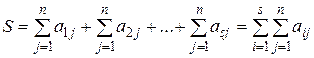
Доведемо таку властивість: 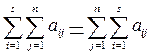
Для цього доведемо, що 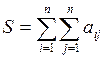 . Для доведення проведемо підсумування за стовпцями
. Для доведення проведемо підсумування за стовпцями
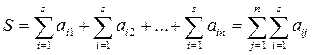
Отже
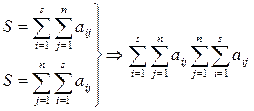
Тепер перейдемо до доведення попередньої властивості транзитивності.
Нехай задано системи:
|
|
|
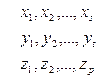
За умовою (1) лінійно виражається через (2). Тоді за означенням 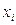 - є лінійною комбінацією векторів системи (2)
- є лінійною комбінацією векторів системи (2)
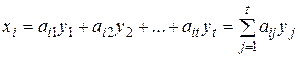 (i=1,2,…,S) (4)
(i=1,2,…,S) (4)
За умовою (2) лінійно виражається через (3), тому
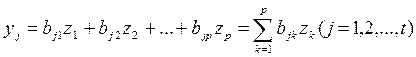
Підставимо (5) в (4), тоді отримаємо
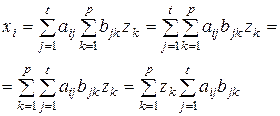
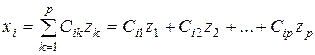
Отже доведено, що система векторів (1) лінійно виражається через систему (3).
Наслідок. Якщо система векторів (1) еквівалентна системі (2), а система (2) еквівалентна системі (3), то системи (1) і (3) еквівалентні.
Транзитивність еквівалентних систем доводиться повторенням двічі наведених міркувань.
 2020-09-24
2020-09-24 178
178






