Перестановки.
Перестановкой из n элементов называется любой упорядоченный набор из этих элементов.
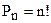 -число перестановок из n элементов
-число перестановок из n элементов
Объяснение: первый элемент можно выбрать n способами, второй – n-1 и т.д. последний элемент – одним способом, а перемножаются они исходя из правила обобщённого умножения.
Размещения.
Размещением из n по m называется любой упорядоченный набор из m элементов выбранных случайным образом из генеральной совокупности, содержащей n элементов (m<=n).
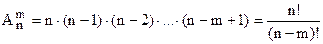 - число размещений из n элементов по m (число вариантов такого упорядоченного выбора).
- число размещений из n элементов по m (число вариантов такого упорядоченного выбора).
Объяснение: первый элемент можно выбрать n способами, второй – n-1 и т.д., а перемножаются они исходя из правила обобщённого умножения.
Сочетания.
Сочетанием из n по m называется любой неупорядоченный набор из m элементов выбранных случайным образом из генеральной совокупности, содержащей n элементов.
Сочетания и размещения связаны следующим образом:
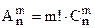 (на каждый состав из m элементов мы имеем m! упорядоченных наборов). Таким образом,
(на каждый состав из m элементов мы имеем m! упорядоченных наборов). Таким образом,
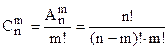 число сочетаний из n элементов по m (число вариантов такого не упорядоченного выбора).
число сочетаний из n элементов по m (число вариантов такого не упорядоченного выбора).
Размещения с повторениями
Размещением из n по m c повторениями называется любой упорядоченный набор из m элементов выбранных случайным образом из генеральной совокупности, содержащей n элементов, если выбор производится с возвращением.
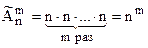 число размещений с повторениями из n элементов по m (число вариантов такого упорядоченного выбора).
число размещений с повторениями из n элементов по m (число вариантов такого упорядоченного выбора).
Объяснение: первый элемент можно выбрать n способами, второй – n и т.д., а перемножаются они исходя из правила обобщённого умножения.
Перестановки с повторениями
Пусть имеются n элементов, причём среди них есть одинаковые (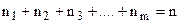 , ni –численности групп одинаковых элементов). Тогда число перестановок из этих элементов вычисляется по формуле:
, ni –численности групп одинаковых элементов). Тогда число перестановок из этих элементов вычисляется по формуле:
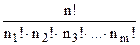
Знаменатель указывает на то, что при перестановке одинаковых элементов между собой сама перестановка не меняется.
Разбиение на группы
Пусть имеются n элементов, их надо разбить на m групп так чтобы 1 группа содержала n1 элементов, вторая – n2 и т.д. ….m-я группа nm, причём 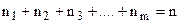
Тогда число способов осуществить это разбиение на группы рассчитывается по формуле:
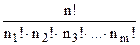


 Сочетания из 3 элементов по 2
Сочетания из 3 элементов по 2
(число неупорядоченных наборов из 3 элементов по 2 = 3)
 | |||||
 | |||||
 | |||||
 |  |
 (Общая формула
(Общая формула 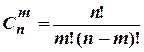 )
)
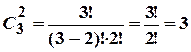
 | |||||||
 | |||||||
 | |||||||
 | |||||||
1).
 | ||||||||
 | ||||||||
 | ||||||||
| ||||||||
 | ||||||||
 2).
2).
 | ||||||||
 | ||||||||
 |  | |||||||
 | ||||||||
3).
 |


 Размещения из 3 элементов по 2
Размещения из 3 элементов по 2
(число упорядоченных наборов из 3 элементов по 2)=6
| ||||||
 |  | |||||
 |  | ||||
 | |||||
(Общая формула 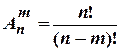 ) 1 2
) 1 2
 |
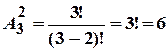
 | |||
 | |||
1).




2).
|
 3).
3).
 |
4).
 |


 5).
5).
6).



 | |||||
 | |||||
 | |||||
1)
 | ||||||||||
 | ||||||||||
 | ||||||||||
 | ||||||||||
 | ||||||||||
 | ||||||||||
 | ||||||||||
2)
 |
3).












4).
5).
6).
И т.д.
 2020-09-24
2020-09-24 69
69






