2020-10-10
103Рис. 2-4
Сложение
Вычитание
Преобразования Галилея:
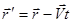
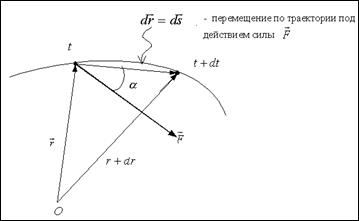
Рис. 2-9
Скалярное произведение
Работа силы 
на перемещении 
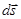производится проекцией силы на это направление 
: 
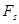- скалярное произведение.
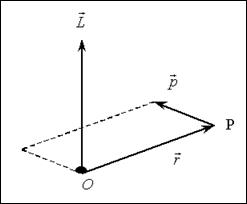
Рис. 3-7
Векторное произведение-направление есть вывинчивание правого винта (от r к p)
Моментом количества движения частицы (материальной точки) P относительно некоторой точки 
называется вектор 
, 
Рис. 1-2
Координаты события:
Положение точки: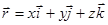 
, расстояние между точками 1 и 2: 
.
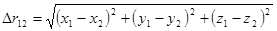См. Рис. 2-4
Мгновенная и средняя скорость
= 
.
Мгновенное ускорение 
.
Система 
вращается с постоянной угловой скоростью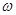 
вокруг оси, неподвижной в системе 
:
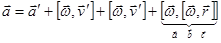
правило «бац-цаб»
Сложение векторов 
| Умножение векторов  =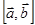 
|
| x3=x1+x2 | x3=y1z2-z1y2 |
| y3=y1+y2 | y3=z1x2-x1z2 |
| z3=z1+z2 | z3=x1y2-y1x2 |
Движение по окружности
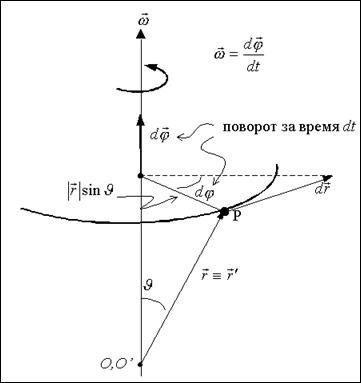
Рис. 3-2
Псевдовектор
Угловая скорость:
направление есть ввинчивание правого винта (направление dr есть вывинчивание, т.е. вверх!)
|
|
|
Связь с линейными характеристиками:
Изменение скорости и ускорения
, - 
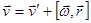
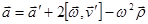- осестремительное ускорение, нормальное!
- кориол и сово ускорение, тангенциальное.
Дифференцирование и интегрирование
Определение:
производная функции f(x) по x: 
Смысл –угловой коэффициент касательной к f(x) в т. x
Вектор мгновенной скорости и производная:
= 
=
= 
В итоге: три производные от координат!
Определенный интеграл от f(x) в пределах от a до b есть предел интегральной суммы при разбиении промежутка [ ab ] на малые промежутки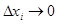 
, т. е.
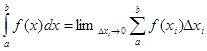Имеет смысл площади под f(x) на [ ab ].
Рис. 2-10
Работа силы на траектории 
между точками 1 и 2 равна сумме работ на элементарных отрезках:
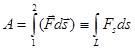
- криволинейный интеграл по .
Конец Напоминания.
Проблема движения планет
Воспользуемся полученной информацией для рассмотрения проблемы движения планет Солнечной системы.
РИС. 3-11
Радиус орбиты движения Земли (T) вокруг Солнца (S)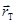 
»150000000 км.
Если пренебречь взаимодействием между планетами,
задача сводится к проблеме движения материальной точки в поле центральных сил.
Введем понятие секториальной скорости.
Пусть в момент времени t положение точки определяется радиусом-вектором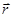 
, через промежуток времени 
- радиусом-вектором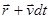 
.
РИС. 3-12
Величине 
придается векторный смысл, чтобы зафиксировать направление движения. Площадь, ометаемая радиусом-вектором точки, движущейся вокруг силового центра О, за время : 
.
|
|
|
Скорость изменения площади, ометаемой радиусом-вектором (секториальная скорость): 
.
По определению момента количества движения 
.
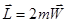- в случае движения материальной точки в центральном поле ее момент количества движения пропорционален ее секториальной скорости.
Два следствия
1) Постоянство вектора – это постоянство не только его абсолютного значения (модуля), но и его направления. Значит, плоскость, перпендикулярная 
, занимает постоянное положение в пространстве; именно в этой плоскости лежат вектора 
и 
. Следовательно, траектория движения материальной точки в поле центральных сил – это плоская кривая.
1-ый закон Кеплера (1609 год)
В невозмущенном движении, т.е. в задаче двух тел, орбита движущейся точки есть плоская кривая второго порядка, в одном из фокусов которой находится центр силы притяжения.
Планеты движутся вокруг Солнца по эллипсам, в одном из фокусов которых находится Солнце.
2) Из постоянства модуля вектора 
следует, что в равные времена радиус-вектор материальной точки, движущейся в поле центральных сил, ометает равные площади.
РИС. 3-13
2-ой закон Кеплера (1609 год)
В невозмущенном движении площадь, описываемая радиусом-вектором точки, движущейся в поле центральных сил, изменяется пропорционально времени.
Радиус-вектор планеты за равные промежутки времени описывает равные площади.
Оба эти закона Кеплера были в свое время получены в результате обработки экспериментальных данных Тихо Браге (1546-1601) и привели впоследствии Ньютона к установлению закона всемирного тяготения: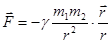 
- всегда притяжение – единственная сила, управляющая движением астрономических тел.
3-ий закон Кеплера (1619 год).
Формулировка Кеплера:
квадраты времен обращений планет относятся как кубы больших осей эллиптических орбит, по которым они движутся вокруг Солнца: 
Справедливость 3-го закона Кеплера можно доказать, если считать орбиты планет круговыми. Это предположение не слишком грубое, так как эксцентриситет орбит планет невелик: для орбиты Земли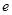 
»0.017, для орбиты Меркурия 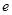»0.205.
Напоминание
Эксцентриситет кривой второго порядка (конического сечения) – число, равное отношению расстояния от любой точки кривой 2-го порядка до фокуса к расстоянию от этой точки до соответствующей директрисы.
РИС. 3-14
У эллипса две директрисы (
), каждая соответствует своему фокусу 
; эксцентриситет: 
. Уравнение директрис: 
; 
. Если 
, то 
и эллипс вырождается в прямую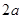 
. Если 
, то директриса удаляется в бесконечность, фокусы сливаются в один. Эллипс превращается в окружность.
Итак, малость эксцентриситетов орбит планет Солнечной системы позволяет считать их орбиты круговыми.
Пусть одна планета имеет массу 
, круговую орбиту радиуса 
и период обращения 
, вторая планета - 
.
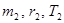Стационарное состояние: центробежная сила равна и противоположно направлена силе притяжения:
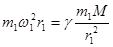, где 
- масса Солнца,
Гравитационная постоянная g =6,6710-11 м3/кгс2 или
(6.6732±0.0031)× 10-8 дин×см2/г2 [Н×м2/кг2].
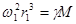- универсальная константа.
Заменяя 
, находим:
или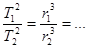 
Для планет, движущихся по круговым орбитам, 3-ий закон Кеплера:
Мы знаем, что ускорение материальной точки (планеты) при равномерном движении по круговой орбите:
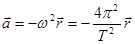. Подставим следующее обозначение: 
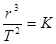(постоянная Кеплера); 
; тогда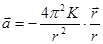 
и соответственно сила 
.
Поскольку планета и Солнце равноправно должны входить в закон взаимодействия:
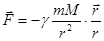, где - масса Солнца. Из сравнения сил видно, что
постоянная Кеплера 
.
Ньютон не объяснил происхождения гравитационного взаимодействия – одной из фундаментальных сил природы. Общая теория относительности тоже не дает какого-либо наглядного толкования тяготения, дает лишь новый способ описания и более глубокое обобщение закона всемирного тяготения.
|
|
|
4 Лекция 4
