Квадратная решетка, координатная плоскость

В данной теме захватывается большой спектр задач, связанных с вычислением углов, 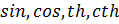 углов, площадей различных фигур, изображенных на квадратной решетке или на координатной прямой.

В данной главе мы постараемся разобрать наиболее часто встречающиеся задачи и обобщить список формул необходимых для их решения.

Итак, начнем с задач на нахождение углов и 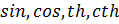 углов изображенных на квадратной решетке.

Для решения данного типа задач необходимо помнить ряд формул и правил:

1) Синусом острого угла в прямоугольном треугольнике называют отношение противолежащего катета к гипотенузе.

2) Косинусом острого угла в прямоугольном треугольнике называют отношение прилежащего катета к гипотенузе.

3) Тангенсом острого угла в прямоугольном треугольнике называют отношение противолежащего катета к прилежащему катету.

4) Котангенсом острого угла в прямоугольном треугольнике называют отношение прилежащего катета к противолежащему катету.

Например.

На клетчатой бумаге с размером клетки 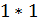 изображён угол 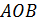. Найдите тангенс этого угла. Ответ округлите до целого числа.

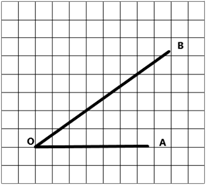
Для этого необходимо достроить данный угол до прямоугольного треугольника:

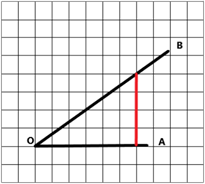
Далее необходимо по правилу найти тангенс острого угла 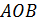 в треугольнике .

.

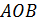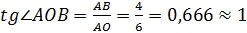Ответ: 1.

Также необходимо помнить формулы приведения для вычисления тупых углов. Приведем некоторые из них:

1)

2)

3)

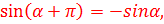
4)

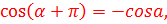
5)

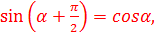
6)

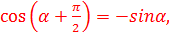
7)

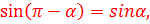
8)

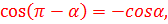
9)

10)

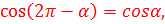
11)

12)

13)

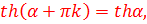
14)

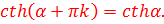
Следующий тип задач, связан с нахождением длины медианы, биссектрисы, высоты в треугольнике изображенном на клетчатой бумаге.

Для этого полезно помнить, что:

1) Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

2) Биссектриса треугольника - это луч, делящий угол на две равные части (пополам).

3) Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне или продолжению противоположной стороны.

Например.

На клетчатой бумаге с размером клетки 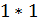 изображён треугольник ABC. Найдите длину высоты треугольника, опущенной из вершины .

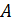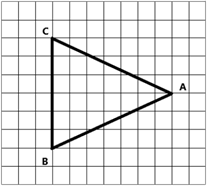
Решение.

Для начала опустим высоту из вершины :

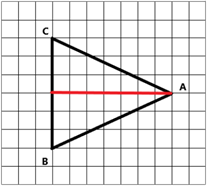
По рисунку определим длину высоты в клетках. Получаем, что высота равна 7.

Ответ: 7.

Например.

На клетчатой бумаге с размером клетки 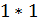 изображён параллелограмм. Найдите длину его большей высоты.

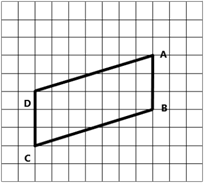
Для начала построим высоты и определим по рисунку большую из высот:

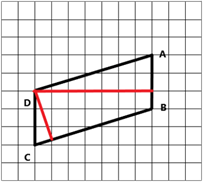
По рисунку видно, что высота опущенная из вершины 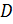 к стороне  является большей. Найдем ее длину, посчитав клеточки на рисунке. Получаем, что длина большей высоты равна 7.

Ответ: 7.