Изучение
Физического маятника
Выполнили:
студенты группы Ф–14
Кукобникова В.В.,
Лобан А.А.
Цель работы: Исследование законов колебательного движения физического маятника и определение ускорения свободного падения.
Приборы и принадлежности: установка FPM-04, линейка.
Краткие теоретические сведения
Физическим маятником (ФМ) называется твёрдое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси. Точка О пересечения этой оси с вертикальной плоскостью, проходящей через центр масс маятника, называется точкой подвеса.
Согласно основному уравнению динамики вращательного движения, в отсутствии сил сопротивления, уравнение движения ФМ имеет вид:
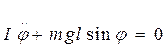 (1)
(1)
где I - момент инерции маятника относительно оси качания, 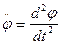 - угловое ускорение маятника, m - масса маятника, l - расстояние от точки подвеса до центра масс маятника.
- угловое ускорение маятника, m - масса маятника, l - расстояние от точки подвеса до центра масс маятника.
Ограничиваясь, случаем малых углов (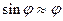 ) из (1) имеем:
) из (1) имеем:
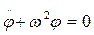 (2)
(2)
где введено обозначение 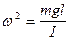
Нетрудно убедится, что решением записанного дифференциального уравнения (2) является функция:
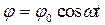
т.е. угол j отклонения ФМ от вертикали изменяется по гармоническому закону. Следовательно, период колебаний ФМ равен:
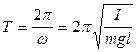 (3)
(3)
Как известно, период математического маятника:
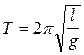 (4)
(4)
Сравнивая (3) и (4) находим, что ФМ колеблется с тем же периодом, что и математический, имеющий длину:
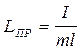 (5)
(5)
Длина математического маятника 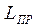 , имеющего тот же период колебаний, что и данный ФМ, называется приведённой длиной физического маятника.
, имеющего тот же период колебаний, что и данный ФМ, называется приведённой длиной физического маятника.
Точка 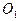 , лежащая на прямой, соединяющей точку подвеса и центр тяжести с ФМ, на расстоянии
, лежащая на прямой, соединяющей точку подвеса и центр тяжести с ФМ, на расстоянии 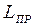 от точки подвеса, называется центром качаний ФМ.
от точки подвеса, называется центром качаний ФМ.
Точка подвеса О и центр качаний 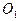 ФМ принято называть взаимными точками ФМ, так как они обладают следующим свойством: если перенести точку подвеса маятника в центр качаний, то прежняя точка подвеса станет центром качаний, причём период колебаний ФМ при этом не изменяется.
ФМ принято называть взаимными точками ФМ, так как они обладают следующим свойством: если перенести точку подвеса маятника в центр качаний, то прежняя точка подвеса станет центром качаний, причём период колебаний ФМ при этом не изменяется.
Экспериментальная проверка формул (4) и (5) составляет одну из задач данной работы.
Получим формулы (4) и (5) для ФМ, выполненного в виде тонкого однородного стержня массой m и длины l. Момент инерции тонкого стержня относительно оси, проходящей через центр масс С перпендикулярно плоскости рисунка, равен 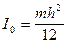 . По теореме Штейнера находим, что момент инерции стержня относительно оси качаний:
. По теореме Штейнера находим, что момент инерции стержня относительно оси качаний:
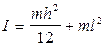 (6)
(6)
Подставим (6) в (4) и (5), приходим к соотношению:
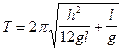 (7)
(7)
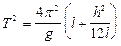 (8)
(8)
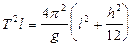 (9)
(9)
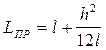 (10)
(10)
Соотношение удобно для анализа и экспериментальной проверки. В частности, из анализа на экстремум функции (7) следует, что при:
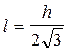 (11)
(11)
Период Т физического маятника является минимальным.
Выполнение работы
Упражнение 1
Проверка формулы периода колебаний иопределение приведённой длины физического маятника.
1) Определяем время t 10- 15 полных колебаний стержня. Результаты измерений заносим в таблицу 1 и определяем 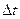 .
.
Таблица 1
| № | N | t, (с) | T, (с) | h, (м) | l, (м) | Lпр, (м) |
| 1 | 10 | 12,11 | - | 0,6 | 0,24 | 0,365 |
| 2 | 10 | 12,22 | ||||
| 3 | 10 | 12,16 | ||||
| 4 | 10 | 12,18 | ||||
| 5 | 10 | 12,91 | ||||
| Ср. знач. | 10 | 12,12 | 1,21 | - | - | - |
∆t = (12,12±0.0016) c.
2) По формуле 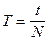 , где N- число полных колебаний стержня, рассчитываем период колебаний ФМ.
, где N- число полных колебаний стержня, рассчитываем период колебаний ФМ.
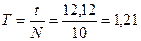 с.
с.
3) Измеряем длину стержня h и расстояние l от точки подвеса до центра тяжести, проверяем справедливость формулы (8).
 ;
; 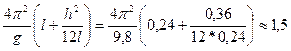 .
.
4) Пользуясь формулой (10) рассчитываем приведённую длину 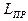 ФМ.
ФМ.
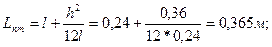
5) Повернув верхний кронштейн установки на  и установив длину математического маятника
и установив длину математического маятника 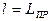 определяем период колебаний математического маятника. Результаты измерений заносим в таблицу 2.
определяем период колебаний математического маятника. Результаты измерений заносим в таблицу 2.
Таблица2
| № | N | t, (с) | Tмат, (с) |
| 1 | 10 | 11,26 | 1,15 |
| 2 | 10 | 11,61 | |
| 3 | 10 | 11,56 | |
| 4 | 10 | 11,91 | |
| 5 | 10 | 11,48 | |
| Ср. знач. | - | 11,56 | - |
6) Сравниваем периоды колебаний физического и математического маятников.
Периоды колебаний физического и математического маятника, длина которого является приведенной длиной данного физического маятника, равны.
Упражнение 2
Исследование формулы периода колебаний ФМ.
1) Последовательно увеличивая расстояние L на 10 мм, измеряем время t 10-15 полных колебаний. Результаты заносим в таблицу 3.
Таблица 3
| № | N | t1 | t2 | t3 | Ср.знач. t | l, (м) | T, (c) |
| 1 | 10 | 26,18 | 26,74 | 26,38 | 26,43 | 0,01 | 2,643 |
| 2 | 10 | 21,29 | 21,22 | 21,19 | 21,23 | 0,02 | 2,123 |
| 3 | 10 | 18,01 | 18,11 | 18,34 | 18,15 | 0,03 | 1,815 |
| 4 | 10 | 16,50 | 16,26 | 16,24 | 16,33 | 0,04 | 1,633 |
| 5 | 10 | 15,00 | 15,12 | 15,01 | 15,04 | 0,05 | 1,504 |
| 6 | 10 | 14,06 | 13,87 | 14,02 | 13,98 | 0,06 | 1,398 |
| 7 | 10 | 13,57 | 13,61 | 13,50 | 13,56 | 0,07 | 1,356 |
| 8 | 10 | 12,87 | 12,53 | 12,71 | 12,70 | 0,08 | 1,270 |
| 9 | 10 | 12,64 | 12,35 | 12,24 | 12,41 | 0,09 | 1,241 |
| 10 | 10 | 12,20 | 12,24 | 12,11 | 12,18 | 0,10 | 1,218 |
| 11 | 10 | 11,79 | 11,89 | 11,81 | 11,83 | 0,11 | 1,183 |
| 12 | 10 | 11,70 | 11,73 | 11,90 | 11,78 | 0,12 | 1,178 |
| 13 | 10 | 11,64 | 11,55 | 11,50 | 11,56 | 0,13 | 1,156 |
| 14 | 10 | 11,50 | 11,37 | 11,46 | 11,44 | 0,14 | 1,144 |
| 15 | 10 | 11,48 | 11,29 | 11,34 | 11,37 | 0,15 | 1,137 |
| 16 | 10 | 11,40 | 11,38 | 11,21 | 11,33 | 0,16 | 1,133 |
| 17 | 10 | 11,43 | 11,53 | 11,23 | 11,40 | 0,17 | 1,140 |
| 18 | 10 | 11,30 | 11,71 | 11,24 | 11,42 | 0,18 | 1,142 |
2) По результатам таблицы 2 строим график зависимости T.
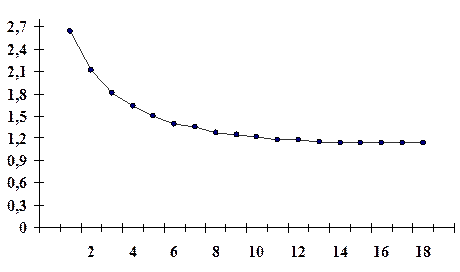 l, см
l, см
Поведение графика объясняется на основании формулы 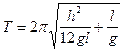 .
.
3) По данным таблицы 2 строим график зависимости 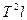 от
от 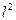 и убеждаемся, что она является линейной.
и убеждаемся, что она является линейной.
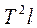
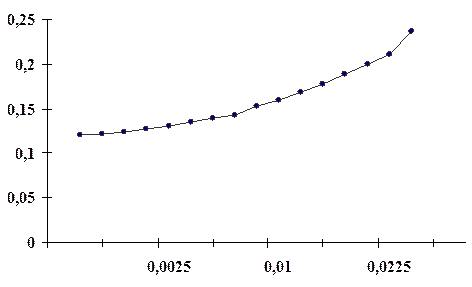
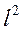 , м
, м
Вывод: исследовав законы колебательного движения физического маятника, определили, что время колебаний уменьшалось до определенного этапа, после чего оно опять стало увеличиваться; выяснили, что периоды колебаний физического и математического маятника, длина которого является приведенной длиной данного физического маятника, равны; период физического маятника не зависит от свойств вещества, из которого изготовлен ФМ, его массы, плотности, а определяется лишь расстоянием от точки подвеса до центра тяжести тела.
 2020-10-12
2020-10-12 165
165






