Z 1=r1+j(XL1–XC1)=3.5+j(4–11.5)=3.5-j7.5,
Z 2=r2–jXC2=4-j3,
Z 3=r3+jXL3=3+j4.
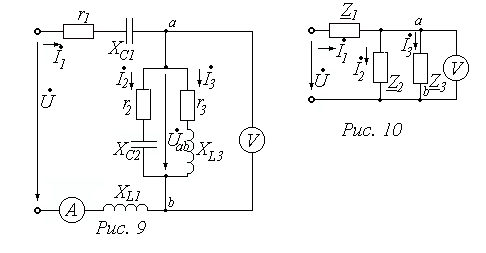 |
Определяем эквивалентное сопротивление параллельного участка a–b:
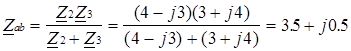
Комплексное входное сопротивление всей схемы
Z вх= Z 1+ Z ab=(3.5-j7.5)+(3.5+j0.5)=7-j7=7 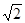 ×e-j45°
×e-j45°
Входной ток 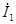
 |

Действующее значение тока
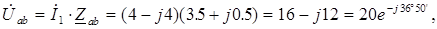
Определяем напряжение на зажимах a–b параллельного участка
вольтметр покажет V=|  |=20 B, а амперметр A=|
|=20 B, а амперметр A=| 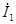 |=4
|=4 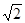 A.
A.

Токи в параллельных ветвях
Токи 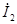 и
и 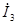 могут быть определены по формулам
могут быть определены по формулам
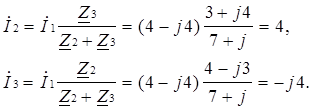
Вычислим активные и реактивные составляющие токов I2 и I3.
Угол сдвига фаз между напряжением  и током
и током 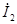 (он равен аргументу Z 2) равен j2=yuab–yi2=-36°50'–0=-36°50', а угол сдвига фаз между
(он равен аргументу Z 2) равен j2=yuab–yi2=-36°50'–0=-36°50', а угол сдвига фаз между  и
и 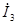
j3=yuab–yi3=-36°50'–(-90°)=53°10'.
Тогда активные составляющие токов I2 и I3
I2a=I2 cosj2=4×cos(-36°50')=4×0.8=3.2,
I3a=I3 cosj3=4×cos(53°10')=4×0.6=2.4.
Реактивные составляющие токов I2 и I3
I2р=I2 sinj2=4×sin(-36°50')=-4×0.6=-2.4,
I3р=I3 sinj3=4×sin(53°10')=4×0.8=3.2.
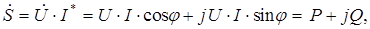
Наконец, определим полную, активную и реактивную мощности в схеме. Запишем мощность в комплексной форме:
где 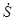 – полная мощность в комплексной форме;
– полная мощность в комплексной форме;
P=Re(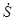 )=U×I×cosj – активная мощность;
)=U×I×cosj – активная мощность;
Q=Jm(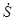 )=U×I×sinj – реактивная мощность;
)=U×I×sinj – реактивная мощность;
I* – комплексный ток, сопряженный с 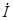 .
.
Таким образом, мощность источника
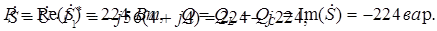
Следовательно,
Активная мощность, поступающая из источника, рассеивается в виде тепла в сопротивлениях резисторов схемы;
P=Pr1+Pr2+Pr3=I12r1+ I22r2+ I32r3=(4 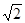 )2×3.5+42×4+42×3=224 Вт.
)2×3.5+42×4+42×3=224 Вт.
Активная мощность в резисторах r2 и r3 может быть определена и так:
Pr2=Uab×I2a=Uab×I2×cosj2=20×3.2=64 Вт;
Pr3=Uab×I3a=Uab×I3×cosj3=20×2.4=48 Вт.
Реактивную составляющую полной мощности можно определить также следующим образом:
Q=QL–QC=(I12XL1+I32XL3)–(I12XC1 +I22XC2)=[(4 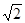 )2×4+42×4]–[(4
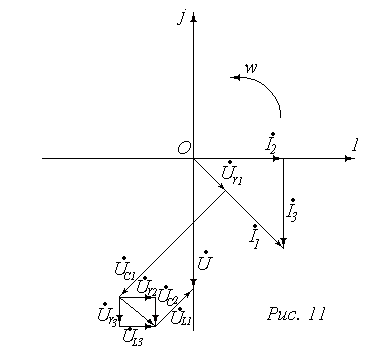
)2×4+42×4]–[(4 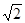 )2× 11.5+42×3]=-224 вар,
)2× 11.5+42×3]=-224 вар,
а для реактивных мощностей участка a–b
QC2=Uab×I2×sinj2=Uab×I2p=20(-2.4)=-48 вар,
QC3=Uab×I3×sinj3=Uab×I3p=20×3.2=64 вар.
Баланс мощностей выполняется.
На рис. 11 приведена векторная диаграмма токов, построенная в комплексной плоскости на основании первого закона
 |
Кирхгофа
 |
Для построения векторной диаграммы напряжений для любого контура (всей цепи) следует предварительно рассчитать напряжения на всех пассивных элементах и источниках токов схемы, задавшись их положительным направлением.
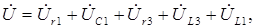
На рис. 11 приведена векторная диаграмма, построенная согласно уравнению по второму закону Кирхгофа
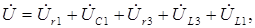 |
где
 =
= 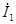 ×r1=(4-j4)×3.5=14-j14=14
×r1=(4-j4)×3.5=14-j14=14 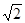 ×e-j45°;
×e-j45°;
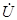 c1=
c1= 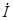 1×(-jXc1)=(4-j4)(-j11.5)=-46–j46=46
1×(-jXc1)=(4-j4)(-j11.5)=-46–j46=46 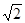 ×e-j135°;
×e-j135°;
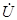 r3=
r3= 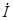 3×r3=-j4×3=-j12=12×e-j90°;
3×r3=-j4×3=-j12=12×e-j90°;
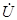 L3=
L3= 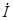 3×jXL3=-j4×j4=16=16×ej0°;
3×jXL3=-j4×j4=16=16×ej0°;
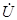 L1=
L1= 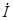 1×jXL1)=(4-j4)×j4=16+j16=16
1×jXL1)=(4-j4)×j4=16+j16=16  ×ej45°;
×ej45°;
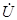 =-j56=56×e-j90°;
=-j56=56×e-j90°; 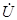 ab=
ab= 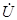 r3+
r3+ 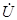 L3;
L3;
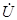 r2=
r2=  2×r2=4×4=16=16×ej0°;
2×r2=4×4=16=16×ej0°;
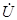 C2=
C2=  2×(-jXc2)=4×(-j3)=-j12=12×e-j90°;
2×(-jXc2)=4×(-j3)=-j12=12×e-j90°;
а напряжение на параллельных ветвях 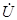 ab=
ab= 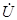 r2+
r2+ 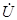 С2=16-j12.
С2=16-j12.
Построение начинаем, например, с вектора 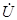 r1, который совпадает по направлению с током
r1, который совпадает по направлению с током  1. Вектор
1. Вектор 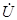 С1 отстает от вектора тока
С1 отстает от вектора тока  1 на угол 90°. Вектор напряжения
1 на угол 90°. Вектор напряжения 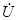 r3 совпадает с направлением тока
r3 совпадает с направлением тока  3 и т. д. Векторные диаграммы построены для комплексных действующих значений токов и напряжений (для комплексных амплитуд векторы должны быть умножены на
3 и т. д. Векторные диаграммы построены для комплексных действующих значений токов и напряжений (для комплексных амплитуд векторы должны быть умножены на  ).
).
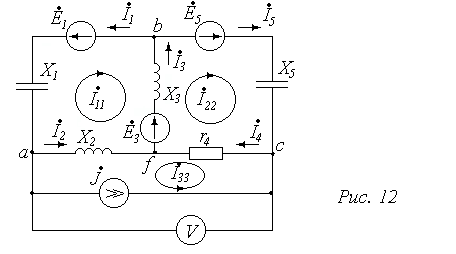
Пример 4. В схеме (рис. 12) заданы 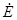 1=-j110 B,
1=-j110 B, 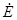 3=j10 B,
3=j10 B, 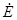 5=j20 B,
5=j20 B,  =40 A, X1=15 Ом, X2=5 Ом, X3=10 Ом, r4=4 Ом, X5=7 Ом. Определить все токи, показания амперметра и вольтметра электромагнитной системы. Составить баланс мощностей.
=40 A, X1=15 Ом, X2=5 Ом, X3=10 Ом, r4=4 Ом, X5=7 Ом. Определить все токи, показания амперметра и вольтметра электромагнитной системы. Составить баланс мощностей.
Решение. Воспользуемся методом контурных токов. Так как в схеме имеется ветвь с идеальным источником J, то в качестве одного из контурных выбираем ток, равный заданному источнику J. При этом должно выполняться условие: в данной ветви должен быть лишь один контурный ток – ток источника J.
С учетом этого выбираем систему независимых контуров с указанными на рис. 12 положительными направлениями контурных токов  11,
11,  22,
22,  33=
33=  =40 A.
=40 A.
Записываем систему уравнений в канонической форме. Система состоит из двух уравнений:

 11 Z 11+
11 Z 11+  22 Z 12+
22 Z 12+  33 Z 13=
33 Z 13= 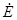 11,
11,
 11 Z 21+
11 Z 21+  22 Z 22+
22 Z 22+  33 Z 23=
33 Z 23= 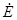 22,
22,
где собственные сопротивления первого и второго контуров равны:
Z 11= Z 1+ Z 2+ Z 3=-jX1+ jX2+ jX3=-j15+j5+j10=0 Ом,
Z 22= Z 4+ Z 3+ Z 5=r4+ jX3– jX5=4+j10–j7=4+j3 Ом,
а общие сопротивления ветвей, принадлежащих смежным контурам,
Z 12= Z 21=- Z 3=-jX3=-j10, Z 23= Z 4=r4=4,
Z 13= Z 31= Z 2=jX2=j5.
Знаки у сопротивлений обусловлены встречным направлением контурных токов  11 и
11 и  22 в сопротивлении Z 3 и одинаковым направлением
22 в сопротивлении Z 3 и одинаковым направлением  33 и
33 и  11,
11,  22 и
22 и  33 соответственно в сопротивлениях Z 2 и Z 4.
33 соответственно в сопротивлениях Z 2 и Z 4.
Контурные ЭДС
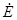 11=-
11=- 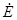 1–
1– 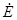 3=-(-j110)–j10=j100,
3=-(-j110)–j10=j100,
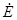 22=
22= 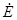 3+
3+ 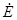 5=j10+j20=j30.
5=j10+j20=j30.
Решая систему уравнений
 11×0–
11×0–  22×j10+40×5=j100,
22×j10+40×5=j100,
-  11×j10+
11×j10+  22×(4+j3)+40×4=j30,
22×(4+j3)+40×4=j30,
находим контурные токи
 11=-j20,
11=-j20,  22=10, а
22=10, а  33=J=40.
33=J=40.
Комплексные токи в ветвях схемы указанных направлений (см. рис. 12) определяем, учитывая, что ток в ветви, принадлежащей одному контуру, равен контурному току с учетом знака; ток в ветви, принадлежащей нескольким контурам, равен алгебраической сумме контурных токов; в обоих случаях со знаком "плюс" берется контурный ток, направление которого совпадает с направлением искомого тока ветви.
Таким образом,
 1= -
1= -  11=j20,
11=j20,  2=-(
2=-(  11+
11+  33)=-40+j20,
33)=-40+j20,
 3=
3=  22–
22–  11=10+j20,
11=10+j20,  4=
4=  22+
22+  33=10+40=50,
33=10+40=50,  5=
5=  22=10.
22=10.
Мгновенные значения токов записываем, переходя от их комплексных действующих значений:
i1=20  ×sin(wt+90°),
×sin(wt+90°),
i2=20 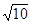 ×sin(wt+153°30'),
×sin(wt+153°30'),
i3=10 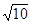 ×sin(wt+63°30'),
×sin(wt+63°30'),
i4=50  ×sin wt,
×sin wt,
i5=10  ×sin wt,
×sin wt,
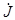 Û40
Û40  sin wt.
sin wt.
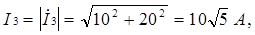 |
Амперметр А3 показывает действующее значение тока I3,
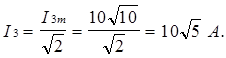
или
Определим напряжение на зажимах источника тока, выбрав его направление, например 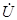 ca. Уравнение по второму закону может быть записано для любого контура, в который входит ветвь с источником тока.
ca. Уравнение по второму закону может быть записано для любого контура, в который входит ветвь с источником тока.
При обходе контура a–f–c–a по часовой стрелке получим уравнение
 2jX2–
2jX2–  4r4+
4r4+ 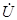 ca=0,
ca=0,
откуда
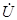 ca=
ca=  4r4–
4r4–  2jX2=50×4–(-40+j20)j5=300+j200 B.
2jX2=50×4–(-40+j20)j5=300+j200 B.
Вольтметр V, измеряющий действующее значение напряжения Uca, покажет
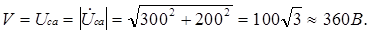
Баланс мощностей можно составить только для всей схемы, он служит для проверки правильности расчета.
Полная комплексная мощность источников должна быть равна полной комплексной мощности потребителей:
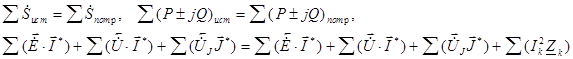
На схеме (см. рис. 12) 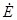 1 и
1 и  1,
1, 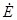 5 и
5 и  5,
5, 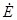 3 и
3 и  3 направлены в одну сторону и являются источниками энергии; напряжение
3 направлены в одну сторону и являются источниками энергии; напряжение  ca и ток
ca и ток 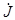 направлены встречно, т. е.
направлены встречно, т. е.  – источник энергии.
– источник энергии.
Таким образом
å 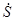 ист=
ист= 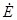 1I*1+
1I*1+ 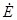 3I*3+
3I*3+ 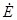 5I*5+
5I*5+  JJ*=(-j110)(-j20)+j10(10-j20)+j20×10+ (300+j200)40=10000+j8300.
JJ*=(-j110)(-j20)+j10(10-j20)+j20×10+ (300+j200)40=10000+j8300.
Pист=10000 Вт, Qист=8300 вар.
Потребителями являются все пассивные элементы схемы, потребляемую мощность которых можно посчитать так:
å 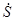 потр=å(Ik2 Z k),
потр=å(Ik2 Z k),
где Ik – действующие значения токов (модули);
Z k– комплексные сопротивления.
Тогда
å 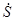 потр=I12 Z 1+ I22 Z 2+ I32 Z 3+ I42 Z 4+ I52 Z 5=202(-j15)+(20
потр=I12 Z 1+ I22 Z 2+ I32 Z 3+ I42 Z 4+ I52 Z 5=202(-j15)+(20  )2(j5)+ (10
)2(j5)+ (10  )2(j10)+ 502×4+102(-j7)=10000+j8300,
)2(j10)+ 502×4+102(-j7)=10000+j8300,
Pпотр=10000 Вт, Qпотр=8300 вар.
Баланс мощностей сходится.
Пример 5. В схеме (рис. 13) заданы: 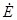 1=j110 B,,
1=j110 B,, 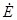 5=j80 B,
5=j80 B,  =3 A, X1'= X3=10 Ом, X2=40 Ом, X1"=r4=20 Ом, r6=30 Ом. Определить все токи методом узловых потенциалов и показания вольтметра.
=3 A, X1'= X3=10 Ом, X2=40 Ом, X1"=r4=20 Ом, r6=30 Ом. Определить все токи методом узловых потенциалов и показания вольтметра.
Решение. В схеме имеется ветвь с идеальной ЭДС 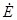 5. За базисный узел принимаем, например, узел d, т. е.
5. За базисный узел принимаем, например, узел d, т. е.  d=0. Тогда потенциал узла c равен величине
d=0. Тогда потенциал узла c равен величине 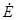 5 со знаком "плюс" (
5 со знаком "плюс" (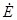 5 направлена к узлу с):
5 направлена к узлу с):
 с=j80.
с=j80.
 |
Записываем систему уравнений по методу узловых потенциалов для определения двух оставшихся неизвестных узлов a и b схемы:
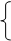 Y aa
Y aa  a+ Y ab
a+ Y ab  b+ Y ac
b+ Y ac  c=
c=  aa,
aa,
Y ba  a+ Y bb
a+ Y bb  b+ Y bc
b+ Y bc  c=
c=  bb,
bb,
где собственные проводимости узлов a и b:
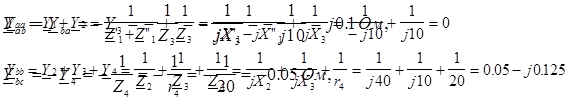
взаимные проводимости узлов:
Y ac=0 (так как узлы a и c не соединены непосредственно).
В выражение собственной проводимости Y aa должна войти и проводимость ветви с источником тока. Однако, так как внутреннее сопротивление идеального источника тока равно бесконечности, проводимость этой ветви (величина, обратная общему сопротивлению ветви ZJ+r6=¥+30=¥) равна нулю.
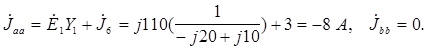
Узловые токи определяются так:
Подставив в исходные уравнения числовые значения проводимостей и узловых токов, получим систему уравнений
 0×
0×  a+(j0.1)
a+(j0.1)  b+0×
b+0×  c=-8;
c=-8;
(j0.1)  a+(0.05-j0.125)
a+(0.05-j0.125)  b–0.05×j80=0.
b–0.05×j80=0.
Решив эти уравнения, найдем потенциалы узлов a и b:
 a=j100 B,
a=j100 B,  b=j80 B.
b=j80 B.
Выберем направления напряжений во всех ветвях схемы (напряжения между узлами) и определим их. Например:
 ab=
ab=  a–
a–  b=j100–j80=j20,
b=j100–j80=j20,
 bc=
bc=  b–
b–  c=j80–j80=0,
c=j80–j80=0,
 ad=
ad=  a–
a–  d=
d=  a–0=j100,
a–0=j100,
 bd=
bd=  b–
b–  d=j80,
d=j80,
 ac=
ac=  a–
a–  c=j100–j80=j20,
c=j100–j80=j20,
 ac=
ac=  ab+
ab+  bc=j20+0=j20.
bc=j20+0=j20.
Наконец, определим токи в ветвях, направление которых указано на схеме (см. рис. 13):
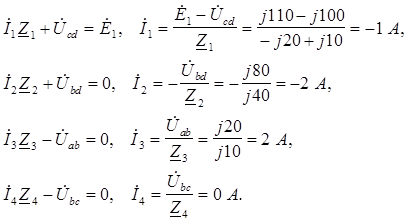 |
Ток  5 в ветви с идеальной ЭДС
5 в ветви с идеальной ЭДС 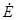 5 найдем из уравнения, составленного по первому закону Кирхгофа для узла d
5 найдем из уравнения, составленного по первому закону Кирхгофа для узла d
-  1–
1–  2–
2–  5=0, откуда
5=0, откуда  5=-
5=-  1–
1–  2=-(-1)-(-2)=3 А.
2=-(-1)-(-2)=3 А.
Для узла c
 4+
4+  5+
5+ 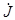 6=0, откуда
6=0, откуда  5=-
5=-  4+
4+ 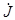 6=0+3=3 А.
6=0+3=3 А.
Проверка. Составляем уравнения по первому закону Кирхгофа:
для узла a 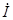 1+
1+ 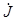 6–
6– 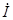 3=0, -1+3-2=0,
3=0, -1+3-2=0,
для узла b 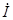 3+
3+ 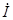 2–
2– 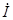 4=0, 2-2+0=0.
4=0, 2-2+0=0.
Показания вольтметра: V=| 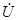 ac|=20 B.
ac|=20 B.
Пример 6. В схеме (рис. 14) заданы: E1=E2=E3=100 B, E1 и E2 по фазе опережают E3 на 90°, r1=XL2=20 Ом, XС3=10 Ом. Определить ток I3.
Рассмотрим на данном примере три метода расчета:
1) с предварительным эквивалентным преобразованием активных параллельных ветвей;
2) методом двух узлов;
3) методом эквивалентного генератора.

Записываем комплексные действующие значения ЭДС, принимая начальную фазу ЭДС E3 равной нулю: 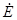 3=E3ej0°=E3=100.
3=E3ej0°=E3=100.
Тогда 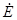 1=E1ej90°=jE1=j100,
1=E1ej90°=jE1=j100, 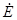 2=j100.
2=j100.
Комплексные сопротивления ветвей Z 1=r1=20, Z 2=jXL2=j20,
Z 3=-jXC3=-j10.
Решение. Заменяем параллельные активные ветви с ЭДС E1 и E2 одной эквивалентной, выбрав направление EЭ (рис. 15).

Тогда
Значение тока 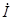 3 в схеме (см. рис. 15) находим из уравнения, составленного по второму закону Кирхгофа
3 в схеме (см. рис. 15) находим из уравнения, составленного по второму закону Кирхгофа 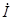 3(Z 3+ Z Э)=
3(Z 3+ Z Э)= 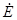 3+
3+ 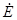 Э,
Э,
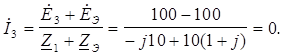
откуда
Задаваясь положительным направлением напряжения между узлами схемы (см. рис. 14), например, 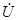 ab, определим его по формуле метода двух узлов:
ab, определим его по формуле метода двух узлов:

При этом значении узлового напряжения находим ток 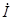 3 из уравнения, составленного по второму закону Кирхгофа для контура, состоящего из ветви с
3 из уравнения, составленного по второму закону Кирхгофа для контура, состоящего из ветви с  3 и найденного напряжения
3 и найденного напряжения 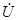 ab:
ab:
 |
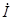 3 Z 3–
3 Z 3– 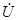 ab=
ab= 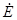 3, откуда
3, откуда
Согласно методу эквивалентного генератора размыкаем ветвь с искомым током 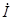 3 и исключаем из нее пассивный элемент Z 3. В полученной схеме (рис. 16) имеем левый контур, в котором протекает ток
3 и исключаем из нее пассивный элемент Z 3. В полученной схеме (рис. 16) имеем левый контур, в котором протекает ток 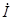 ', определяемый из уравнения
', определяемый из уравнения 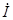 '(Z 1+ Z 2)=
'(Z 1+ Z 2)=  1+
1+ 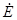 2,
2,
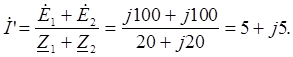
Далее, выбрав любой контур, например правый, в который входит неизвестное напряжение 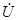 mn на зажимах разомкнутой ветви, составляем уравнение по второму закону Кирхгофа при указанном направлении обхода: -
mn на зажимах разомкнутой ветви, составляем уравнение по второму закону Кирхгофа при указанном направлении обхода: - 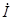 ' Z 2+
' Z 2+ 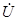 mn=-
mn=-  2+
2+  3.
3.
Напряжение
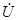 mn=-
mn=- 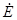 2+
2+ 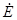 3–
3– 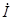 ' Z 2=-j100+100+(5+j5)j20=0.
' Z 2=-j100+100+(5+j5)j20=0.
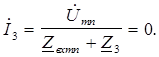
Следовательно, ток
Библиографический список.
1. Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. – М.: Высш. шк., 1997. – 559 с.
2. Новгородцев А. Б. 30 лекций по теории электрических цепей. – СП.: Политехника, 1995. – 519 с.
3. Атабеков Г. И. Теоретические основы электротехники. – М.: Энергия, 1980. – 480 с.
4. Сборник задач по теоретическим основам электротехники /Под ред. Л. А. Бессонова/. – М.: Высш. шк., 1988. – 504 с.
5. Шебес М. Р., Каблукова М. В. Задачник по теории электрических цепей. – М.: Высш. шк., 1990. – 544 с.
Содержание
стр.
Общие требования и методические указания................................... 3
Задача №1. Методы расчета резистивных цепей............................. 3
Задача №2. Анализ цепей синусоидального тока.......................... 14
Библиографический список............................................................. 27
Объем 1.75 печ. л. Тираж 100 экз.
 2020-10-12
2020-10-12 114
114






