План:
1. Сущность инфляции.
2. Учет инфляции.
Инфляция и начисление по простым процентам.
Инфляция и начисление по сложным процентам.
Измерение реальной ставки процента.
Литература:
1. Е.М. Четыркин. Финансовая математика. (стр. 83).
2. М.С. Красс, Б.П. Чупрынов. Математика в экономике. Математические методы и модели. М. Финансы и статистика. 2007 г. стр.211 – 214.
«…И запомни, Золушка, ровно в полночь
твои пятьдесят тысяч превратятся в
жалкие пятьдесят рублей.»
Рыночная фея из Интернета
1. Сущность инфляции.
Под инфляцией понимается обесценивание денег, когда на ту же самую сумму некоторое время спустя можно купить меньше товара. Инфляция возникает при нарушении баланса между товарным и денежным потоками. Внешним признаком инфляции служит непрерывный рост общего уровня цен, охватывающий все рынки и все товары, в течение достаточно длительного промежутка времени.
Для обеспечения баланса товаров и денег общая сумма денег в стране с учетом их оборачиваемости за год должна быть такова, чтобы можно было выкупить произведенные за год инвестиционные и потребительские товары (стоимость расходуемых материалов входит в стоимость упомянутых товаров), т.е. валовой общественный продукт (ВВП). Именно это положение реализуется в основном макроэкономическом уравнении:
Mv = PY, (1)
где M – общая масса денег, находящихся в обращении;
v – скорость оборота денег за год;
P – общий уровень цен (например, индекс цен по отношению к ценам базового года);
Y – натуральное значение ВВП (например, ВВП в неизмененных ценах базового года).
Необходимо учитывать выпуск облигаций, состояние рынка ценных бумаг, внешнюю торговлю. Соотношение (1) обычно записывается в форме M = kPY, где k – коэффициент, зависящий от скорости оборота денег (обратно пропорционально) и от других перечисленных факторов.
Для включения инфляционных процессов достаточно, чтобы совокупный спрос превосходил совокупное предложение. По источникам этого превышения инфляции делятся на инфляцию спроса и инфляцию предложения.
Инфляция спроса возникает тогда, когда темпы роста совокупного спроса превышают темпы роста ВВП. Увеличение совокупного спроса может произойти за счет роста ряда показателей, главными из которых являются фонд потребления, инвестиции, государственные расходы, чистый экспорт. Из уравнения (1) видно, что при увеличении левой части (как за счет роста скорости оборота денег, так и за счет увеличения денежной массы) правая часть при фиксированном объеме выпуска товаров Y может возрасти лишь за счет роста цен.
Инфляция предложения вызывается ростом издержек производства и как следствие сокращением совокупного предложения. Два самых важных источника роста издержек: повышение номинальной заработной платы и увеличение цен на сырье и энергоносители. Если денежная масса или объем выпуска товаров остались неизменными, то единственным средством для обеспечения равенства (1) служит рост цен.
В реальной экономике эти два типа инфляции разделить нельзя, они присутствуют одновременно. Инфляция спроса существует до тех пор, пока существуют чрезмерные общие расходы.
2. Учет инфляции.
В рассматриваемых ранее методах наращения все денежные величины измерялись по номиналу. То есть, не принималось во внимание снижение реальной покупательной способности денег за период, охватываемый операцией. Однако в современных условиях инфляция в денежных отношениях играет заметную роль, и без ее учета конечные результаты часто представляют собой условную величину.
Определение: инфляция – процесс общего роста цен, приводящего к снижению покупательной способности номинальной денежной единицы.
Инфляцию необходимо учитывать по крайней мере в двух случаях:
1) при расчете наращенной суммы денег;
2) при измерении реальной эффективности (доходности) финансовой операции.
Остановимся на этих проблемах.
Введем обозначения:
S – наращенная сумма денег, измеренная по номиналу,
C – наращенная сумма с учетом ее обесценивания,
Jp – индекс цен, (отношение цены на продукт в момент времени t к цене в момент s - за период с s до t); 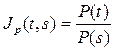 . P(t) – новые цены в условиях инфляции; P(s) – старые цены. Индекс цены (индекс инфляции) – величина безразмерная, выражаемая в долях или в процентах. Индекс цен показывает, во сколько раз выросли цены за указанный промежуток времени.
. P(t) – новые цены в условиях инфляции; P(s) – старые цены. Индекс цены (индекс инфляции) – величина безразмерная, выражаемая в долях или в процентах. Индекс цен показывает, во сколько раз выросли цены за указанный промежуток времени.
Jc - индекс, характеризующий изменение покупательной способности денег за период.
Очевидно, что C = S ´ Jc.
Индекс покупательной способности денег (Jc), равен обратной величине индекса цен – чем выше цены, тем ниже покупательная способность:
Jc = 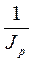 .
.
Указанные индексы, естественно, должны относиться к одинаковым интервалам времени.
Пример: Пусть сегодня получено 150 тыс. руб. Известно, что за два предшествующих года цены увеличились в 1,5 раза (или повышение на 50%), индекс цен (Jp) равен 1,5, индекс покупательной способности денег (Jc) равен 1\1,5. Следовательно, реальная покупательная способность 150 тыс. руб. составит
C = S ´ 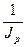 = 150 ´
= 150 ´ 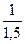 = 100 тыс. руб. в деньгах с покупательной способностью двухлетней давности.
= 100 тыс. руб. в деньгах с покупательной способностью двухлетней давности.
Для количественной характеристики инфляции используется также относительный прирост цен – темп инфляции за исследуемый период (измеряется в процентах).
Под темпом инфляции h понимается относительный прирост цен за период.
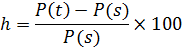
Нетрудно связать индекс цен (Jp) и темп инфляции h.
Годовой индекс цен составит Jp= 1 + h, тогда темп инфляции равен h = (Jp – 1),
обычно он измеряется в процентах и определяется как
h = 100(Jp – 1).
В свою очередь
Jp = 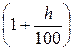 ;
;
Например: если темп инфляции за период равен 30%, то это означает, что цены выросли в 1,3 раза.
Если h – постоянный (неизменный) ожидаемый (или прогнозируемый) темп инфляции за один период, то за n таких периодов получим:
Jp = 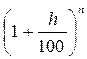 или
или 
Грубейшей ошибкой, которая, к сожалению, встречается в российской практике, является суммирование (!) темпов инфляции отдельных периодов для получения обобщающего показателя за весь срок, что существенно занижает величину получаемого показателя.
Пример: Постоянный темп инфляции 5% в месяц. Определить рост цен за год.
Jp = 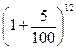 = 1,796
= 1,796
Таким образом, действительный годовой темп инфляции равен
h = 100 (Jp –1) = 100(1,796 –1) = 79,6%
а не 60% как при суммировании (5% ´ 12 = 60%).
Инфляция является цепным процессом. Следовательно, индекс цен за несколько периодов равен произведению цепных индексов цен:
Jp = 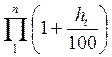 ,
,
где ht – темп инфляции в период t и при неизменном темпе прироста цен h (ht = cons = h) имеем:
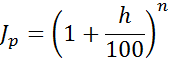
Постоянное значение темпа инфляции (за отдельный период) определяется через индекс цен по формуле
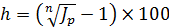
Инфляция и начисление по простым процентам.
Если наращение производится по простой ставке, то наращенная сумма с учетом покупательной способности равна:
C = 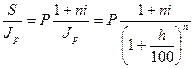 . (2)
. (2)
где 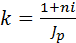 - коэффициент наращения с учетом инфляции.
- коэффициент наращения с учетом инфляции.
Как видим, увеличение наращенной суммы с учетом ее инфляционного обеспечения имеет место только тогда, когда 1 + ni > Jp.
Определим критическое значение годовой процентной ставки 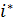 , при котором в условиях инфляции эффективность от операции наращения равна нулю. Эффективность от операции будем измерять годовой процентной ставкой.
, при котором в условиях инфляции эффективность от операции наращения равна нулю. Эффективность от операции будем измерять годовой процентной ставкой.
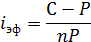
iэф = 0 при С = Р, т.е. 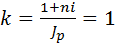
Следовательно, годовая процентная ставка, которая при начислении простых процентов компенсирует инфляцию определяется через индекс цен и равна
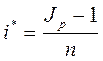
Владельцы денег не могут смирится с их инфляционным обесцениванием и предпринимают различные попытки компенсации потерь.
Применяется способ компенсации потерь от снижения покупательной способности денег при начислении простых процентов.
Наиболее распространенной является корректировка ставки процента, по которой производится наращение, т.е. увеличение ставки на величину так называемой инфляционной премии.
Скорректированная таким образом ставка называется брутто – ставкой. Брутто – ставка, которую обозначим r, находится из равенства скорректированного на инфляцию множителя наращения по брутто – ставке множителю наращения по реальной ставке процента:
При наращении по простым процентам имеем
1 + nr = (1 + ni) Jp,
где Jp – индекс цен за учитываемый период
отсюда находим:
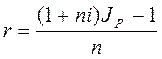
Наращение по ставке r не только компенсирует инфляцию, но и обеспечивает номинальную доходность i.
Инфляция и начисление по сложным процентам.
Наращенная по сложным процентам сумма к концу срока с учетом инфляционного обеспечения находится так:
C = 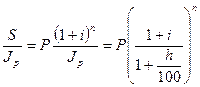 (3)
(3)
Величина, на которую умножается P в формуле (3), представляет собой множитель наращения, учитывающий ожидаемый уровень инфляции.
Критическое значение годовой процентной ставки i*, при которой в условиях инфляции эффективность от операции наращения равна нулю, определяется при 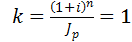
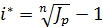
или через темп инфляции
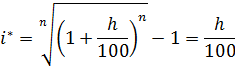
Т.е. годовая процентная ставка сложных процентов, обеспечивающая нулевую эффективность операции в условиях инфляции, совпадает с темпом инфляции, выраженным в долях единицы.
Применяют два способа компенсации потерь от снижения покупательной способности денег приначислении сложных процентов.
1) Корректировка ставки процента, по которой производится наращение, т.е. увеличение ставки на величину так называемой инфляционной премии.
Определим брутто-ставку r при условии полной компенсации инфляции. При наращении по сложной процентной ставке находим брутто-ставку из равенства
r +1=( 1 +i)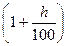 .
.
или 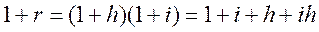
где i – реальная ставка.
Откуда
r = i +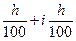 или
или 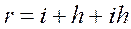 - формула Фишера. (4)
- формула Фишера. (4)
Эта формула связывает номинальную процентную ставку i с реальной i* и темпом инфляции h.
На практике ставку рассчитывают проще:
r = i + 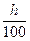 (5)
(5)
Инфляционная премия равна 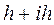 .
.
Посмотрим теперь, как совместно влияют сложная ставка i и темп инфляции h на значение этого множителя 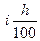 (или
(или 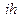 ).
).
- Очевидно, что если среднегодовой темп инфляции равен процентной ставке, то роста реальной суммы не произойдет – наращение будет поглощаться инфляцией, и следовательно, C = P.
- Если же h/100 > i, то наблюдается «эрозия» капитала – его реальная сумма будет меньше первоначальной.
- Только в ситуации, когда h/ 100 < i, происходит реальный рост, реальное накопление.
|
| ||||
 | |||||
i = h

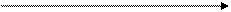
i < h
n
Формула (4) по сравнению с (5) содержит один дополнительный член, которым при незначительных величинах i и h можно пренебречь. Если же они значительны, то ошибка (не в пользу владельца денег) станет весьма ощутимой. Например, даже при i = 5% и h = 1% «вклад» этого произведения в брутто-ставку составит 0,0005, или 0,05%. Брутто-ставка в этом случае равна 6,05% (вместо 15% по формуле (4)). Однако при годовой инфляции в 100% и той же исходной ставке наращения брутто-ставка увеличивается уже до 0,05 + 1 + 0,05´1 = 1,1 т.е. до 110%.
Пример: Предполагается, что темп инфляции составит 20% в год. Какую ставку сложных процентов следует проставить в договоре, чтобы реальная доходность составляла 10%? Чему равна инфляционная премия?
Решение. Брутто – ставку вычислим по формуле (4)
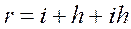 = 0,1 + 0,2 + 0,1*0,2 = 0,32
= 0,1 + 0,2 + 0,1*0,2 = 0,32
Инфляционная премия составит:
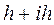 = 0,2 + 0,1*0,2 = 0,22
= 0,2 + 0,1*0,2 = 0,22
В договоре следует проставить ставку сложных процентов, равную 32% годовых, при этом инфляционная премия будет равна 22%
2) Индексация (корректировка) первоначальной суммы Р.
В этом случае сумма Р корректируется согласно движению заранее оговоренного индекса. Тогда получаем:
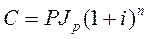
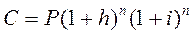
Очевидно, что при больших темпах инфляции корректировка (индексация) ставки имеет смысл только для кратко – или в крайнем случае среднесрочных операций.
Пример: Кредит в размере 500 тыс. руб. выдан на 2 года. Реальная доходность операции должна составлять 20% годовых по сложной ставке процентов. Ожидаемый уровень инфляции составляет 15% в год. Определить множитель наращения, учитывающий инфляцию и наращенную сумму.
Решение. Множитель наращения определяется по формуле
 =
= 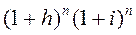 = (1 +0,15)2 (1 + 0,2)2 = 1,9
= (1 +0,15)2 (1 + 0,2)2 = 1,9
Наращенная сумма: 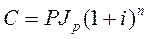 = 500 * 1,9 = 950 (тыс.руб.)
= 500 * 1,9 = 950 (тыс.руб.)
Множитель наращения, учитывающий инфляцию, составляет 1,9. Наращенная сумма – 950 тыс. руб.
Измерение реальной годовой ставки процента (i).
На практике приходится решать и обратную задачу – находить реальную годовую ставку процента в условиях инфляции.
Аналогичный по содержанию показатель, но при начислении простых процентов, находим как
i = 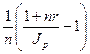 или
или 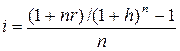
Как видим, реальная доходность здесь зависит от срока операции. Положительной простая ставка i может быть только при условии, что 1+ nr > Jp Компенсации инфляции можно достичь и путем индексации исходной суммы задолженности.
Если r объявленная норма доходности (или брутто-ставка), то реальный показатель доходности в виде годовой процентной ставки i можно определить при наращении сложных процентов на основе формулы (3)
i = 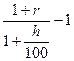 или
или 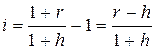
Пример: На годовой вклад помещены денежные средства по ставке 12% годовых. Инфляция составляет 10% в год. Найти реальную ставку процентов для случая простых и сложных процентов при n = 2.
Решение. При начислении простых процентов годовая реальная ставка определяется по выражению:

При начислении сложных процентов реальная ставка процентов определяется по формуле:
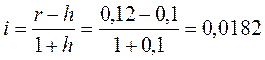
Реальная ставка простых процентов составляет 1,24%, сложных 1,82%.
 2014-02-04
2014-02-04 28391
28391