Тема 1. Понятие о культуре делового общения

Классификация кривых второго порядка.

ЛИТЕРАТУРА

ОБУЧЕНИЕ ГРАММАТИКЕ, ПРАВОПИСАНИЮ И РАЗВИТИЮ РЕЧИ. НАУЧНЫЕ ОСНОВЫ ОБУЧЕНИЯ ГРАММАТИКЕ

Цели:

показать взаимосвязь методики обучения грамматике с другими науками;

раскрыть сущность преподавания грамматики в начальной школе.

План:

1) взаимосвязь методики обучения грамматике с философией;

2) основополагающие данные языкознания;

3) необходимость знаний психологии и педагогики;

4) невозможность обучения без знаний передового опыта.

1) Айдарова Л.И. Психологические проблемы обучения младших школьников русскому языку. – М., 1978.

2) Выготский Л.С. Избранные психологические исследования. – М., 1956.

3) Золотова Г.А. О возможностях перестройки в преподавании русского языка. Русский язык в школе. – 1989. - №5.

4) Львов М.Р., Рамзаева Т.Г., Светловская Н.Н. Методика обучения русскому языку в начальных классах. – М., 1987.

5) Русский язык в начальных классах. Под редакцией Соловейчика М.С. – М., 1993.

Одна из важнейших задач обучения и воспитания школьников -формирование у них системы научных взглядов на мир, поэтому методика русского языка опирается на такую науку, как философия.

Каждая учебная дисциплина вносит определенный вклад в форми­рование у учащихся элементов научного мировоззрения. В начальной школе это в большей мере осуществляется на уроках чтения и природоведения, но и уроки русского языка через грамматический материал выполняют эту задачу (разделы "Лексика", "Фонетика", "Словообразование" особенное место занимают).

Сущность языка как общественного явления выражается в его коммуникативной функции. Ведущее направление в изучении русского язы­ка в школе, в том числе и начальной, - осознание учащимися коммуникативной функции языка.

Методика обучения грамматике опирается на научные данные языкознания. Грамматика сама является разделом языкознания, которая изучает строй слова и предложения в языке. В начальной школе мы имеем дело с элементарными сведениями по языкознанию, но они даются научно. Например, различение букв и звуков вол - вёл, угол - уголь и т.д.

Методика обучения грамматике опирается на данные психологии.

Грамматические понятия носят отвлеченный характер предмета, признака, действия - абстракция, которую ребенок может усвоить лишь постепенно.

Рука, ручка, парта - предметы, но и мысль, доброта, зло - с точки зрения грамматики тоже предметы.

Дети привыкли видеть в словах реальные значения, а грамматика говорит не о лексических, а о формальных, грамматических значениях слов.

Возникавшее у детей противоречие между реальными и формальными признаками слова надо примирить. Опираясь на данные психологии, методика разрабатывает систему упражнений, которые помогают решить данное противоречие. Мы учим детей приемам умственной деятельности, которые помо­гают обобщить знания и выработать навыки отличия одной орфограммы от другой.

Методика, опирается на научные данные педагогики.

- учебный материал должен быть доступен детям;

- использовать наглядные пособия, так как мышление в этом возрасте конкретное;

- учитывать принцип преемственности и перспективности (в каждом клас­се дети получают знания, которые становятся фундаментом для полученных сведений в следующих классах);

- отбирать дидактический материал, ценный в воспитательном значении, а методические приемы должны способствоватъ развитию детей;

- новые знания, умения и навыки приобретается сознательно, а это лучше всего происходит, если дети самостоятельно добывают эти знания, дела­ют выводы и обобщения, выводят правила.

Методика обучения грамматике опирается на передовой опыт школы, города, района и т.д.

От грамматики следует отличать правописание (графику, орфографию, пунктуацию). Правописание опирается на грамматику, но имеет свои особенности.

Важной задачей аналитической геометрии является исследование общего уравнения линии второго порядка и приведение его к простейшим (каноническим) формам.

Пусть дано общее уравнение линии второго порядка:

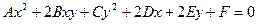. (1)

Задача состоит в том, чтобы перейти, от так сказать, «случайной» системы координат к «естественной» для данной кривой.

Уточним предъявляемые требования:

1. нужно добиться, чтобы в группе старших членов исчез член с произведением текущих координат;

2. чтобы число членов первой степени стало меньшим (если возможно, - совсем их уничтожить);

3. кроме того, если возможно, уничтожить свободный член.

Уравнение, получаемое при соблюдении этих требований, называется каноническим.

Покажем на примерах, как следует выполнять необходимые действия, чтобы привести данное уравнение к каноническому виду.

Рассмотрим теперь пример полного преобразования уравнения линии 2 – го порядка с помощью параллельного переноса и поворота системы координат.

Привести к каноническому виду уравнение линии. Выполнить построение линии:

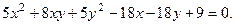
Прежде всего постараемся упростить выражение при помощи параллельного переноса координатных осей. Перенесём начало координат в точку 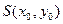, которую пока будем считать произвольной. Получим соответствующее преобразование координат по формулам (2): 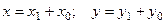. Получим:

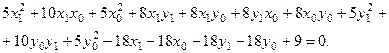
С помощью параллельного переноса мы должны избавиться от линейных слагаемых в уравнении, т.е. приравниваем нулю:

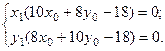
Эти равенства должны выполняться для всех 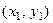, т.е. получаем систему:

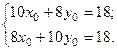Тогда: 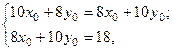или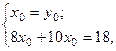

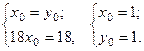
Таким образом, перенос системы координат необходимо произвести в точку 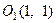. При этом получим уравнение:

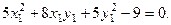
Чтобы избавиться от смешанного произведения 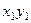, выполним поворот системы координат по формулам (4):

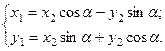
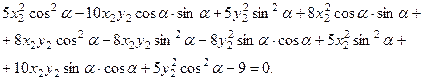
Нам необходимо убрать смешанное произведение, поэтому группируем соответствующие коэффициенты и приравниваем их к нулю:

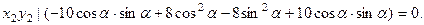Учитывая тригонометрические формулы, получаем:

.

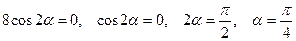Перепишем уравнение линии, с учётом того, что смешанного произведения в уравнении не осталось:

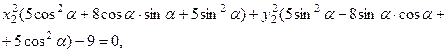или, 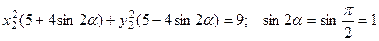и тогда: 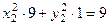и, окончательно,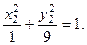

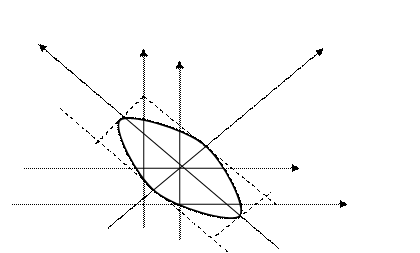
Получили каноническое уравнение эллипса с полуосями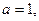

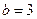. Построим данную линию: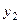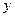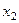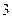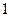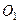

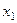
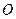1

1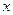

Рассмотрим ещё примеры: Пример 1. Построить следующую линию: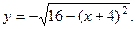

Из уравнения видим, что должно быть выполнено: 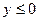. Возведём равенство в квадрат: 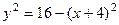. Тогда 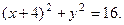Получено уравнение окружности с центром в точке 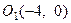радиуса 4.

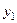
С учётом условия 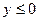, мы получаем нижнюю часть окружности.

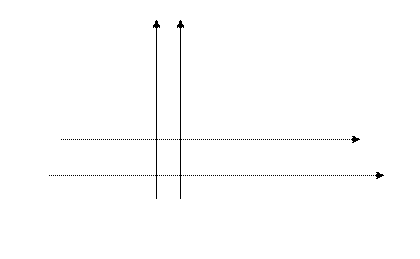
Пример 2. Построить линию: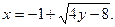

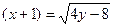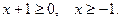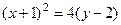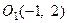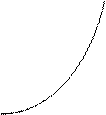
. Ограничение: Возведём последнее равенство в квадрат . Это уравнение параболы с вершиной в точке . . 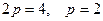Построим линию:

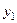
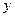
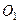2

-1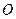

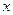
Ввиду условия 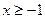, выбираем правую ветку параболы.

Лекция №

§ 7 ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ.

Полярная система координат на плоскости определяется заданием некоторой точки 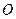, называемой полюсом; исходящего из этой точки луча 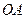, называемого полярной осью и масштабной единицей 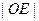для измерения длин.

Для произвольной точки 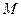плоскости координатами в данной системе координат называют полярный радиус 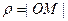, вычисленный в масштабных единицах, и полярный угол 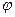между осью 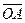и радиус – вектором 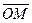, т.е. ,

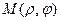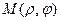
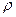
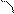
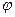
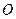1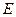

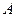
Чаще всего предполагают, что 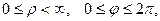или 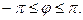Иногда допускаются отрицательные значения для 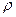, но при этом соответствующие значения откладываются на продолжении луча.

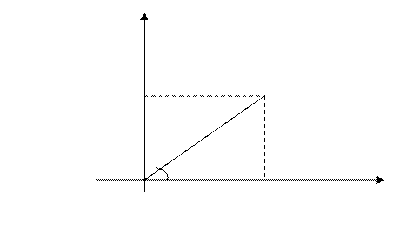Установим связь между полярными координатами точки и её декартовыми координатами. Для этого совместим начало декартовой системы координат с полюсом полярной системы координат, а ось 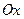- с полярной осью:

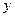
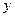
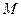
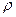
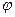
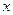
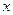
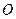
Используя тригонометрические формулы легко получаются формулы перехода от декартовых координат к полярным:

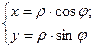(1)

и формулы обратного перехода от полярных координат к декартовым:

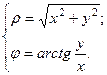(2)

Чаще всего эти формулы используются комбинированно.

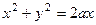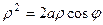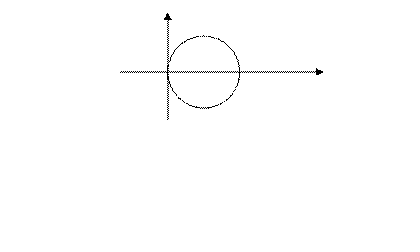
Окружность в полярной системе координат имеет уравнение , или 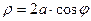, тогда данная линия имеет вид:

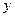
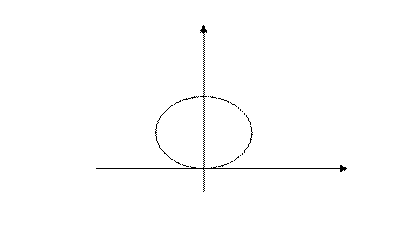Аналогичным образом, окружность 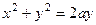имеет в полярных координатах уравнение, 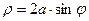и соответствующий рисунок линии выглядит следующим образом:

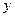
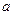
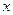
Окружность 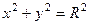с центром в начале координат в полярных координатах имеет уравнение 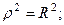или .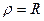

Если задано уравнение линии в полярных координатах 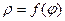, то чтобы построить данную линию в полярной системе координат, заполняют таблицу значений этой функции в точках, вычисленных для значений аргумента 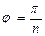, причём, чем больше 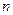, тем точнее будет построение линии.

Пример 1. Построить линию: .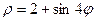

Заполнить таблицу значений данной функции:

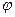
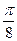
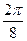
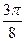
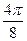
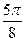
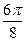
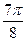
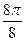
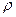
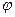
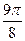
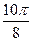
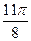
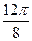
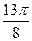
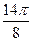
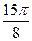
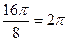
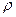
Построим данную линию

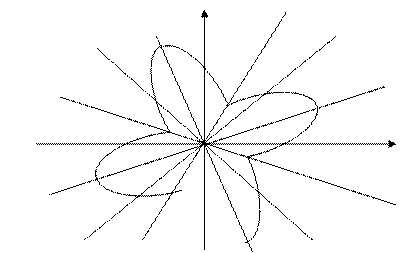
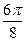
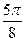
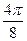
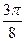
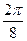
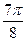
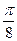
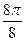
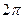
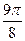
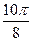
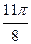
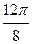
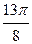
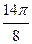
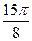
При построении линии в полярных координатах можно поступать и иначе, а именно, используя свойства соответствующих функций.

Пример 2. Пусть дано уравнение 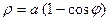. Так как 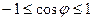, то максимальное значение данная функция принимает при 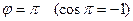- 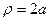; минимальное значение будет в точке - .

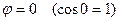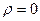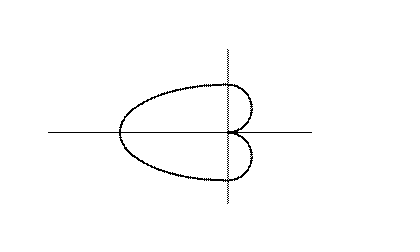Так как 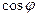чётная функция, то 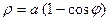также чётная функция и поэтому соответствующая линия симметрична относительно полярной оси. Таким образом, получаем линию:

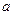
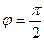
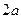
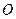
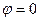
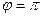
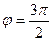
Эту линию называют кардиоидой, имея ввиду её форму.

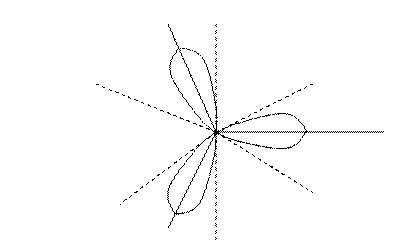
Пример 3. Построить линию .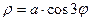

Достаточно построить данную линию на промежутке 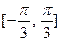, так как период данной функции равен 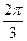. Учитывая, что 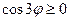в промежутке 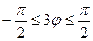, следовательно 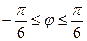. После этого, учитывая периодичность функции, можно построить ещё две части этой линии, которые получаются при .

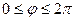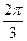
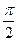
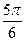
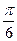
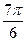
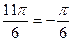
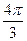
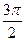
В заключение параграфа напишем уравнение эллипса, гиперболы и параболы в полярных координатах.

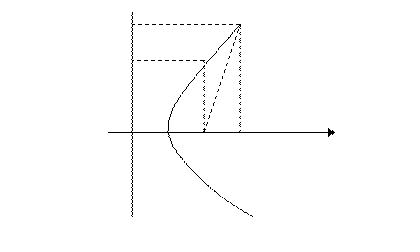Пусть 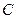- дуга эллипса, гиперболы или параболы:

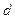
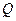
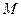
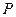
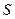
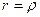
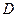
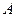
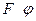
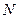
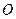
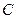
Совместим фокус 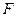с полюсом, а ось симметрии - с полярной осью. Точка 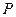выбрана так, что 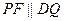. По свойству директрисы: 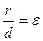. Пусть 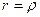, 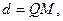или 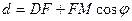. Для точки 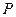имеем 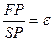. Тогда, 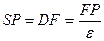. Обозначив 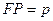, получим 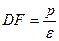. Следовательно, 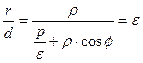, отсюда: 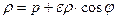, или 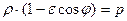. Окончательно получаем уравнение:

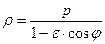. (3)

При 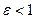- это уравнение эллипса; при 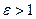- это уравнение одной ветки гиперболы; при 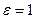- это уравнение параболы.

Пример 4. Построить линию 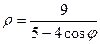и записать её уравнение в декартовой системе координат.

Можно произвести построение данной линии непосредственно в полярной системе координат, как в примере 1. Но в данном случае, учитывая формулу (3), это уравнение эллипса с 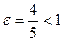. Поэтому более удобно сначала перейти к декартовым координатам и только после этого построить линию (менее трудоёмкий вариант решения). Преобразуем уравнение линии: 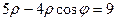. Используя формулы (1) и (2), получаем:

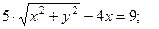
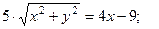(4) обе части полученного равенства возведём в квадрат:

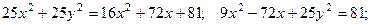
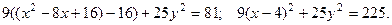
Получено каноническое уравнение эллипса:

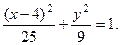
Его центр симметрии 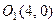, полуоси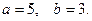

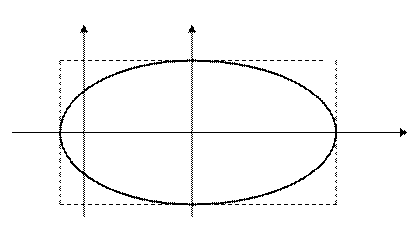Построим данную линию:

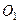4 5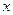

Уравнение вида 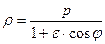также определяет линию 2 – го порядка, но в этом случае сдвиг точки 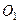происходит влево, а уравнение 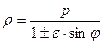приводит к смещению линии по оси .

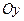Общением называют «…процесс установления и развития контактов между людьми, обусловленный потребностями в совместной деятельности и включающий в себя обмен информацией, выработку единой стратегии взаимодействия, восприятие и понимание другого человека».

Важнейшая особенность делового общения в том, что нужно уметь строить отношения с разными людьми, добиваясь максимальной эффективности деловых контактов. А также, мы должны отчётливо представлять, что партнёра по общению интересует прежде всего то, насколько мы ему полезны.

Под культурой общения следует понимать высокий уровень умения общаться в деловом мире. Это предполагает:

1. Высокую коммуникативную культуру, т.е. искусство говорить и слушать.
2. Умение объективно воспринимать и правильно понимать партнёра.
3. Умение строить отношения с любым партнёром, добиваться эффективного взаимодействия на основе обоюдных интересов.

Подлинная культура делового общения предполагает и высокую этическую культуру, умение видеть в деловом партнёре не только нужную, но и интересную личность.

«Требование честности в бизнесе вытекает из его природы. Обман не может служить основой для нормального экономического процесса. Сейчас без честности и порядочности в отношениях между промышленными предприятиями, банками, отдельными людьми цивилизованное предпринимательство просто невозможно. Миллионы тон нефти, десятки миллионов акций и других ценных бумаг ежедневно продаются и покупаются на основе устных сделок без свидетелей. Честность и порядочность были присущи и русскому купечеству» (специалист по этике и психологии бизнеса профессор Ф.А. Кузин).

Формула успеха западных предпринимателей:

Преуспевание = профессионализм + порядочность

Из всех возможных способов передачи информации речь – самое универсальное средство, т.к. она позволяет точнее всего передать смысл сообщения.. Выступление на совещании, заключение договора, посредническая и рекламная деятельность – всё это требует красноречия – умения ясно и убедительно выражать свои мысли. Косноязычному бизнесмену трудно сделать карьеру.

«Красноречие есть нечто такое, что дается труднее, чем это кажется, и рождается из очень многих знаний и стараний» (римский оратор Цицерон).

Знание теории красноречия, изучение психологии людей, постоянная практика выступлений и упорная работа над словом – вот что даёт возможность влиять на аудиторию или партнёра.

Вопросы. Как вы оцениваете собственную культуру делового общения?

Кто из окружающих (либо всем известных) людей может служить для вас примером в деловом общении?