Фибоначчиев поиск (самостоятельно)

Примечания

1. При нечетном N необходимо ввести фиктивную запись X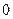с ключом K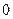< A.?

2. 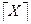- операция означает взятие от числа наименьшего целого, большего или равного Х.

Пример. Осуществить однородный бинарный поиск аргумента 30 в массиве ключей: 20 25 29 32 37 38 39 51 57 61 99.

i=6, H=6: [20 25 29 32 37 38 39 51 57 61 99].

i=3, H=3: [20 25 29 32 37]38 39 51 57 61 99.

i=5, H=1: 20 25 29[32 37]38 39 51 57 61 99.

i=4, H=0: 20 25 29[32]37 38 39 51 57 61 99.

Так как H = 0, а K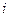# A, поиск заканчивается неудачно.

При реализации этого метода для нахождения интервала поиска

используются числа Фибоначчи. Числа Фибоначчи получаются по рекуррентной формуле

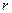F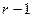= F+ F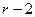, где r = 3, 4, 5,..., F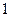= 0, F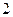= 1.

В методе Фибоначчи, так же как и в однородном бинарном поиске, используются два указателя: i - текущее положение и величина H изменения, но они выбираются в соответствии с числами Фибоначчи. Значение i выбирается равным числу Фибоначчи F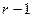, а Н - равным F.

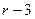Алгоритм Фибоначчиева поиска состоит из предварительного этапа и 4 шагов. Первоначально определяется такое число M>=0, что N + M + 1 = F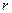, где F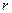> N есть ближайшее к N число Фибоначчи. Устанавливают i = F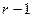, P = F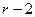, H = F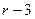. Если первый проверяемый ключ K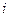< A, то устанавливают i = i - M.

Структурограмма алгоритма поиска приведена на рис.

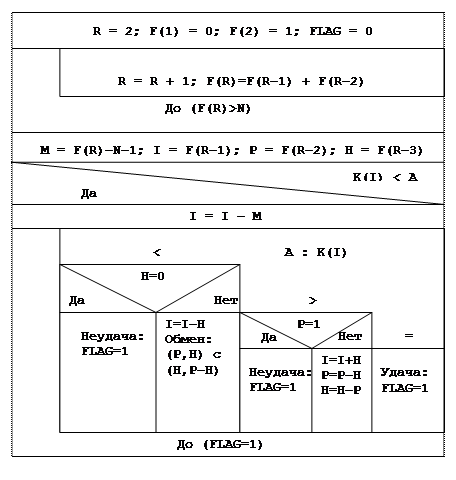
Пример 1.

1 4 5 8 9 12

А = 8, N = 6.

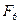= = 8; M = 1; I = 5; m = 2; P=3; 9 > 8; m # 0; I=3;

P=2; m = 1; 8 > 5; P # 1; I = 4; P=1; m=0;

1 4 5 8 9 12; Удача!

Пример 2

1 4 5 8 9 12

А = 12, N = 6.

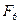= = 8; M = 1; I = 5; m = 2; P=3; 9 < 12; m # 0; I=4;

1 4 5 8 9 12;

I=6; P=1; m = 1;

1 4 5 8 9 12; Удача!

Пример 3

1 4 5 8 9 12

А = 11, N = 6.

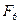= = 8; M = 1; I = 5; m = 2; P=3; 9 < 11; m # 0; I=4;

1 4 5 8 9 12

I=6;P=1; m = 1; 1 4 5 8 9 12

I = 5; P=1; m=0;

1 4 5 8 9 12; Неудача!