2014-02-02
554
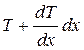
При фильтровании поток жидкости проходит через пористую перегородку. Дифференциальное уравнение движения несжимаемой вязкой жидкости для случая одномерного движения получают, выделяя в потоке жидкости, движущейся по каналу, элементарный параллелепипед объемом dV с ребрами dx, dy, dz. На этот элемент действую три силы: сила тяжести G, сила давления P, сила трения T.
Сила тяжести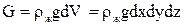 
Если на верхней грани параллелепипеда давление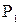 
, то проекция на верхнюю грань действует сила 
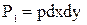. На нижней грани давление 
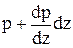, а сила давления 
.
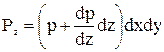Результирующая этих сил является силой давления на параллелепипед.
.
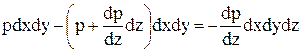Обозначим силу трения, отнесенную к ед. поверхности через Т. Сила, действующая на грань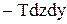 
. Сила трения у противоположной грани 
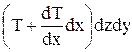. Результирующая этих сил является силой трения, действующей на параллелепипед:
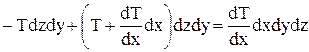
Согласно закону Ньютона: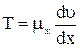 
, следовательно:
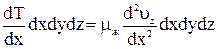
На основании закону механики равнодействующая сил равна массе умноженной на ускорение.
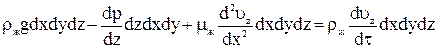
или
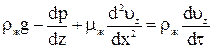
Дифференциальное уравнение носит название уравнения
НАВЬЕ-СТОКСА.
Разделим все члены уравнения на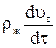 
, тогда получим:
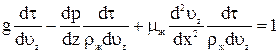
Вычеркнем из уравнения все знаки дифференцирования, а x и z заменим на линейный размер l, тогда получим:
Первое слагаемое: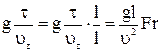 
(критерий Фруда) – характеризует отношение сил тяжести к инерционным силам.
Второе слагаемое: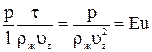 
(Критерий Эйлера) – характеризует отношение сил давления к инерционным силам.
Третье слагаемое:
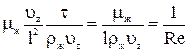- величина, обратная критерию Рейнольдса, характеризующему режим движения жидкости.
Так как при фильтровании силы тяжести малы по сравнению с силами давления и силами трения, то ими можно пренебречь, следовательно в критериальное уравнение критерий Фруда не вводится. Вместо него вводят характерный геометрический размер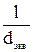 
фильтра: его толщина и диаметр перегородки:
.
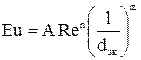Коэффициент А и показатели степеней n и m определяются экспериментально.
