Рыночная экономика
Фирмы нацелены на максимизацию прибыли. Размер прибыли зависит от действий наемных менеджеров.
Качественно отличается от двух первых. Предприятия ориентированы на выживание и на сохранение трудового коллектива. Формально не зависит от государственного бюджета.
Государство представлено правительственными учреждениями, осуществляющими юридическую и политическую власть для обеспечения контроля над хозяйственными субъектами и над рынком для достижения общественных целей.
Пусть 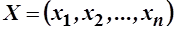 - набор товаров, заданы вектор цен
- набор товаров, заданы вектор цен 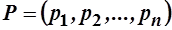 и доход потребителя
и доход потребителя 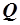 .
.
 Множество всех товаров, суммарная стоимость которых не превышает бюджет потребителя, называется бюджетным множеством:
Множество всех товаров, суммарная стоимость которых не превышает бюджет потребителя, называется бюджетным множеством: 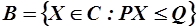 .
.
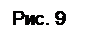 |
Утверждение 1. Бюджетное множество ограничено и замкнуто.
Множество всех товаров, суммарная стоимость которых равна доходу потребителя, называется границей бюджетного множества: 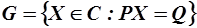 (при
(при 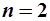 границей будет отрезок, при
границей будет отрезок, при 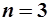 - часть гиперплоскости).
- часть гиперплоскости).
Следует отметить, что 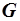 зависит от
зависит от 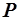 и
и 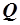 , но не зависит от системы предпочтений индивида.
, но не зависит от системы предпочтений индивида.
Сформулируем задачу потребителя: при сложившихся рыночных ценах на товары 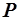 , имея определённый доход
, имея определённый доход 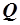 , потратить деньги с максимальной пользой. Польза понимается в смысле системы его предпочтений или его функции полезности. Это приводит к следующей задаче математического программирования:
, потратить деньги с максимальной пользой. Польза понимается в смысле системы его предпочтений или его функции полезности. Это приводит к следующей задаче математического программирования:
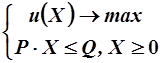 <=>
<=> 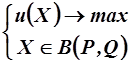 . (8)
. (8)
Поскольку 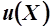 – непрерывная функция, а бюджетное множество
– непрерывная функция, а бюджетное множество 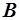 – ограничено и замкнуто, то
– ограничено и замкнуто, то 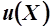 достигает на
достигает на 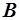 своего максимума
своего максимума 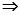 решение задачи потребителя существует.
решение задачи потребителя существует.
Утверждение 2. Любая точка максимума (обозначим её 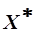 ) лежит на границе бюджетного множества
) лежит на границе бюджетного множества 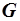 .
.
Доказательство: Допустим обратное: 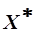 - точка максимума функции полезности
- точка максимума функции полезности 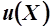 , но
, но 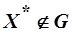 , т.е.
, т.е. 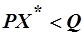 => потребитель имеет неиспользованное количество денег
=> потребитель имеет неиспользованное количество денег 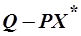 , на которые он может купить дополнительный набор товаров
, на которые он может купить дополнительный набор товаров  , причём из-за безграничной делимости товаров можно считать, что
, причём из-за безграничной делимости товаров можно считать, что 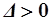 . Рассмотрим набор товаров
. Рассмотрим набор товаров 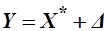 , тогда
, тогда 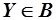 , так как денег истрачено не более
, так как денег истрачено не более 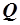 .
.
В силу свойства ненасытности: 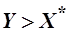 =>
=> 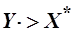 =>
=>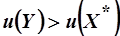 - противоречие с тем, что
- противоречие с тем, что 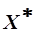 - точка максимума
- точка максимума 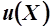 =>
=> 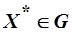 .
.
■
Утверждение 3. Если функция полезности 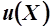 - строго выпукла, то решение задачи потребителя существует и единственно.
- строго выпукла, то решение задачи потребителя существует и единственно.
Эта единственная точка максимума называется точкой спроса или просто спросом потребителя.
Решим задачу потребителя (задачу оптимизации целевой функции 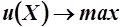 при заданном условии
при заданном условии 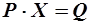 ). Составим функцию Лагранжа:
). Составим функцию Лагранжа: 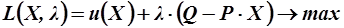 ,
,
таким образом, исходная задача сводится к задаче нахождения безусловного экстремума. Найдём частные производные и приравняем их к нулю:
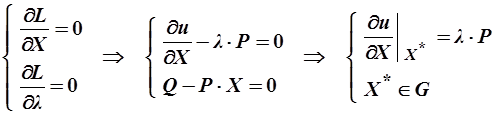 .
.
 Итак, точка спроса
Итак, точка спроса 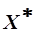 лежит на границе
лежит на границе 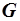 бюджетного множества и характеризуется тем, что в ней вектор предельных полезностей пропорционален вектору цен (с коэффициентом пропорциональности
бюджетного множества и характеризуется тем, что в ней вектор предельных полезностей пропорционален вектору цен (с коэффициентом пропорциональности 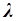 ). Можно сказать иначе: в точке спроса отношение предельной полезности товара к его цене есть величина постоянная:
). Можно сказать иначе: в точке спроса отношение предельной полезности товара к его цене есть величина постоянная: 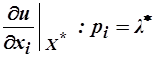 . (9)
. (9)
предельная полезность товара,
приходящаяся на одну ден. ед.
Значит, 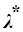 можно интерпретировать как предельную полезность добавочного дохода:
можно интерпретировать как предельную полезность добавочного дохода: 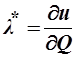 - предельная полезность денег.
- предельная полезность денег.
Если воспользоваться понятием предельной нормы замещения 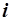 -го товара
-го товара 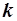 -ым, то в точке спроса:
-ым, то в точке спроса:
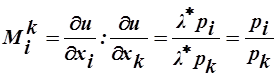 (2 -ой закон Госсена), (10)
(2 -ой закон Госсена), (10)
т.е. индивид сумеет достичь оптимальной структуры потребления, если свои личные субъективные предпочтения приведет в соответствие с объективно сложившейся ситуацией на рынке.
Пример 2.4. Пусть функция полезности имеет вид:
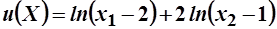 . Известны цены на товары и доход:
. Известны цены на товары и доход: 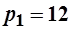 ,
, 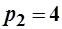 ,
, 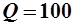 . Найдите точку спроса. Как изменится полезность, если цена на первый товар снизится до 10 ден. ед., а на
. Найдите точку спроса. Как изменится полезность, если цена на первый товар снизится до 10 ден. ед., а на
второй товар – увеличится до 5?
Решение: Сначала найдём точку спроса для первоначальных цен. Для этого воспользуемся вторым законом Госсена: 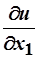 :
: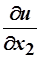 =
=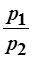 .
.
 и
и 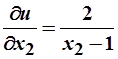 =>
=> 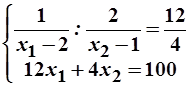 =>
=>
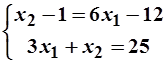 =>
=> 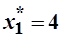 и
и 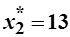 .
.
Итак, первоначальная точка спроса 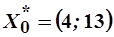 .
.
Аналогично находим новую точку спроса, соответствующую изменившимся ценам:
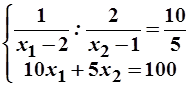 =>
=> 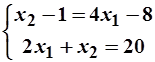 =>
=> 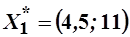 .
.
Таким образом, потребление первого товара увеличилось на 0,5 ед., а потребление второго товара уменьшилось на 2 ед.
Изменение полезности можно оценить приближенно с помощью дифференциала функции полезности:
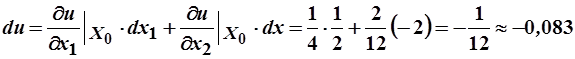 .
.
Более точно определить изменение полезности, можно вычислив приращение функции:
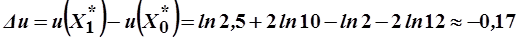 .
.
■
Функции 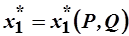 ,
, 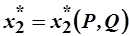 ,…,
,…, 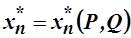 называются функциями спроса Маршалла. Если в функции полезности
называются функциями спроса Маршалла. Если в функции полезности 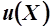 заменить
заменить 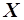 на
на 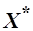 , то получим так называемую косвенную функцию полезности:
, то получим так называемую косвенную функцию полезности: 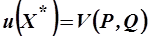 .
.
Задачу потребителя можно сформулировать иначе: выбрать из одинаково полезных наборов самый дешёвый. Математически это можно записать так:
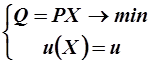 - задача на нахождение условного экстремума, которая может быть решена аналогично предыдущей с помощью множителей Лагранжа. Её решения:
- задача на нахождение условного экстремума, которая может быть решена аналогично предыдущей с помощью множителей Лагранжа. Её решения:
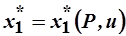 ,
, 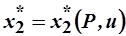 ,…,
,…, 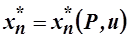 называются функциями спроса Хикса. Для них можно определить минимальный расход на оптимальный потребительский набор:
называются функциями спроса Хикса. Для них можно определить минимальный расход на оптимальный потребительский набор:
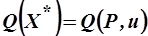 - функция расходов.
- функция расходов.
Пример 2.3. Пусть 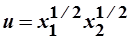 , заданы доход
, заданы доход 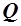 и вектор цен
и вектор цен  . Найти:
. Найти:
а) функции спроса Маршалла и косвенную функцию полезности;
б) функции спроса Хикса и функцию расходов.
Решение:
а) запишем задачу потребителя при заданных ценах на товары и доходе потребителя: 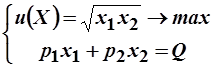 .
.
Для нахождения условного экстремума запишем функцию Лагранжа:
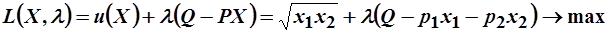
В точке экстремума должно выполняться условие:
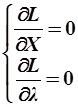 =>
=> 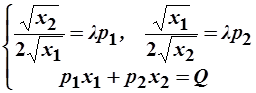 =>
=> 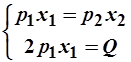 .
.
Отсюда получим функции спроса Маршалла:
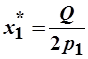 и
и 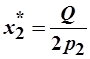 .
.
Зная спрос на товары, можно определить соответствующую функцию полезности:
 ,
,
которую называют косвенной функцией полезности.
б) В данном случае задача потребителя формулируется так: выбрать из одинаково полезных наборов самый дешёвый. Запишем это математически:
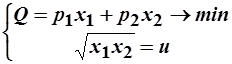 .
.
Для нахождения условного экстремума запишем функцию Лагранжа:
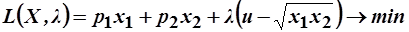 .
.
В точке экстремума должно выполняться условие:
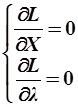 =>
=> 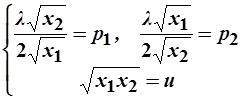 =>
=> 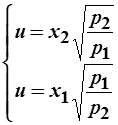 .
.
Отсюда получим функции спроса Хикса:
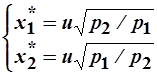 .
.
Для них определим минимальный расход на оптимальный потребительский набор:
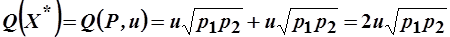 .
.
Полученная функция называется функцией расходов.
■
Пример 2.5. Функция полезности имеет вид: 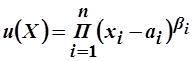 ,
,
где 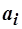 - минимально необходимое количество
- минимально необходимое количество 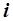 -го блага, которое
-го блага, которое
приобретается в любом случае и не является предметом выбора; 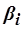 - характеристика относительной ценности блага для потребителя. Найти функции спроса Маршалла, считая заданными доход
- характеристика относительной ценности блага для потребителя. Найти функции спроса Маршалла, считая заданными доход 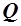 и цены
и цены 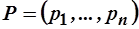 .
.
Решение: Запишем задачу потребителя при заданных ценах на товары и доходе потребителя:
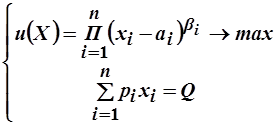
Согласно второму закону Госсена в точке максимума: 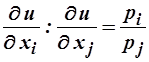 .
.
Найдём предельные полезности и приравняем их к отношению цен:
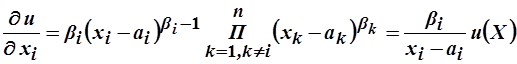 ,
,
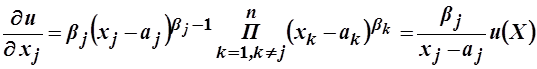 .
. 
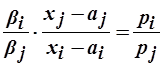
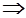
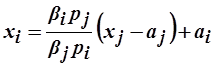 .
.
Отсюда 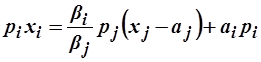 ,
,
теперь просуммируем по 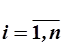 :
:
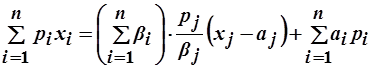
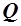
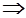 получим:
получим:
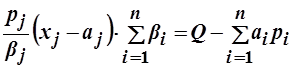
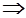
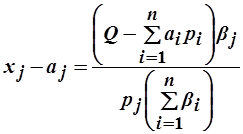 .
.
Таким образом, находим функции спроса Маршалла:
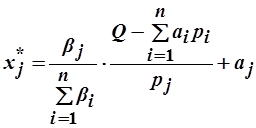 .
.
■
 2014-02-02
2014-02-02 2340
2340






