Вычисление дистанции Левенштейна. На рис. 11, 12 представлена функция levenshtein, реализующая алгоритм динамического программирования вычисления дистанции Левенштейна

На рис. 11, 12 представлена функция levenshtein, реализующая алгоритм динамического программирования вычисления дистанции Левенштейна.

Рис. 11. Прототип функции levenshtein

Рис. 12. Реализация функции levenshtein

Функция levenshtein имеет тот же набор параметров, что и функция levenshtein_r,описанная в пред. лекции. Более того, реализации этих двух функций практически одинаковы. Основное отличие – применение в функции levenshtein массива d (для работы с ним используется макрос DD) для хранения результатов промежуточных вычислений.

Интерес представляет сравнительный анализ скорости вычисления дистанции Левенштейна функциями levenshtein_r (рекурсивный алгоритм) и levenshtein (алгоритм динамического программирования) сделанный для строк различной длины с помощью программы, представленной на рис. 13. В программе поочередно вызываются функции levenshtein_r и levenshtein с одинаковыми значениями параметров и замеряется продолжительность выполнения этих функций.

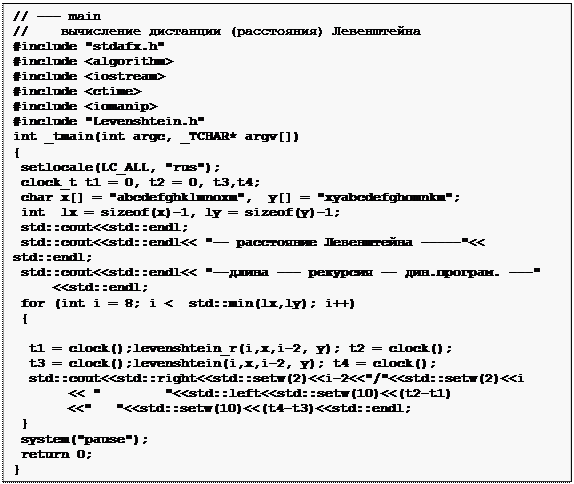
Рис. 13. Программа для сравнительного анализа продолжительности выполнения функций levenshtein_r и levenshtein

На рис. 14 представлен результат выполнения программы, приведенной на рис. 13. Продолжительность выполнения функций в распечатке приведена в миллисекундах.

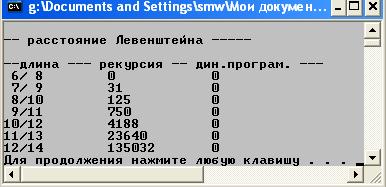
Рис. 14. Результат выполнения программы, представленной на рис. 13

Рис. 14 демонстрирует подавляющее превосходство алгоритма, основанного на динамическом программировании. При последнем просчете, в котором вычислялась дистанция Левенштейна между строками длиной 12 и 14 символов, рекурсивный алгоритм затратил на вычислении более 2 мин, а алгоритм, основанный на динамическом программировании, – менее 0,001 с.