К У Р С
Пример
char Letter_A = ‘A’;
char &ref = Letter_A;
Ссылка – псевдоним, любое изменение значения ссылки влечет изменение объекта, на который ссылка указывает
int i=0;
int &ref = i;
ref +=10; // ~ i +=10;
или
char Letter_A = ‘A’;
char &ref = Letter_A;
char Letter_B = ‘B’;
char &ref = Letter_B; // Тогда Letter_A = Letter_B
Действие со ссылкой сказывается на самом объекте. Ссылаться на тип объекта нельзя. Ссылки не могут указывать на нулевой объект (принимающий значение NULL), тогда надо использовать указатель. Использование ссылок не связано с дополнительными затратами памяти.
Пример сравнения ссылок с указателями в качестве фактических параметров
void swap(double *a, double *b)
{
double c = *a;
*a = *b;
*b = c;
}
void swap(double &a, double &b)
{
double c = a;
a = b;
b = c;
}
void main()
{
double c = 1.21;
double d = 43.1;
swap(&c, &d);
cout<<”c=”<<c<<”\t\td=”<<d<<endl;
swap(c,d);
cout<<”c=”<<c<<”\t\td=”<<d<<endl;
}
int n = -22;
void invert(int& k=n)
{
cout<<”k=”<<k<<endl;
k = -k;
}
void main()
{
int a = 21;
int b = 34l;
invert();
cout<<”n=”<<n<<endl;
invert(a);
cout<<”a=”<<a<<endl;
invert(a+b);
cout<<”a=”<<a<<”b=”<<b<<endl;
double r = 2.212;
invert(int(r));
cout<<”r=”<<r<<endl;
}
В Ы С Ш Е Й
М А Т Е М А Т И К И
Краткий конспект лекций
ЧАСТЬ 2
одной переменной.
Производная функции, ее геометрический и физический смысл.
Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.
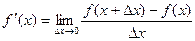
 у
у
f(x)
f(x0 +Dx) P
Df
f(x0) M
a b Dx
0 x0 x0 + Dx x
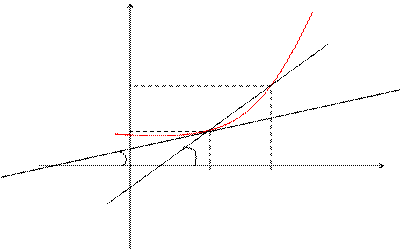
Пусть f(x) определена на некотором промежутке (a, b). Тогда 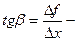 тангенс угла наклона секущей МР к графику функции.
тангенс угла наклона секущей МР к графику функции.

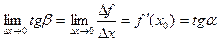 ,
,
где a - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

Уравнение касательной к кривой: 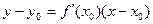

Уравнение нормали к кривой: 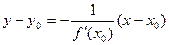 .
.
Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.
Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.
Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение.
Односторонние производные функции в точке.
Определение. Правой (левой) производной функции f(x) в точке х = х0 называется правое (левое) значение предела отношения 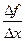 при условии, что это отношение существует.
при условии, что это отношение существует.
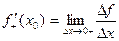
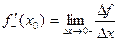
Если функция f(x) имеет производную в некоторой точке х = х0, то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во- первых функция может иметь разрыв в точке х0, а во- вторых, даже если функция непрерывна в точке х0, она может быть в ней не дифференцируема.
Например: f(x) = ïxï- имеет в точке х = 0 и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.
Теорема. (Необходимое условие существования производной) Если функция f(x) имеет производную в точке х0, то она непрерывна в этой точке.
Понятно, что это условие не является достаточным.
Основные правила дифференцирования.
Обозначим f(x) = u, g(x) = v - функции, дифференцируемые в точке х.
1) (u ± v)¢ = u¢ ± v¢
2) (u×v)¢ = u×v¢ + u¢×v
3)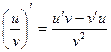 , если v ¹ 0
, если v ¹ 0
Эти правила могут быть легко доказаны на основе теорем о пределах.
Производные основных элементарных функций.
1)С¢ = 0; 9) 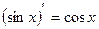
2)(xm)¢ = mxm-1; 10) 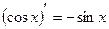
3) 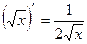 11)
11) 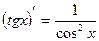
4) 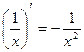 12)
12) 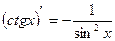
5) 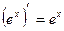 13)
13) 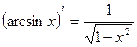
6) 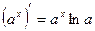 14)
14) 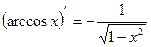
7)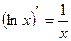 15)
15) 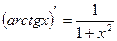
8) 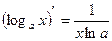 16)
16) 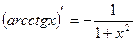
Производная сложной функции.
Теорема. Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f.

Тогда 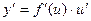
 2014-02-12
2014-02-12 332
332






