Type
Type
Type
Type
Vector = record
x1, y1, x2, y2: Integer;
Color: TColor;
End;
Для описания правильных многоугольников можно использовать следующую структуру:
TrPoligon = record
Name: String; {наименование многоугольника}
N: Integer; {количество сторон}
xс, yс: Integer; {центр описанной окружности}
R: Integer; {радиус описанной окружности}
Color: TColor;
End;
Для примитивов с переменным числом параметров, таких, как произвольные многоугольники или сплайны, переменную часть – список вершин – удобно представлять кольцевой списковой структурой на основе ссылок (рис. 2.19).
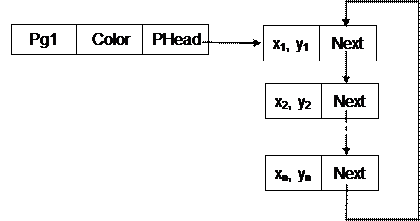 |
Рис. 2.19
Достоинством списковой структуры является простота реализации операций по добавлению в любое место списка новых элементов и удалению любых элементов из списка.
Более сложные графические объекты, синтезируемые с помощью ТМО, удобнее представить в едином формате, не зависящем от конкретных операндов и вида ТМО.
GrObject = record
Name: String; {наименование объекта}
TMO: byte; {код ТМО}
P1, P2: Pointer; {указатели на операнды ТМО}
Color: TColor;
End;
Поскольку число конечных графических объектов в процессе работы программы может меняться, их также целесообразно объединить в общий список. Для этого в приведенную выше структуру данных необходимо добавить дополнительную ссылку Next для связывания объектов.
PGrObject: ^GrObject; {тип указателей на элементы списка объектов}
GrObject = record {геометрический объект}
Name: String; {наименование объекта}
TMO: byte; {код ТМО или типа примитива}
P1, P2: Pointer; {указатели на операнды ТМО}
Next: PGrObject; {указатель на следующий объект в списке}
Color: TColor;
End;
Приведенный тип позволяет объединить в единый список и отдельные примитивы и фигуры любой сложности, полученные с помощью ТМО. Для примитивов один из указателей, например P1, необходимо использовать для ссылки на описание примитива, а второй – не использовать.
На рис. 2.20 в качестве примера организации сложной структуры приведена структура данных для объекта Fig1, иерархическая структура которого приведена на рис. 2.18, и еще одного объекта Fig2, созданного из двух примитивов. На рис. 2.20 переменная FirstPt типа PGrObject является указателем на начало списка фигур.
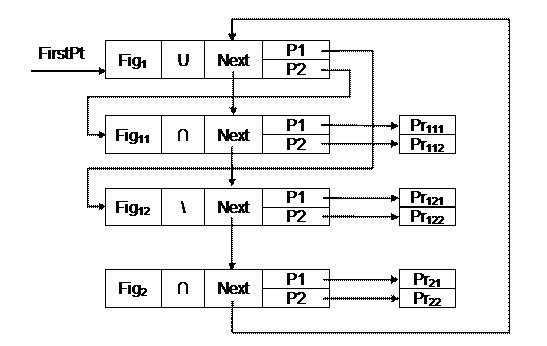
Рис. 2.20
Обычно над фигурами, полученными с помощью ТМО, также выполняются геометрические преобразования. Если для их реализации используется интегральная форма, то параметры геометрических преобразований, например матрицу результирующего преобразования, следует размещать в дополнительном поле каждого объекта типа GrObject.
Лекция 3. Геометрические преобразования
на плоскости
3.1. Двумерные геометрические преобразования
Практически всегда над объектами требуется производить преобразования, направленные на изменение их положения на плоскости, размеров или ориентации. Будем называть такие преобразования геометрическими. В математике перечисленные преобразования относятся к линейным преобразованиям над координатами (x, y) точек объектов и описываются линейными зависимостями:
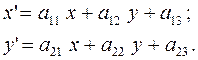 (3.1)
(3.1)
Здесь (x¢, y¢) – координаты точки (x, y) после преобразования.
Для линейных преобразований характерно то, что прямая линия преобразуется в прямую, при этом углы между прямыми могут изменяться. Наиболее распространенными видами линейных преобразований, из комбинации которых можно представить любое другое линейное преобразование, являются:
- плоскопараллельное перемещение;
- масштабирование;
- поворот.
Например, плоскопараллельное перемещение точки (x, y) на расстояние mx по оси x и на my по оси y записывается как
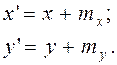 (3.2)
(3.2)
Чтобы все линейные преобразования можно было представить единообразно в матричной форме, удобно использовать применяемые в проективной геометрии однородные координаты [5, 7, 8].
Замена обычных координат однородными состоит в том, что всякой точке (x, y) на плоскости OXY можно поставить в соответствие точку в координатном пространстве OXYV с координатами (xТ, yТ, v), называемыми однородными координатами, причем 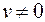 и v = const для всех точек плоскости OXY (рис. 3.1). Соответствие между обычными (декартовыми) и однородными координатами устанавливается следующим правилом преобразования однородных координат в декартовы:
и v = const для всех точек плоскости OXY (рис. 3.1). Соответствие между обычными (декартовыми) и однородными координатами устанавливается следующим правилом преобразования однородных координат в декартовы:
x = xТ / v; y = yТ / v. (3.3)
Из соотношений (3.3) следует, что все прямые, связывающие точки в однородной системе координат с соответствующими им точками на плоскости OXY, сходятся в одной точке на оси OV с координатами (0, 0, v /(1 – v)). Если возможно, то стремятся использовать значение v = 1. При этом прямые, связывающие точки в однородной и декартовой системах координат, будут параллельны оси OV, а однородные координаты xТ, yТ совпадают с обычными.
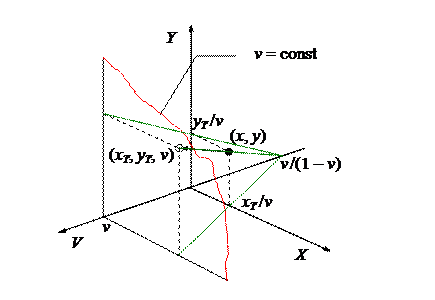
Рис. 3.1
Далее для описания геометрических преобразований будем использовать однородные координаты. В однородных координатах любое линейное геометрическое преобразование можно представить в матричной форме следующим образом:
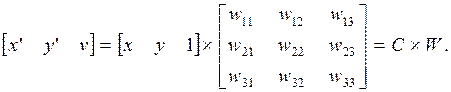 (3.4)
(3.4)
Здесь C = [ x y 1] – матрица исходных координат; C' = [ x' y' v ] – матрица новых координат после преобразования; W – матрица преобразования. Отметим, что v = 1 только для тех преобразований, в матрице W которых w 13, w 23= 0 и w 33 = 1.
Для всякого линейного преобразования существует точка, называемая центром преобразования, для которой это преобразование инвариантно, т.е. не изменяет координат этого центра.
Преобразование плоскопараллельного перемещения (сдвига) задается следующим образом:
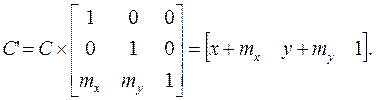 (3.5)
(3.5)
Здесь mx, my – смещения по соответствующим осям. Для плоскопараллельного перемещения центром преобразования формально считается точка 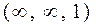 .
.
Преобразование масштабирования относительно начала координат
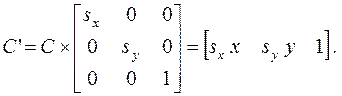 (3.6)
(3.6)
Здесь sx, sy – масштабные коэффициенты по соответствующим осям. Масштабными коэффициентами могут быть любые числа, отличные от 0. При sx, sy > 1 преобразование приводит к увеличению размеров, а при sx, sy < 1 – к уменьшению. Если sx = sy, масштабирование называется пропорциональным. При отрицательных значениях масштабных коэффициентов происходит не только изменение размеров, но и зеркальное отражение преобразуемой фигуры относительно соответствующей оси. В частности, преобразование
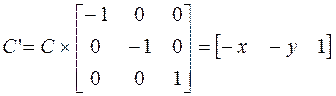 (3.7)
(3.7)
задает отражение относительно осей OX и OY, что эквивалентно повороту на 1800.
Преобразование поворота на угол 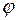 относительно начала координат
относительно начала координат
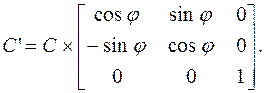 (3.8)
(3.8)
Направление поворота определяется знаком угла 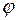 .
.
3.2. Совмещение преобразований.
Преобразование относительно заданного центра
Часто над объектами приходится последовательно выполнять несколько преобразований. Пусть последовательность преобразований задана матрицами W 1, W 2,..., Wn. Рассмотрим преобразование точки с координатами C = [ x y 1].
В результате преобразования W 1 получим
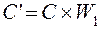 , (3.9)
, (3.9)
а после преобразования W 2
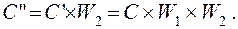 (3.10)
(3.10)
Продолжая выполнять очередные преобразования, в итоге будем иметь
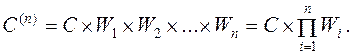 (3.11)
(3.11)
Если вычислить матрицу 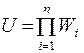 , то заданную последовательность преобразований можно заменить одним результирующим преобразованием с матрицей U.
, то заданную последовательность преобразований можно заменить одним результирующим преобразованием с матрицей U.
Замечание. Умножение матриц некоммутативно, поэтому матрицы W 1, W 2,..., Wn следует умножать в той последовательности, в которой они заданы.
Такие элементарные преобразования, как масштабирование и поворот, приведенные в форме (3.6) и (3.8), выполняются относительно начала координат. Если же преобразование W необходимо выполнить относительно произвольно заданного центра (xc, yc), то его производят в следующей последовательности.
1. Заданную точку P с матрицей координат С и центр преобразования сместить преобразованием M так, чтобы центр преобразования совпал с началом координат:
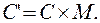 (3.12)
(3.12)
2. Выполнить над P заданное преобразование W относительно начала координат, а следовательно, и относительно заданного центра преобразования:
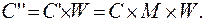 (3.13)
(3.13)
3. Обратным преобразованием перемещения M -1 точку и центр преобразования сместить так, чтобы центр преобразования снова оказался на исходном месте:
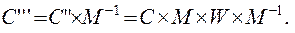 (3.14)
(3.14)
Матрица преобразования смещения M и обратная ей матрица M -1имеют следующий вид:
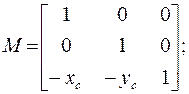
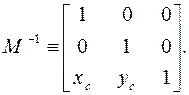 (3.15)
(3.15)
Таким образом, матрица U результирующего преобразования относительно заданного центра вычисляется как
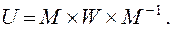 (3.16)
(3.16)
Предварительный расчет матрицы U перед выполнением преобразования позволяет сократить объем вычислений при расчете новых координат точек.
3.3. Преобразование алгебраических линий
Линейные геометрические преобразования можно применять не только к отдельным точкам, но и к другим объектам, имеющим аналитическое описание. В частности, можно производить преобразование алгебраических линий.
Уравнение прямой линии общего положения
a 1 x + a 2 y + a 3 = 0 (3.17)
представим в матричной форме:
C ´ A = 0, (3.18)
где C º 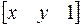 , A º
, A º 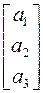 .
.
Пусть над линией необходимо выполнить преобразование с матрицей W, т.е. всякой точке на прямой с матрицей исходных координат С нужно поставить в соответствие точку с матрицей координат C ¢ = C ´ W.
Из последнего соотношения выразим C. Для этого умножим обе части равенства на матрицу W -1, обратную матрице W:
C ¢ ´ W -1 = C ´ W ´ W –1. (3.19)
После сокращения получим С = C ¢ ´ W –1. Подставим выражение для C в исходное уравнение прямой (3.17):
C ¢ ´ W -1 ´ А = 0. (3.20)
Поскольку C¢ – матрица координат после преобразования, то уравнение (3.20) будет соответствовать той же прямой после преобразования, а W -1 ´ А – это матрица-столбец коэффициентов уравнения прямой после преобразования, т.е. для преобразования с матрицей W формула для расчета матрицы A¢ новых коэффициентов уравнения прямой имеет следующий вид:
A¢ = W -1 ´ А. (3.21)
Рассмотрим теперь преобразование линии 2-го порядка общего вида с уравнением
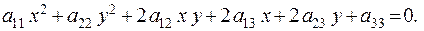 (3.22)
(3.22)
Представим (3.22) в матричной форме:
C ´ A ´ C Т = 0, (3.23)
где 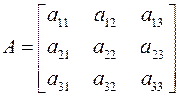 – матрица коэффициентов уравнения линии. Причем матрица A симметрическая, т.е. aij = aji для i, j = 1, 2, 3. Матрица-столбец C Т означает транспонированную матрицу C.
– матрица коэффициентов уравнения линии. Причем матрица A симметрическая, т.е. aij = aji для i, j = 1, 2, 3. Матрица-столбец C Т означает транспонированную матрицу C.
Как и в предыдущем случае, сделаем в уравнении (3.23) замену С = C ¢ ´ W –1. В результате получим
С¢ ´ W –1 ´ A ´ (C ¢ ´ W –1) T = 0. (3.24)
Чтобы привести (3.24) по форме к первоначальному виду, воспользуемся следующей известной в математике формулой о транспонировании произведения матриц:(C ¢ ´ W –1) T = (W –1) T ´ (C ¢) T. На основании нее уравнение (3.24) можно представить следующим образом:
С¢ ´ W –1 ´ A ´ (W –1) T ´ (C ¢) T = 0. (3.25)
Сравнивая (3.23) и (3.25), можно заключить, что W –1 ´ A ´ (W –1) T должно быть матрицей коэффициентов уравнения линии. Следовательно, формула для вычисления новых коэффициентов уравнения линии 2-го порядка после преобразования W будет иметь следующий вид:
A¢ = W –1 ´ A ´ (W –1) T. (3.26)
Приведенные здесь выводы позволяют производить геометрические преобразования над любыми объектами, заданными в аналитическом виде.
3.4. Непрерывные геометрические преобразования
Непрерывные геометрические преобразования – важный инструмент в интерактивных графических программах, с помощью которого производится построение и размещение фигур на экране монитора. Другим применением непрерывных преобразований является анимация, т.е. моделирование различных видов движения объектов по заранее разработанным траекториям или других непрерывных изменений их геометрии.
В силу дискретного характера формирования изображения в компьютере плавные, непрерывные преобразования получают как последовательность малых преобразований. Результат каждого преобразования, как кадр фильма, выводится на экран.
Реализация непрерывных преобразований возможна в двух формах – интегральной и дифференциальной.
В интегральной форме в любой момент времени t матрица С (t) текущих координат рассчитывается на основе матрицы С 0 исходных, т.е. первоначально заданных и неизменяемых координат:
C (t) = C 0 ´ W (t), (3.27)
где W (t) – матрица текущего преобразования на момент времени t.
Начальным значением матрицы W (t) для t = 0 будет единичная матрица I, т.е. W (0) = I.
В дифференциальной форме для расчета матрицы С(t + ∆t) новых координат на очередном шаге преобразования используется матрица С(t) координат, полученных на предыдущем шаге:
C (t + ∆t) = C (t) ´ ∆W, (3.28)
где ∆W – матрица элементарно малого преобразования за время ∆t.
Начальным значением С (t) при t = 0 будет матрица первоначально заданных координат, т.е. С (0) = C 0.
В программах, моделирующих движение объектов в реальных условиях, параметры t и ∆t соответствуют времени. В большинстве же других графических приложений более важным бывает сам факт движения объектов. Тогда в качестве величины, сопоставимой со временем, удобнее использовать программные циклы по расчету результатов элементарных преобразований и визуализации, т.е. t в этом случае будет соответствовать номеру цикла, а ∆t =1.
Ниже показано, как в интегральной форме выглядят частные виды непрерывных преобразований.
Преобразование плоскопараллельного перемещения
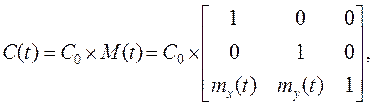 (3.29)
(3.29)
где mx (t) и my (t) – функции, задающие непрерывное перемещение по соответствующим осям. Для равномерного прямолинейного перемещения mx (t)= vxt; my (t) = vy t, где vx,vy – составляющие скорости [1/цикл].
Преобразование вращения относительно начала координат
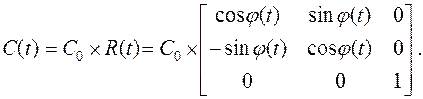 (3.30)
(3.30)
Функция 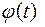 определяет непрерывное изменение угла поворота. Для моделирования равномерного вращения
определяет непрерывное изменение угла поворота. Для моделирования равномерного вращения 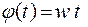 следует задать угловую скорость w [рад/цикл].
следует задать угловую скорость w [рад/цикл].
Преобразование масштабирования относительно начала координат
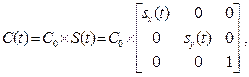 (3.31)
(3.31)
где sx (t) и sy (t) – функции, задающие непрерывное изменение масштабных коэффициентов по соответствующим осям. Для моделирования линейного изменения масштабов по осям со скоростями vx и vy формулы изменения масштабных коэффициентов будут следующими:
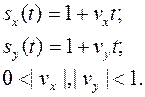 (3.32)
(3.32)
При программной реализации этого закона необходимо контролировать и не допускать использование нулевых значений sx (t) и sy (t), приводящих к вырождению преобразуемых объектов.
Эффекту приближения и удаления фигур лучше соответствует показательный закон изменения масштаба:
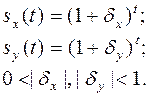 (3.33)
(3.33)
Этот закон удобен и в реализации, так как нулевые значения sx (t) и sy (t) здесь исключаются.
Простейшие законы изменения параметров в приведенных непрерывных преобразованиях даны в качестве примеров. Если необходимо, то можно использовать и более сложные законы, в том числе и задаваемые с помощью различных средств ввода: мыши, джойстика, трекбола и других устройств управления или контроля. Например, в системах виртуальной реальности значения этих параметров поступают с датчиков, контролирующих движения пользователя.
Теперь рассмотрим, как выглядят непрерывные преобразования в дифференциальной форме.
Плоскопараллельное перемещение:
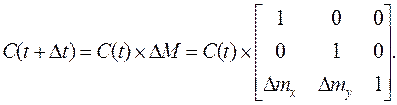 (3.34)
(3.34)
Здесь ∆mx, ∆my – элементарно малые перемещения по соответствующим осям за время ∆t.
Вращение вокруг начала координат:
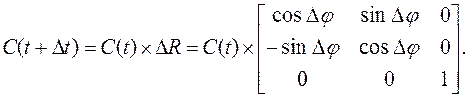 (3.35)
(3.35)
Здесь ∆φ – элементарно малый угол поворота за время ∆t.
Масштабирование относительно начала координат:
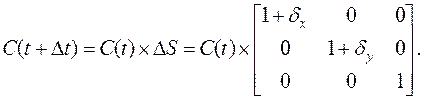 (3.36)
(3.36)
Здесь (1 + δx), (1 + δy) – элементарно малые изменения масштабных коэффициентов.
Заметим, что моделирование масштабирования в дифференциальной форме по результату соответствует масштабированию в интегральной форме на основе показательного закона изменения масштабных коэффициентов.
Сравнивая между собой интегральную и дифференциальную формы геометрических преобразований, можно сделать следующие выводы:
- в дифференциальной форме ошибки от каждого элементарного преобразования со временем накапливаются в значениях координат, что при большом числе шагов преобразования может привести к отклонению от заданной траектории и к необратимым искажениям формы фигур;
- в интегральной форме легко задавать различные законы изменения параметров;
- в дифференциальной форме легко реализуются только линейные законы изменения параметров (для масштабирования – показательный).
3.5. Линейные преобразования
фрагментов изображения
При работе с готовыми растровыми изображениями часто возникает необходимость в преобразовании какого-либо выделенного фрагмента изображения в другую заданную область. Исходное и результирующее изображения могут размещаться либо непосредственно в видеопамяти, либо в оперативной памяти (обычно в формате bitmap).
Рассмотрим вначале частный случай, когда обе области – исходная Im 1 и новая Im 2 ограничены параллелограммами, причем ориентация и размеры параллелограммов могут быть различными (рис. 3.2).
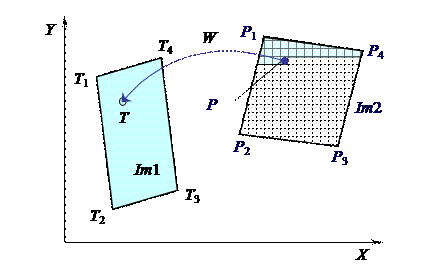
Рис. 3.2
Для задания области Im 1 достаточно указать три вершины параллелограмма, например T 1, T 2 и T 3. Координаты вершины T 4 при необходимости несложно рассчитать по точкам T 1, T 2 и T 3. Область Im 2 также должна быть задана тройкой вершин P 1, P 2, P 3, соответствующих вершинам T 1, T 2, T 3. Координаты точки Р 4. можно найти по координатам точек P 1, P 2, P 3.
Если иметь преобразование W, ставящее в соответствие всякой точке P из Im 2 точку T из Im 1 (см. рис. 3.2), то поставленную задачу можно решить путем построчного сканирования области Im 2, в процессе которого для каждой точки P с целочисленными координатами из Im 2 с помощью W находится соответствующая точка T в Im 1. Когда точка T найдена ее цветом нужно закрасить точку P.
Для наглядности матрицы-строки однородных координат точек T 1, T 2, T 2, P 1, P 2, P 3 будем обозначать так же, как и сами точки:
T 1 = [ xT 1 yT 1 1], T 2 = [ xT 2 yT 2 1], T 3 = [ xT 3 yT 3 1];
P 1 = [ xP 1 yP 1 1], P 2 = [ xP 2 yP 2 1], P 3 = [ xP 3 yP 3 1].
Преобразование W должно быть единым для всех точек области прибытия Im 2, в том числе и для точек P 1, P 2, P 3, соответствующих точкам T 1, T 2, T 3. Поэтому
T 1 = P 1 ´ W; (3.37)
T 2 = P 2 ´ W; (3.38)
T 3 = P 3´ W. (3.39)
Отметим, что преобразование W должно возвращать значение координаты v =1.
Чтобы найти W, объединим соотношения (3.37) – (3.39) в общую формулу:
Mt = Mp ´ W, (3.40)
где 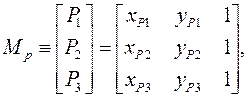
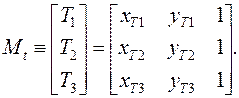
Умножим слева обе части уравнения (3.40) на матрицу Mp -1, обратную матрице Mp:
Mp -1´ Mt = Mp -1´ Mp ´ W. (3.41)
В результате получим формулу для вычисления коэффициентов матрицы W искомого преобразования:
W = Mp -1 ´ Mt. (3.42)
Ниже приводится алгоритм преобразования фрагмента изображения из области Im 1 в область Im 2.
1. Последовательно просматривая список вершин (P 1, P 2, P 3, P 4)области прибытия, найти границы ее сканирования Ymin и Ymax.
2. Для каждой строки Y из [ Ymin.. Ymax ] выполнить пп. 2.1 – 2.2.
2.1. Найти координаты xl и xr левой и правой точек пересечения области Im 2 со строкой Y.
2.2. Для каждого целого X из [ xl.. xr ]выполнить пп. 2.2.1– 2.2.2.
2.2.1. Преобразовать с помощью преобразования W точку P = (X, Y)области Im 2в область Im 1, т.е. вычислить координаты (X 1, Y 1) соответствующей точки T.
2.2.2. Считать код цвета точки T и переписать его в точку P.
Данный алгоритм гарантированно заполняет новую область Im 2пикселями из Im 1без пропусков и повторений. При его реализации следует учитывать, что при хотя бы частичном наложении Im 1 и Im 2, размещающихся в общей области памяти, корректность работы алгоритма может нарушиться из-за попадания точек области Im 2 в область Im 1 и возможности включения их в производимые преобразования.
В рассмотренном частном случае выполнялось преобразование фрагмента изображения, ограниченного параллелограммом. Однако преобразованию (3.42) можно подвергнуть и все исходное изображение. Для вычисления матрицы W в этом случае нужно лишь задать на исходном изображении любую тройку точек, не лежащих на одной прямой, и поставить им в соответствие три точки результирующей области.
Лекция 4. Трехмерная компьютерная графика
4.1. Трехмерные примитивы
Предметом трехмерной компьютерной графики являются различные пространственные объекты. По геометрическим свойствам их можно разделить на следующие виды:
- точки в пространстве;
- пространственные линии и отрезки линий;
- поверхности;
- многогранники;
- геометрические тела сложной формы.
Для синтеза реалистичных изображений кроме геометрии объектов необходимо также моделировать распространение света, что заставляет задавать и использовать ряд физических свойств объектов и всей пространственной сцены. К ним относятся расположение и яркость источников света, цвета и степень зеркальности (гладкости) поверхностей объектов, коэффициенты преломления света на границах прозрачных сред, степень их прозрачности и др.
Геометрия трехмерных примитивов, как и двумерных, описывается алгебраическим и параметрическим методами. Ниже в качестве примитивов будут рассмотрены точки, линии, поверхности и многогранники.
Tочка P в пространстве задается своими координатами (x, y, z). В трехмерной компьютерной графике традиционно используют левостороннюю систему координат, показанную на рис. 4.1. Причем изображение строится на плоскости OXY, называемой картинной плоскостью. На нее проецируются изображаемые объекты.
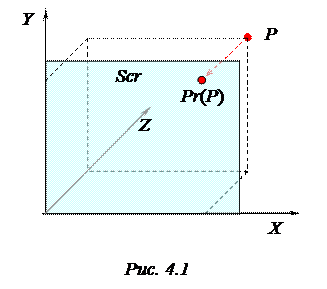 На рис. 4.1 Pr (P) означает проекцию точки P на картинную плоскость. Часть этой плоскости, соответствующая экрану монитора, обозначена как Scr.
На рис. 4.1 Pr (P) означает проекцию точки P на картинную плоскость. Часть этой плоскости, соответствующая экрану монитора, обозначена как Scr.
Для задания линий в пространстве используется алгебраическая и параметрическая формы.
В алгебраической форме линия в пространстве задается как пересечение двух поверхностей, что представляется в виде системы алгебраических уравнений
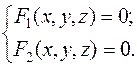 (4.1)
(4.1)
Пространственные кривые в параметрической форме отличаются от плоских, рассмотренных в п. 2.3, 2.4, лишь тем, что изменение координаты z задается третьей функция z (t):
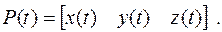 (4.2)
(4.2)
Формулы и выводы, приведенные в п. 2.3, 2.4, несложно модифицировать для описания кубических сплайнов и кривых Безье в пространстве.
Поверхности, как и линии, задаются в алгебраической и параметрической формах. Алгебраическая поверхность описывается уравнением вида F (x, y, z) = 0. Например, уравнение сферической поверхности с центром в начале координат и радиусом R имеет вид
x 2 + y 2 + z 2 – R 2 = 0. (4.3)
В параметрической форме задаются четырехугольные куски S (u,v)произвольных гладких поверхностей (рис. 4.2). Закон изменения каждой из координат поверхности должен быть описан своей функцией от двух параметров u и v:
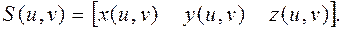 (4.4)
(4.4)
Как и для параметрических кривых, в качестве области изменения параметров u и v обычно используют интервал [0, 1], т.е. 0 £ u £ 1, 0 £ v £ 1.
 |
Рис. 4.2
При интерактивном синтезе параметрических поверхностей для функций x (u, v), y (u, v) и z (u, v) используют те же полиномиальные базисы, что и в двумерной графике. Разработаны математическая теория и алгоритмы для создания полиномиальных кубических поверхностей, поверхностей Безье и других видов полиномиальных сплайн-поверхностей [7, 8].
В то же время для задания некоторых видов поверхностей удобнее использовать другие базисы. Так, особым классом поверхностей являются поверхности вращения [7]. Поверхностью вращения называется поверхность, образованная вращением плоской кривой вокруг неподвижной оси, лежащей в одной плоскости с кривой. Например, функция
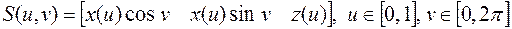 (4.5)
(4.5)
определяет поверхность, описанную вращением кривой P (u)= [ x (u) z (u)], заданной в плоскости OXZ, вокруг оси OZ (рис. 4.3).
 |
Рис. 4.3
Другим примером поверхности вращения может служить сферическая поверхность радиусом R с центром в начале координат, описываемая следующим образом:
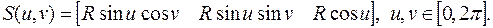 (4.6)
(4.6)
Отметим, что параметры u и v определяют на поверхности географическую систему координат, в которой u является долготой, а v – широтой. Полюса этой сферы расположены на оси OZ.
4.2. Аппроксимация криволинейных поверхностей
Представление криволинейной поверхности в параметрической форме S (u, v) позволяет визуализировать ее с любой точностью и детальностью. Однако прямые вычисления значений функций x (u, v), y (u, v) и z (u, v) в общем случае весьма трудоемки, поэтому при разработке быстрых алгоритмов визуализации параметрические поверхности предварительно подвергают полигональной аппроксимации, т.е. криволинейную поверхность заменяют многогранной поверхностью из плоских многоугольников. Общепринято аппроксимировать криволинейные поверхности плоскими треугольниками. На рис. 4.4 показан результат такой аппроксимации для поверхности, изображенной на рис. 4.2.
 |
Рис. 4.4
Основная процедура аппроксимации состоит в расчете узловых точек поверхности S (u, v), т.е. точек, которые будут использоваться в качестве вершин аппроксимирующих треугольников. Для этого выполняют табуляцию S (u, v) по обоим параметрам u и v. Шаги табуляции D u иD v чаще выбирают постоянными. В итоге заполняется двумерный массив V координат узловых точек. Элемент V [ i, j ] массива – это координаты (x, y, z) точки поверхности S (u, v), вычисленные для значений параметров u = i D u и v = j D v.
Модель криволинейной поверхности в форме массива V, получившаяся в результате линейной аппроксимации, называется полигональной [8]. В дальнейшем при формировании изображения рассматривается множество примыкающих к друг другу треугольников, вершины, которых хранятся в массиве V.
4.3. Многогранники и сложные объекты
Кусок параметрической поверхности S (u, v) может быть замкнутым. Примером может служить сфера. После аппроксимации замкнутой поверхности получится поверхность, ограничивающая геометрическое тело в виде многогранника. Многогранники часто выделяются в самостоятельный вид трехмерных примитивов. Произвольный многогранник Mg, ограниченный n гранями, описывается списком граней, т.е. плоских многоугольников:
Mg = (G 1, G 2, …, Gn).(4.7)
Каждая грань Gi в свою очередь задается упорядоченным списком вершин:
Gi = (Pi 1, Pi 2, …, Pim). (4.8)
Частным случаем многогранников являются правильные многогранники, т.е. многогранники с одинаковыми гранями в виде правильных многоугольников [4]. Примером правильных многогранников является гексаэдр, обычно называемый кубом
(рис. 4.5). Его геометрия задается одним параметром – длиной ребра.
Правильные многогранники вписываются в сферическую поверхность. Характеризуются количеством n граней и числом m сторон граней. Всего существует лишь пять видов правильных многогранников, называемых также Платоновыми телами: тетраэдр (n = 4, m = 3), гексаэдр (n = 6, m = 4), октаэдр (n = 8, m = 3), икосаэдр (n = 20, m = 3), додекаэдр (n = 12, m = 5). Для описания правильного многогранника достаточно задать координаты (xc, yc, zc) центра и радиус R описанной сферической поверхности, а также значения m и n. Для каждого вида правильных многогранников существуют свои алгоритмы расчета координат вершин по этим данным [4].
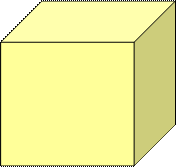 |
| Рис. 4.5 | Рис. 4.6 |
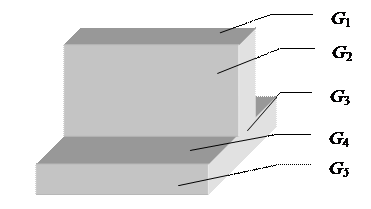
Математическое описание и визуализация трехмерных объектов сложной формы, поверхность S которых состоит из граней в виде кусков алгебраических или параметрических поверхностей, представляет определенную проблему. На рис. 4.6 приведен пример сложного объекта с плоскими гранями и обозначены его видимые грани.
Очевидным подходом к описанию сложного геометрического объекта по аналогии с многогранниками является представление его поверхности списком граней S = (G 1, G 2, …, Gm). Описание каждой грани Gi в свою очередь должно включать описание поверхности, частью которой является грань, и описание граничного контура, т.е. отрезков всех линий пересечения данной грани со смежными гранями. Однако независимое конструирование граней для сборки их в одну поверхность с гарантией их точного сопряжения трудно реализовать практически, что и ограничивает применение этого подхода.
Как и в двумерной графике, для конструирования сложных пространственных объектов из примитивов можно использовать теоретико-множественные операции (ТМО). Однако программная реализация пространственных ТМО по сравнению с двумерными значительно сложнее. Единственной операцией, которая реализуется естественным образом без дополнительных расчетов, является объединение геометрических тел, поэтому при разработке недорогих графических систем часто выбирают компромиссное решение, когда сложные объекты собираются путем объединения заготовок более простых форм. Заготовки фактически являются расширением набора примитивов формами, характерными для конкретной прикладной области. Например, типичными заготовками для машиностроительных систем автоматизированного проектирования (САПР) являются цилиндры, конусы, параллелепипеды, шестигранники, пирамиды и т.п.
4.4. Свет и цвет
Для трехмерной компьютерной графики основополагающими являются понятия света и цвета. Свет – это электромагнитное излучение, воспринимаемое человеческим зрением. Видимый свет занимает участок спектра электромагнитного излучения с длинами волн от 400 до 700 нм. Свет излучается источниками света и характеризуется яркостью и цветом. Свет одной длины волны имеет определенный цвет и называется монохроматическим. Обычно источник света излучает поток световых волн с разными длинами и амплитудами. В белом свете присутствуют световые волны всего видимого спектра. В остальных случаях свет имеет цвет, определяемый доминирующими длинами волн в световом потоке.
Для правильного понимания физической сущности природы света кратко рассмотрим основные светотехнические величины и единицы измерения [1].
Световой поток F характеризует мощность светового излучения, проходящего на элемент поверхности площадью S, освещаемый источником света. Измеряется в люменах (лм). Полный световой поток Fc равен мощности светового излучения сквозь произвольную замкнутую поверхность, охватывающую источник света.
В общем случае источник света излучает его неравномерно по разным направлениям. Плотность светового потока в телесном угле выбранного направления называется силой света. Она находится как
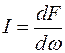 , (4.9)
, (4.9)
где w – телесный угол с центром в источнике света.
Для точечного источника света, излучающего свет равномерно по всем направлениям, сила света находится как
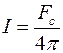 . (4.10)
. (4.10)
Единица измерения силы света называется канделла (кд, [кд] = [лм/ср]).
Освещенностью E элемента поверхности называется отношение приходящегося на нее светового потока dF к ее площади dS:
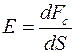 . (4.11)
. (4.11)
Единица измерения освещенности называется люкс (лк, [лк] = [лм/м2]).
Яркостью B источника называется поверхностная плотность силы света в заданном направлении. Яркость находится как отношение силы света к площади проекции светящейся поверхности на плоскость, перпендикулярную к этому направлению:
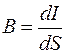 , (4.12)
, (4.12)
где dS – площадь проекции элемента светящейся поверхности. Яркость измеряется в единицах кд/м2.
В компьютерной графике наиболее популярной моделью представления света является аддитивная модель, сокращенно обозначаемая как RGB [3]. Это обозначение образуется начальными буквами трех основных цветов: красного (r ed), зеленого (g reen) и синего (b lue). В аддитивной модели считается, что любой свет образуется за счет смешения трех основных цветовых составляющих – красной, зеленой и синей. Отметим, что смешение света трех основных цветов используется и при формировании изображения на экране мониторов.
При использовании RGB модели обозначать яркость источника света, как и в физике, буквой B неудобно, поскольку она же используется для обозначения синего цвета, поэтому, как и в большинстве публикаций по компьютерной графике, для обозначения яркости в дальнейшем будем использовать букву E. Тогда в аддитивной модели источник света будет характеризоваться цветовыми составляющими – красной ER, зеленой EG и синей EB. Яркость источника белого света можно задавать одной величиной E. При этом считается, что яркости всех трех цветовых компонент белого света равны друг другу.
Основными видами идеализированных источников света являются точечный и бесконечно удаленный.
Точечный источник света помимо цветовых компонент яркости характеризуется еще координатами (xe, ye, ze) его расположения. В этом случае для всякой точки (x, y, z) освещаемой поверхности направление излучаемого света определяется координатами источника и этой точки. Бесконечно удаленный источник света излучает параллельные лучи света, направление которых всюду определяется вектором Ve = (vxe, vye, vze).
Еще одно отличие компьютерной графики от физики состоит в том, что яркость моделируемых источников света, как правило, задается не в физических, а в относительных единицах. Обычно используется ограниченный диапазон целых чисел, например 0..255, используемый при кодировании компонент цвета в RGB модели.
Зрение основано на том, что свет от источников освещает поверхности предметов, которые частично отражают его. Часть отраженного света попадает в глаз, что позволяет сформировать представление о геометрии предметов и цвете их поверхностей. Этот же принцип используется в фото– и видеоаппаратуре, а также при машинном синтезе изображений виртуальных сцен, поэтому для компьютерной графики наиболее важной физической характеристикой поверхности является ее цвет, который характеризует отражательную способность поверхности в разных областях спектра белого света. В цветовой модели RGB цвет поверхности также задается цветовыми компонентами R, G и B, но, в отличие от света, значения R, G и B характеризуют отражательную способность поверхности соответственно для красной, зеленой и синей составляющих света. В компьютерных программах значения R, G и B для вычислений удобнее задавать в диапазоне от 0 до 1 или в процентах.
Кроме RGB используются и иные цветовые модели с другими методами образования необходимых цветов из фиксированного набора основных. Так, в субтрактивной модели CMY тоже используются три основных цвета – голубой (c yan), пурпурный (m agenta) и желтый (y ellow) [1, 3]. Эти цвета считаются дополнительными соответственно к красному, зеленому и синему цветам модели RGB, т.е. могут быть получены вычитанием из белого соответственно красного, зеленого и синего цветов. Модель CMY первоначально использовалась в полиграфии при печати цветных изображений на белой бумаге, поскольку она хорошо отражает получение новых цветов при смешивании красок.
Модификацией CMY является расширенная субтрактивная модель, обозначаемая как CMYK. В этой модели используется еще один цвет – черный, а буква K в обозначении соответствует последней букве в слове black – черный. Добавление черного цвета связано с тем, что смешиванием красок трех дополнительных цветов трудно добиться чисто черного цвета.
Существуют соотношения, позволяющие преобразовывать CMYK -модель в RGB и наоборот [1].
4.5. Диффузная модель распространения света
Диффузная модель распространения света [6, 8] является одной из наиболее простых. В ней поверхности тел рассматриваются как идеальные рассеиватели света, рассеивающие падающий на них свет равномерно по всем направлениям. Тогда согласно закону Ламберта (закон косинусов) яркость света, отражаемого в направлении плоскости проекции (в направлении наблюдателя), пропорциональна косинусу угла между нормальным вектором N к поверхности и вектором L направления на источник света (рис. 4.7).
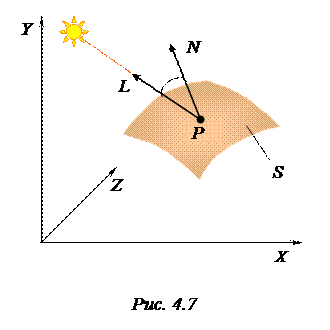 Для более детального знакомства с диффузной моделью рассмотрим элемент произвольной поверхности S, которая освещается источником света с яркостью цветовых составляющих ER, EG и EB.
Для более детального знакомства с диффузной моделью рассмотрим элемент произвольной поверхности S, которая освещается источником света с яркостью цветовых составляющих ER, EG и EB.
Если рассматривается бесконечно удаленный источник света, то L = – Ve. При точечном источнике света вектор L для каждой точки P поверхности S приходится рассчитывать через координаты этой точки и координаты источника.
Косинус угла между нормальным вектором N к поверхности и вектором L можно найти как скалярное произведение этих векторов после приведения их к единичной длине (нормирования).
Нормальный вектор N к поверхности, заданной уравнением
F (x, y, z) = 0,находится с помощью частных производных:
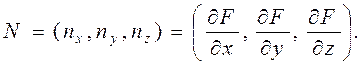 (4.13)
(4.13)
Выполним его нормирование:
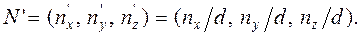 (4.14)
(4.14)
Здесь d – евклидова норма (длина) вектора N, которая находится следующим образом:
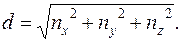 (4.15)
(4.15)
Будем считать, что вектор L уже нормирован. Скалярное произведение векторов N' и L обозначается как (N' ∙ L) и вычисляется по формуле
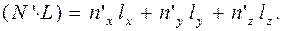 (4.16)
(4.16)
В итоге для диффузной модели цветовые компоненты света, отраженного в направлении плоскости проекции (наблюдателя), рассчитываются следующим образом:
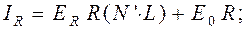 (4.17)
(4.17)
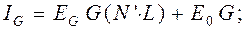 (4.18)
(4.18)
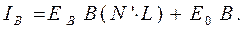 (4.19)
(4.19)
Переменная E 0 в формулах (4.17) – (4.19) обозначает яркость рассеянного белого света. В данной модели она упрощенно учитывает тот факт, что в реальной действительности кроме направленных лучей света, падающих от источников, всегда присутствует свет, равномерно рассеянный по разным направлениям. Рассеяние света происходит как в среде распространения света (обычно в воздухе), так и за счет многократного отражения света от поверхностей окружающих предметов. Составляющая E 0позволяет регулировать контрастность формируемого изображения.
В приведенных формулах считается, что яркость E света источника всюду постоянна, что справедливо лишь для бесконечно удаленных источников. Если же используется точечный источник, расположенный на конечном расстоянии от рассматриваемой сцены, то необходимо учитывать, что реальная яркость Ere света снижается с увеличением расстояния d от источника до элемента поверхности. Эта зависимость имеет следующий вид:
Ere = E /(d + c), (4.20)
где c – постоянная, задаваемая опытным путем. Формула применима как для белого, так и для компонент цветного света.
Следует отметить, что при разработке программ значения E, ER, EG, EB, E 0 можно задавать как реальные физические величины в соответствующих единицах измерения яркости, но при выводе изображения вычисленные величины IR, IG, IB должны быть приведены путем нормирования к диапазону значений в используемой цветовой палитре компьютера. В силу сказанного в программах трехмерной графики яркости источников и рассеянного света чаще задают в условных единицах.
4.6. Зеркальное отражение света
В диффузной модели предполагалось, что свет, падающий от источников на поверхности объектов, отражается равномерно по всем направлениям, в том числе и в направлении плоскости проекций. Эта модель хорошо соответствует реальным объектам с матовой поверхностью, однако поверхности многих предметов, особенно металлических, обладают ярко выраженными зеркальными свойствами. Для них наибольшая доля света рассеивается от поверхности в соответствии с законом зеркального отражения: угол падения равен углу отражения (рис. 4.8). Модели распространения света, учитывающие зеркальные свойства поверхностей, называются рефлексными [8].
На рис. 4.8 L – вектор направления на источник света; N – нормальный вектор к поверхности.
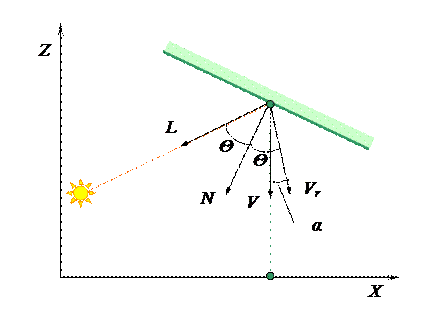
Рис. 4.8
Яркость света, отраженного в направлении V плоскости проекции, зависит от величины угла α между вектором Vr направления зеркального отражения и вектором V. Эта зависимость различна для разных материалов и гладкости их поверхности. Для реальных материалов она определяется экспериментально. При машинном же синтезе изображений виртуальных объектов для качественного моделирования зеркальности чаще используют эмпирические модели. Так, в рефлексной модели, предложенной Фонгом [1, 5], интенсивность света, отраженного в направлении вектора V, считается пропорциональной величине сos n α, где n – коэффициент зеркальности. На практике значение n выбирают в диапазоне 1 – 200.
Если векторы Vr и V уже нормированы, то сos α можно рассчитать как скалярное произведение этих векторов, т.е. 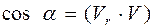 . Тогда формулы для расчета значений цветовых компонент света, отраженного в направлении плоскости проекции (наблюдателя), примут следующий вид:
. Тогда формулы для расчета значений цветовых компонент света, отраженного в направлении плоскости проекции (наблюдателя), примут следующий вид:
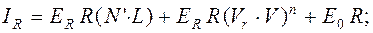 (4.21)
(4.21)
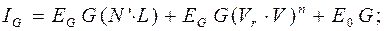 (4.22)
(4.22)
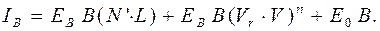 (4.23)
(4.23)
Формулы (4.21) – (4.23) отражают обе модели распространения света – диффузную и рефлексную.
4.7. Трехмерные геометрические преобразования
Так же, как и в двумерной графике, при интерактивной работе с трехмерными объектами над ними приходится производить различные геометрические преобразования. Трехмерные линейные преобразования в однородных координатах отличаются от двумерных только числом координат и размерностью матриц преобразования, равной 4 x 4.
В общем виде линейное трехмерное преобразование с матрицей W в однородных координатах x, y, z, v представляется следующим образом:
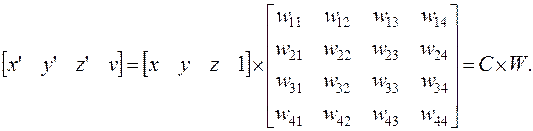 (4.24)
(4.24)
Здесь C = [ x y z 1] – матрица исходных координат; C’ = [ x' y' z' v ] – матрица новых координат после преобразования.
Важно иметь в виду, что значение координаты v остается равным 1 только в таких преобразованиях, для которых w 14, w 24, w 34 = 0 и
w 44 = 1. В противном случае для перехода к обычной системе координат необходимо выполнить пересчет:
x = x' / v; y = y' / v; z = z' / v. (4.25)
Приведем формулы для основных видов геометрических преобразований в пространстве.
Преобразование перемещения
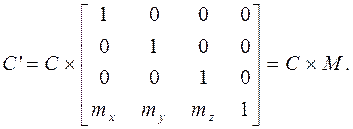 (4.26)
(4.26)
Здесь mx, my, mz – составляющие перемещения по соответствующим осям.
Преобразование масштабирования относительно начала координат
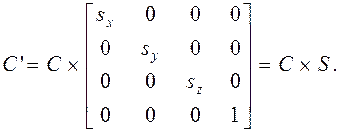 (4.27)
(4.27)
Здесь sx, sy, sz – масштабные коэффициенты по соответствующим осям. Ограничения на значения масштабных коэффициентов здесь те же, что и для двумерного случая.
Преобразование поворота относительно оси OX на угол φ
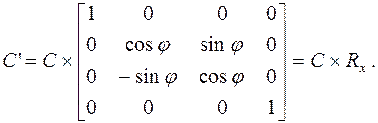 (4.28)
(4.28)
Преобразование поворота относительно оси OY на угол φ
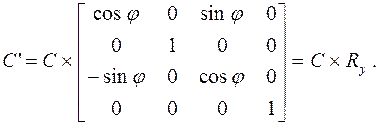 (4.29)
(4.29)
Преобразование поворота относительно оси OZ на угол φ
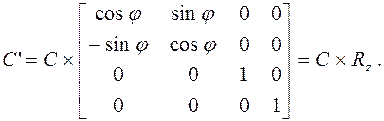 (4.30)
(4.30)
Стоит отметить, что формула (4.5) в п. 4.1 для поверхности вращения получена путем применения преобразования вращения вокруг оси OZ к кривой, заданной параметрической функцией P (u).
Для выполнения трехмерных преобразований относительно заданного центра сначала его следует совместить с началом координат, затем выполнить заданное преобразование относительно начала координат, а после этого сместить объект и центр в исходное положение.
4.8. Проецирование трехмерных объектов
Целью визуализации является синтез изображения в виде проекции объектов пространственной сцены, поэтому проецирование является важным этапом процесса визуализации. Это преобразование каждой точке P поверхности ставит в соответствие ее проекцию, т.е. точку Pr (P) на плоскости проекций.
Обычно используют один из двух следующих видов проецирования – параллельное и центральное (перспективное).
При параллельном проецировании все линии проецирования параллельны между собой. Наиболее простым частным вариантом параллельного проецирования является ортогональное проецирование (рис. 4.9), в котором линии проецирования перпендикулярны плоскости проекций.
В системе однородных координат ортогональное проецирование на плоскость OXY представляется как преобразование координат C = [ x y z 1] с вырожденной матрицей преобразования:
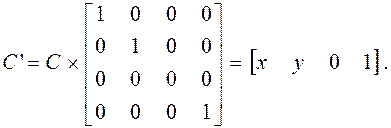 (4.31)
(4.31)
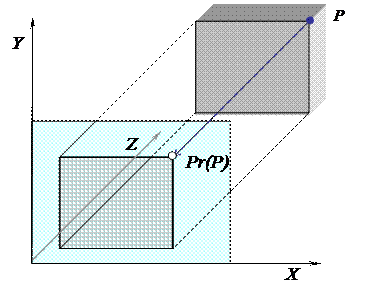 |
Рис. 4.9
Практически же, как это следует из (4.31), для получения координат C' точек Pr (P) проекции в данном случае достаточно отбросить координаты z проецируемых точек P.
Ортогональное проецирование широко используется в САПР при построении чертежей и изображений машиностроительных изделий и их деталей.
Центральное проецирование применяется при синтезе изображений пространственных сцен большой протяженности. В этом виде проецирования учитывается то, что в реальном мире видимые размеры объектов уменьшаются при удалении от наблюдателя пропорционально расстоянию (рис. 4. 10).
Центральное проецирование состоит из двух преобразований – перспективного преобразования и преобразования ортогонального проецирования. На рис. 4.10 показаны результат перспективного преобразования параллелепипеда с точкой P¢ и последующее ортогональное проецирование его на плоскость OXY.
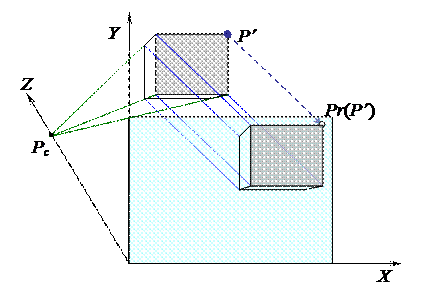
Рис. 4.10
Перспективное преобразование приводит к фактическому сокращению размеров объектов с удалением их от наблюдателя. В однородных координатах перспективное преобразование с осью проецирования OZ представляется следующим образом:
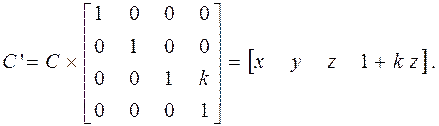 (4.32)
(4.32)
Коэффициент k называется коэффициентом перспективы. Он определяет степень сокращения видимых размеров в зависимости от удаления. Геометрически коэффициент k определяет положение точки схода Pc на оси OZ, в которой в результате преобразования сходятся все линии, располагавшиеся параллельно оси OZ.
В данном случае перевод однородных координат в обычные требует деления на значение координаты v. В итоге обычными координатами точки P' будут (x /(k z + 1), y /(k z + 1), z /(k z + 1)).
Чтобы определить координаты точки схода, вычислим пределы:
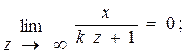 (4.33)
(4.33)
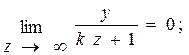 (4.34)
(4.34)
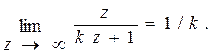 (4.35)
(4.35)
Таким образом, для преобразования (4.32) Pc = (0, 0, 1/ k). Если требуется построить центральную проекцию с точкой схода, координаты xc и yc которой отличны от нуля (например должны соответствовать центру области вывода), то используют тот же прием, что и при выполнении геометрических преобразований относительно заданного центра. В данном случае сначала необходимо выполнить преобразование смещения по x и y на - xc и - yc соответственно, затем перспективное преобразование, а в заключение – обратное преобразование смещения.
Преобразование ортогонального проецирования после перспективного необходимо для получения проекций объектов на картинную плоскость.
Поскольку перспективное преобразование искажает размеры и ориентацию в пространстве элементов поверхностей, то для правильного моделирования распространения света фотометрические расчеты следует производить до перспективного преобразования, а удаление невидимых точек поверхностей должно выполняться после перспективного преобразования. На практике это может значительно усложнить расчеты, поэтому чтобы не исказить фотометрические расчеты, часто перспективное преобразование применяют и к источникам освещения. Такой прием позволяет совместить удаление невидимых точек и фотометриеские расчеты в одном этапе обработки.
Более подробный материал по видам проецирования и их свойствам можно найти в [4, 7].
4.9. Ориентация и потенциальная видимость
поверхностей
Обычно поверхности служат границами геометрических тел, поэтому при машинном формировании изображения геометрическго тела необходимо различать между собой внутреннюю, т.е. обращенную в сторону внутренних точек тела, и внешнюю стороны его поверхности. Это важно при визуализации, поскольку на изображении должны быть видимы только внешние стороны поверхностей.
Формально стороны поверхности можно различать по направлению нормального вектора к ней. Для определенности примем правило, согласно которому внешней стороной поверхности геометрического тела будет считаться та, со стороны которой располагаются нормальные векторы к поверхности, рассчитанные аналитически. Выше уже говорилось, что для поверхности с уравнением F (x, y, z) = 0 нормальный вектор в любой ее точке находится как 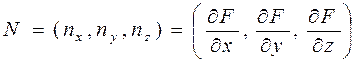 .
.
Чтобы лучше понять важность принятого правила, рассмотрим следующий пример. Пусть задана сферическая поверхность с уравнением x 2 + y 2 + z 2 – R 2 = 0 (рис. 4.11). Из уравнения следует, что нормальный вектор к этой п
 2014-02-12
2014-02-12 895
895






