Многомерные массивы
Многомерные массивы отличаются от одномерных только тем, что каждый элемент характеризуется не одним, а двумя или более индексами. Они используются, например, для хранения таблиц (каждый элемент таблицы имеет 2 индекса - № строки и № столбца).
Декларация многомерного массива имеет следующий формат:
тип ID [ размер 1] [ размер 2]…[ размерN ] =
{ { список начальных значений },
{ список начальных значений },
…
};
Списки начальных значений – атрибут необязательный.
Пример:
int a[3][3]={ {1,2,3}, {4,5,6}, {7,8,9} };
Аналогично, при обращении к конкретному элементу многомерного массива указывается имя массива и затем - последовательно индексы элемента, каждый в квадратных скобках; например:
a[2][1]
a[i+1][k]
Рассмотрим особенности работы с многомерными массивами на конкретном примере двумерного массива (двумерные массивы называют также матрицами):
#include <stdio.h>
void main()
{
int i, j;
int m[3][4] = { { 1, 2, 3, 4}, {11,12,13,14}, {21,22,23,24} };
for (i=0; i<3; i++) {
printf("\n %2d)", i+1);
for (j=0; j<4; j++)
printf(" %3d",m[ i ] [ j ]);
}
}
Результаты работы программы:
1) 1 2 3 4
2) 11 12 13 14
3) 21 22 23 24
а) Простейшие примеры
Задача 1. Ввести матрицу и увеличить все ее элементы на единицу.
#include<iostream.h>
#include<conio.h>
#include<stdio.h>
void main() {
int a[10][10],n,m,i,j;
// Ввод матрицы
cout<<"Vvedite n,m <=10:";
cin>>n>>m;
cout<<"Vvedite massiv:\n";
for (i=0; i<n; i++)
for (j=0; j<m; j++)
cin>>a[i][j];
// Увеличение на 1
for (i=0; i<n; i++)
for (j=0; j<m; j++)
a[i][j]++;
// Вывод матрицы
puts("Result:");
for (i=0; i<n; i++)
for (j=0; j<m; j++)
printf("%3d%c", a[i][j], j==m-1? '\n': ' ');
getch();
}
Задача 2. Найти в матрице наибольший элемент и его позицию.
max=a[0][0];
im=jm=0;
for (i=0; i<n; i++)
for (j=0; j<m; j++)
if (a[i][j]>max) {
max=a[i][j];
im=i;
jm=j;
}
printf("Max element a[%d][%d]=%d\n", im, jm, max);
Задача 3. Переписать матрицу в одномерный массив.
int b[100];
for (i=k=0; i<n; i++)
for (j=0; j<m; j++)
b[k++]=a[i][j];
После выполнения этого участка программы k=n*m -количество элементов в полученном массиве.
б) Диагонали квадратной матрицы
Квадратной называется матрица, у которой число строк равно числу столбцов. Ее главной диагональю называется диагональный ряд элементов, идущий из верхнего левого угла в нижний правый, а побочной диагональю - идущий из верхнего правого угла в нижний левый:
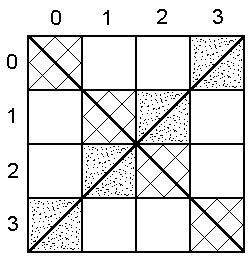
Обозначим размер матрицы буквой N, индекс строки буквой I, а индекс столбца буквой J. Тогда у элементов, лежащих на главной диагонали, I = J, а у элементов, лежащих на побочной диагонали, I + J = N - 1.
Задача 4. Найти сумму элементов матрицы, лежащих над главной диагональю.
Из рисунка видно, что у элементов, лежащих над главной диагональю,
I < J.
Можно учесть это в условии оператора if, либо цикла for:
for (i=s=0; i<n; i++)
for (j=i+1; j<n; j++)
s+=a[i][j];
в) Работа со строками и столбцами
Строка или столбец матрицы аналогичны одномерному массиву. Поэтому к ним применимы все алгоритмы, рассмотренные для одномерных массивов.
В применении же ко всей матрице это обычно требует дополнительного внешнего цикла (циклов).
Задача 5. Поменять местами первую и последнюю строки матрицы.
for (j=0; j<m; j++) {
p=a[0][j];
a[0][j]=a[n-1][j];
a[n-1][j]=p;
}
Задача 6. Найти сумму элементов в каждой строке матрицы.
Поскольку строк в матрице несколько, ответом будет не одно число, а одномерный массив:
int b[10];
for (i=0; i<n; i++) {
for (j=s=0; j<m; j++)
s+=a[i][j];
b[i]=s;
}
for(i=0; i<n; i++)
printf("%d ", b[i]);
puts("");
Задача 7. Найти сумму элементов в каждом столбце матрицы.
По сравнению с предыдущей задачей, здесь изменится порядок циклов (ведь сначала нужно целиком подсчитать сумму в одном столбце, и только затем - в другом и т.д.):
for (j=0; j<m; j++) {
for (i=s=0; i<n; i++)
s+=a[i][j];
b[j]=s;
}
for(j=0; j<m; j++)
printf("%d ", b[j]);
puts("");
Задача 8. В каждой строке матрицы определить количество элементов, равных нулю. Отсортировать строки матрицы по убыванию этого количества.
Прежде всего, нужно определить эти количества и занести их в одномерный массив (обозначим его b):
for (i=0; i<n; i++) {
for (j=s=0; j<m; j++)
if (a[i][j]==0) s++;
b[i]=s;
}
Затем нужно отсортировать матрицу. В процессе этого обменивать местами нужно как сами строки, так и соответствующие им элементы одномерного массива b (чтобы каждый его элемент продолжал соответствовать своей строке):
for (i=0; i<n; i++)
for (k=i+1; k<n; k++)
if (b[k]>b[i]) {
for(j=0; j<m; j++)
{ p=a[i][j]; a[i][j]=a[k][j]; a[k][j]=p; }
p=b[i]; b[i]=b[k]; b[k]=p;
}
 2014-02-12
2014-02-12 385
385






