Испытание статистических гипотез

· Проверка гипотез – вторая задача математической статистики

· Гипотеза о соответствии кривой статистическому материалу

· Понятие о критерии согласия – о том, что отклонения вызваны чисто случайными причинами

· Гипотеза о теоретическом распределении

· Критерий согласия – величина 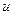, определяемая по отклонениям гистограммы от предполагаемой кривой распределения. Чем меньше эти отклонения, тем более гистограмма соответствует предполагаемому закону распределения.

· Величина критерия 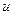может быть определена по-разному. Обычно критерий согласия 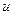выбирается так, чтобы он увеличивался с увеличением расхождения между гистограммой и сравниваемой с ней кривой плотности вероятности

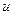· - случайная величина и имеет распределение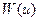

· Определенный по выборке критерий должен находиться вблизи середины распределения. Если гистограмма не соответствует предполагаемому закону распределения, то критерий 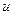сдвигается вправо

Правило применения критерия согласия:

Если вероятность 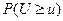мала, например, меньше 0,1 или 0,01, то гипотеза отвергается. Эта граничная величина (0,1 или 0,01) называется уровнем значимости. Чем строже требования к соответствию выборки предполагаемому закону распределения, тем больше выбирается уровень значимости.

Критерий Пирсона .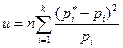

Здесь 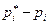- отклонение частоты в i -м разряде гистограммы (всего k разрядов) от теоретической вероятности 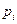попадания в i -й разряд; n – объем выборки.

К.Пирсон показал, что распределение u есть распределение суммы квадратов r нормально распределенных случайных величин (т.н. хи-квадрат распределение с r степенями свободы).

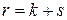, где s – число независимых связей, налагаемых на 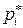при определении 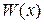: условие нормировки + число независимых моментов (параметров распределения). Например, для нормального распределения .

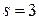При большом n распределение хи-квадрат практически не зависит от .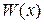

Величина 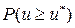для хи-квадрат распределения табулирована.

· Далее при помощи специальных таблиц определяется 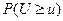и сравнивается с некоторой заранее выбранной величиной, называемой уровнем значимости. Если 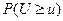меньше этой величины, гипотеза о соответствии отвергается.

Критерий Колмогорова 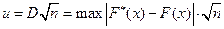, здесь 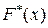- статистическая, и 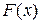- теоретическая функции распределения, n – объем выборки.