| Средства ИКТ | Компьютер. |
| Колонки. | |
| Мультимедийный проектор. | |
| Интерактивная доска. | |
| Принтер. | |
| Сканер. | |
| Цифровые образовательные ресурсы | Электронные учебники и тренажёры, в том числе занимательные задания по предмету. |
| Электронные хрестоматии и энциклопедии. | |
| Коллекция цифровых образовательных ресурсов. | |
| Перечень Интернет-сайтов. | |
| Интерактивные наглядные пособия. | |
| Учебно-методическая литература | Методическая литература для учителя. |
| Учебно-методические комплекты для учащихся автора Моро. | |
| Хрестоматии. | |
| Энциклопедии. | |
| Словари. | |
| Справочные пособия. | |
| Периодические издания по предмету. | |
| Учебно-практическое и лабораторное оборудование | Комплекты для счёта и действий с числами. |
| Модели математических фигур и тел. | |
| Приборы для измерения массы, длины, площади, скорости и объёма, времени. | |
| Инструменты для конструирования геометрических фигур. | |
| Латинский алфавит. | |
| Калькуляторы. | |
| Счёты. | |
| Экранно-звуковые средства | Аудиозаписи в соответствии с программой обучения. |
| CD-диски с фильмами и мультфильмами, соответствующими тематике учебного курса. | |
| Слайды (мультимедийные презентации), соответствующие тематике учебного курса. |
Матричный метод решения систем линейных алгебраических уравнений
|
|
|
С помощью теории матриц любую систему линейных алгебраических уравнений можно представить и решить в простой и наглядной форме.
Пусть задана система уравнений общего вида. Неизвестные 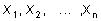 и свободные члены
и свободные члены 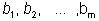 представим как векторы - столбцы
представим как векторы - столбцы
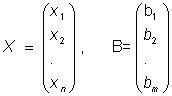 .
.
Коэффициенты 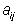 при неизвестных запишем в виде матрицы порядка
при неизвестных запишем в виде матрицы порядка 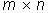
 .
.
Тогда система может быть записана в виде одного матричного уравнения
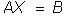 (1)
(1)
относительно неизвестной матрицы - столбца X.
Под решением матричного уравнения (1) понимают такую матрицу - столбец X, которая обращает данное уравнение в верное равенство. Это возможно не для всякой матрицы A, а только для квадратной и невырожденной.
Итак, пусть A - матрица коэффициентов системы квадратная 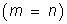 и невырожденная. В таком случае существует обратная матрица
и невырожденная. В таком случае существует обратная матрица 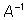 . Очевидно, что
. Очевидно, что 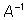 согласована с матрицами
согласована с матрицами 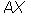 и B.
и B.
Умножив обе части матричного уравнения (1) слева на матрицу 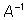 , получим
, получим
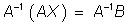 .
.
Отсюда с учетом свойств умножения матриц, следует
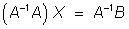 .
.
Так как 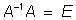 , а
, а 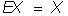 , то
, то
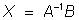 . (2)
. (2)
Вектор - столбец неизвестных X определяется однозначно. Убедимся, что этот вектор удовлетворяет уравнению (1). Подставив соотношение (2) в уравнение (1), получим
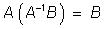 , откуда
, откуда 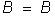 .
.
Итак, матрица - столбец (2) удовлетворяет уравнению (1), следовательно, является его единственным решением.
Пример. Решить матричным методом систему линейных уравнений
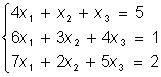 .
.
Решение. Запишем систему в виде матричного уравнения
|
|
|
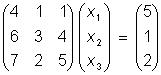 .
.
Найдем обратную матрицу 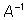
 .
.
По формуле (2) находим решение системы
 .
.
Таким образом, 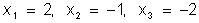
 2014-10-30
2014-10-30 384
384






