6.1. Базові булеві функції
6.2. Аксіоми і закони булевої алгебри
6.1. Базові булеві функції
Як вже зазначалося, інформація всередині ЕОМ представляється у вигляді сукупності біт, тобто в двійковій формі. Для синтезу схем, обробних двійкову інформацію, використовується спеціальний математичний апарат, званий булевою алгеброю. Елементами булевої алгебри є булеві константи, булеві застосування і булеві операції. Існують дві булеві константи, які прийнято позначати 0 і I. Ці константи не розглядаються як числа і для їх позначення можна використовувати будь-які слова (наприклад, так і ні. Істина і брехня, true і false і т.д.). Булеві змінні можуть приймати лише значення булевих констант, тобто 0 або 1. Таким чином, змінна х l називається булевої змінною, якщо і тільки якщо 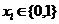 .
.
Булева алгебра включає три операції, а саме: заперечення (- кон'юнкцію і диз’юнкцію. Ці операції представлені в табл. 6.1 для булевих змінних а і b.
Таблиця 6.1
Операції булевої алгебри
| а | b | Заперечення а | Заперечення b | а˄b | a˅b |
Часто заперечення називається операцією «НЕ» і вираз ̚ a читається як «НЕ a». Для стислості це позначається як 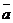 . Операція ˄ часто називається логічним множенням, а також операцією «І». При цьому «а І b» позначається як а & Ь, а * b або аb. Операція ˅ часто називається логічним складанням, а також операцією «АБО». При цьому «а або b» позначається як а+b. Очевидно, кон'юнкція довільного числа булевих змінних дорівнює одиниці, якщо і тільки якщо всі ці змінні дорівнюють одиниці. Аналогічно, диз'юнкція довільного числа булевих змінних дорівнює нулю, якщо і тільки якщо всі ці змінні дорівнюють нулю. Тому кон'юнкцію (диз'юнкцію) іноді називають операцією вибору мінімального (максимального) значення змінних.
. Операція ˄ часто називається логічним множенням, а також операцією «І». При цьому «а І b» позначається як а & Ь, а * b або аb. Операція ˅ часто називається логічним складанням, а також операцією «АБО». При цьому «а або b» позначається як а+b. Очевидно, кон'юнкція довільного числа булевих змінних дорівнює одиниці, якщо і тільки якщо всі ці змінні дорівнюють одиниці. Аналогічно, диз'юнкція довільного числа булевих змінних дорівнює нулю, якщо і тільки якщо всі ці змінні дорівнюють нулю. Тому кон'юнкцію (диз'юнкцію) іноді називають операцією вибору мінімального (максимального) значення змінних.
Булеву формулу можна визначити наступним чином:
- кожна булева змінна і константа є формулою;
- якщо А і В - формули, то формулами є виразами ̚ А, ̚ В, А ˄ В, А ˄ В;
- інших формул не існує.
Булеві формули визначають особливий клас функцій, а саме булевих. Для завдання порядку виконання операцій у формулі використовуються дужки. Якщо дужок нема, то першою виконується операція ̚, потім ˄ і в останню чергу – операція ˄. Відзначимо, що булева функція приймає тільки одне з двох фіксованих значень. Нехай функція f(х) залежить від L булевих змінних від x1 до xL. З цих змінних можна утворити послідовність двійкових векторів, відповідних десятковим числах від 0 до 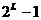 . Таким чином, існує
. Таким чином, існує
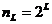 (6.1)
(6.1)
різних наборів L булевих змінних. На кожному з цих наборів функція може приймати тільки одне з двох значень. Отже, існує
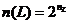 (6.2)
(6.2)
різних булевих функцій L булевих змінних. Це число швидко зростає зі зростанням L. Так, при L= 0 маємо n(0) = 2, при L =1 маємо n(1)= - 2, L=2 дає n(2) = 16, а при L=5 маємо nL=- 32 і існує 4.294967296 різних булевих функцій. У табл. 6.2 наведені всі шістнадцять булевих функцій для двох змінних, тобто для
L=2.
Таблиця 6.2
Булеві функції двох змінних
| а | b | 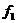
| 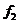
| 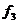
| 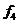
| 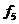
| 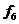
| 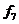
| 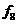
| 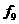
| 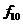
| 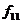
| 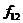
| 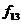
| 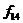
| 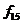
| 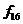
|
Розглянемо функції з табл. 6.2, що мають практичне значення для синтезу схем блоків:
1. Функції 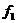 і
і 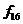 є відповідно константами 0 і 1. Ці функції не залежать від значень змінних а і b, тобто ці змінні є несуттєвими для функцій
є відповідно константами 0 і 1. Ці функції не залежать від значень змінних а і b, тобто ці змінні є несуттєвими для функцій 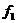 і
і 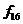 .
.
2. Функція 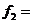 a ˄ b = а & Ь = а • Ь = аb, тобто це кон'юнкція а і Ь. Цю функцію можна записати і для довільного числа змінних
a ˄ b = а & Ь = а • Ь = аb, тобто це кон'юнкція а і Ь. Цю функцію можна записати і для довільного числа змінних 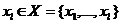 в наступному вигляді:
в наступному вигляді:
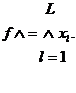
3. Функція 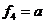 «і функція
«і функція 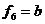 . Ці функції повторюють значення відповідних змінних. При цьому функція
. Ці функції повторюють значення відповідних змінних. При цьому функція 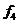 має b, а функція
має b, а функція 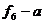 .
.
4. Функція 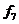 , що дорівнює одиниці при розбіжності значень а і b. Ця функція називається «нерівнозначність», «виключає або» або «сума по модулю 2». Для позначення цієї операції використовується знак
, що дорівнює одиниці при розбіжності значень а і b. Ця функція називається «нерівнозначність», «виключає або» або «сума по модулю 2». Для позначення цієї операції використовується знак  , тобто
, тобто 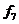 = а
= а  b. При довільному числі змінних ця функція дорівнює одиниці, якщо число одиниць в наборі вхідних змінних непарній. Іноді ця функція називається функцією перевірки на парність.
b. При довільному числі змінних ця функція дорівнює одиниці, якщо число одиниць в наборі вхідних змінних непарній. Іноді ця функція називається функцією перевірки на парність.
5. Функція 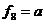 ˅ b = a + b, тобто це диз'юнкція а і b. Цю функцію можна записати у вигляді
˅ b = a + b, тобто це диз'юнкція а і b. Цю функцію можна записати у вигляді
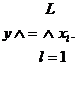
для довільного числа змінних.
6. Функція 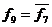 , називається «запереченням диз'юнкції» або «АБО-НЕ». Цю функцію можна записати, використовуючи знаки v і
, називається «запереченням диз'юнкції» або «АБО-НЕ». Цю функцію можна записати, використовуючи знаки v і 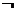 у вигляді
у вигляді 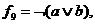 або знаки + і
або знаки + і 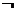 тобто
тобто 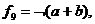 крім того (найбільш часто) використовується запис
крім того (найбільш часто) використовується запис 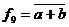 або
або 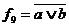 . Іноді називається стрілкою Пірса і позначається як
. Іноді називається стрілкою Пірса і позначається як 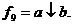 .
.
7. Функція 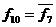 називається «рівнозначність» або тотожність. Ця функція дорівнює одиниці при рівності всіх змінних вхідного набору.
називається «рівнозначність» або тотожність. Ця функція дорівнює одиниці при рівності всіх змінних вхідного набору.
8. Функція 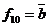 і
і 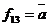 . Відзначимо, що для функції
. Відзначимо, що для функції 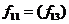 змінна а (b) є несуттєвою.
змінна а (b) є несуттєвою.
9. Функція 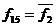 , звана «запереченням кон'юнкції» або функція «І-НЕ». Ця функція записується в одній з наступних форм
, звана «запереченням кон'юнкції» або функція «І-НЕ». Ця функція записується в одній з наступних форм 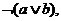
 (a & b),
(a & b),  (a*b),
(a*b), 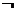 (ab),
(ab), 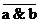 ,
, 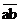 . Іноді ця функція називається штрих Шиффера і позначається у вигляді
. Іноді ця функція називається штрих Шиффера і позначається у вигляді 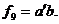
В англомовній нотації заперечення називається функцією NOT, кон'юнкція - AND, диз'юнкція - OR, заперечення кон'юнкції - NAND, заперечення диз'юнкції - NOR і нерівнозначність - EXOR.
10) Функція 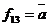 і
і 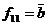 . Ці функції заперечують значення відповідних змінних.
. Ці функції заперечують значення відповідних змінних.
Як видно з табл. 6.2, функції двох змінних включають константи (0, 1), чотири функції однієї змінної (a, b, 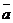 ,
, 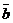 ) і десять функцій двох змінних. Аналогічно можна побудувати таблиці, що задають функції довільного числа булевих змінних. Однак у цьому немає необхідності, тому що значення функцій, що залежать від будь-якого числа змінних, можна визначити, знаючи спосіб обчислення функцій з табл. 6.2.
) і десять функцій двох змінних. Аналогічно можна побудувати таблиці, що задають функції довільного числа булевих змінних. Однак у цьому немає необхідності, тому що значення функцій, що залежать від будь-якого числа змінних, можна визначити, знаючи спосіб обчислення функцій з табл. 6.2.
Наприклад, знайдемо значення функції 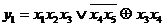 на наборі
на наборі 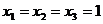 ,
, 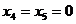 . Використовуємо для цього функції двох змінних. Введемо наступні позначення:
. Використовуємо для цього функції двох змінних. Введемо наступні позначення: 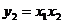 ,
, 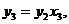
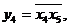
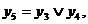
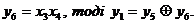 Використовуючи табл. 6.2, знайдемо
Використовуючи табл. 6.2, знайдемо 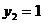 ,
, 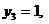
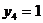 ,
, 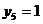 ,
, 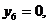
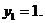
Схеми ЕОМ будуються з логічних елементів, званих вентилями. При цьому практичне значення мають тільки вентилі, що відповідають повноваженням NOT, NAND і NOR. Це пов'язано з тим, що вентилі будуються на основі транзисторів, які мають внутрішню інверсію. Тому вентиль, відповідний функції NAND (NOR) має менше транзисторів і змінює свій стан в два рази швидше, ніж вентиль AND (OR). Вентилі, що відповідають повноваженням AND і OR, мають теоретичне значення, як і вентиль, відповідний функції EXOR. Позначення основних вентилів для європейського і американського стандартів показані в табл. 6.3.
Таблиця 6.3
Позначення основних вентилів
Далі в цій книзі ми будемо використовувати європейські позначення вентилів. Відзначимо, що вентилі можуть мати довільне число входів, як правило, воно обмежено на практиці числом 8. Природно, вентиль NОТ має тільки один вхід. При цьому вентиль NOT будемо називати «інвертор», вентиль AND - «кон'юнктор», вентиль OR - «диз'юнктор».
6.2. Аксіоми і закони булевої алгебри
Як і звичайна алгебра, булева алгебра містить ряд фундаментальних правил, які приймаються без доказів і називаються аксіомами. Аксіоми служать основою для доказу теорем, що є законами булевої алгебри. Аксіоми і закони використовуються для спрощення булевих функцій, що дозволяє побудувати схеми з певними характеристиками, звичайно з мінімальним числом-елементів.
Розглянемо аксіоми булевої алгебри, звані іноді постулатами.
1. Булева мінлива х завжди дорівнює або нулю, або одиниці:
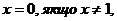 (А1)
(А1)
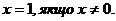 (А2)
(А2)
Тут 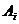 означає аксіоми, які пронумеровані для подальшого використання.
означає аксіоми, які пронумеровані для подальшого використання.
2. Інверсне значення змінної х протилежно її прямим значенням:
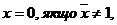 (А3)
(А3)
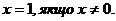 (А4)
(А4)
3. Логічне множення підпорядковується наступним правилам:
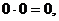 (А5)
(А5)
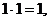 (А6)
(А6)
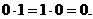 (А7)
(А7)
4. Логічне додавання підпорядковується наступним правилам:
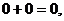 (А8)
(А8)
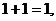 (А9)
(А9)
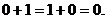 (А10)
(А10)
Отримана система аксіом, прямо випливає з визначених функцій НЕ, І і АБО, є основою для доказу теорем булевої алгебри. Оскільки нас цікавлять прикладні аспекти булевої алгебри, то ми розглянемо тільки теореми для функцій НЕ, І, АБО, які утворюють логічний базис. Розглянемо основні теореми 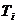 і їх докази.
і їх докази.
1. Ідентичність.
х + 0 = х, (Т1)
х*1= х. (Т2)
Доказ теореми 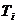 випливає з аксіом А8 і А10, в яких перший доданок замінено на х. Теорема Т1 говорить, що з булева висловлювання можна видалити частину, рівну нулю і пов'язану з рештою виразом операцією диз'юнкція. Теорема Т2 доводиться на основі аксіом А6 і А7 і каже, що з булева висловлювання можна видалити частину, рівну одиниці і пов'язану з рештою виразом операцією кон'юнкція.
випливає з аксіом А8 і А10, в яких перший доданок замінено на х. Теорема Т1 говорить, що з булева висловлювання можна видалити частину, рівну нулю і пов'язану з рештою виразом операцією диз'юнкція. Теорема Т2 доводиться на основі аксіом А6 і А7 і каже, що з булева висловлювання можна видалити частину, рівну одиниці і пов'язану з рештою виразом операцією кон'юнкція.
2. Наявність нульових елементів.
х +1 = 1, (Т3)
х*0 = 0. (Т4)
Теорема Т3, випливає з аксіом А9 і А10 про те, що якщо якась булева часина висловлювання, пов'язана з рештою виразом операцією диз'юнкція, дорівнює одиниці, то і всі вираз дорівнює одиниці. Теорема Т4 випливає з аксіом А5, і А6, які свідчать про те, що якщо якась частина булева висловлювання, пов'язана з рештою виразом знаком кон'юнкція, дорівнює нулю, то всі вираз дорівнює нулю.
3. Ідемпотентність.
х + х = х, (Т5)
х * х = х. (Т6)
Теорема Т5 випливає з аксіом А5 і А9. Вона свідчить, що додавання або видалення ідентичних частин булева висловлювання, пов'язаних операцією диз'юнкція з іншою частиною вислови, не змінює значення булева висловлювання. Теорема Т5 може бути доведена за індукції в наступному вигляді:
х+х+... +х = n*х = х.
Теорема Т6 випливає з аксіом А5 і А6 вона свідчить про те, що при множенні булевого висловлювання на самого себе не змінює значення булева висловлювання. Теорема Т6 може бути розширена до х*х ***х= 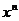 = х.
= х.
4. Еволюція (подвійне заперечення).
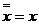 (Т7)
(Т7)
Теорема Т7 доводиться послідовним застосуванням аксіом А3 і А4 або з використанням методу повної індукції. Ідея методу полягає в побудові таблиці істинності для лівої і правої частин доказуваного рівності. Якщо на всіх наборах вхідних змінних значення лівої і правої частин збігаються, то вони ідентичні і, отже, теорема доведена. Для доказу Ту побудуємо табл. 6.4.
Таблиця 6.4
| х | 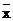
| 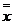
|
Як видно з табл. 6.4, значення х і 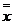 - збігаються для всіх вхідних наборів. Отже, теорема Т7 справедлива.
- збігаються для всіх вхідних наборів. Отже, теорема Т7 справедлива.
З Т7 слідує, що подвійне заперечення булевого висловлювання не змінює його значення. Таким чином, будь-яке парне число заперечень булева висловлювання може бути введене або видалено без зміни його значення.
5. Доповнюваність.
х+ 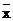 =1, (Т8)
=1, (Т8)
х* 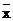 = 0. (Т9)
= 0. (Т9)
Доказ цих теорем наведено в табл. 6.5
Таблиця 6.5
| x | 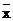
| x+ 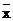
| x* 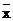
|
Теореми T7 і Т9 часто використовуються для доказу інших теорем, а також для спрощення булевих виразів.
6. Асоціативність.
(a+b)+c = а+b (b+c), (T10)
(ab)c = а(bc). (T11)
Теореми T10 і T11 повністю аналогічні теоремам звичайної алгебри. Вони свідчать, що значення булева висловлювання не залежить від порядку обчислення значень його частин.
7. Комутативність.
а + b = b + а, (T12)
а*b = b*а. (T13)
Теореми T12 і T13 свідчать про те, що перестановка членів булева висловлювання не змінює його значення. Ці теореми аналогічні теоремам звичайної алгебри.
8. Дистрибутивність
ab+ас = а(b+с), (T14)
(a+b) (а+с) = а+bс. (T15)
Теорема Т14 має свого аналога в звичайній алгебрі, а теорема T15 вимагає докази. Проведемо доказ шляхом перетворення лівої частини T15. Якщо в результаті перетворень з лівої частини вийде права частина, то теорема доведена.
Доведення:
(a+b)(a +с) = а*а+b*а+а*c+b*c [Т14] = а+а*b+a*c+b*c[Т6, Т13] =
= a*1+a*b+a*c+b*c[Т2]=a(1+b+c)+bc[T14] = а*1+b*c[Т3] =а+b*c[Т2]
Отже, (а + b) (а + с) = а + bс.
Після кожного перетворення виразів у квадратних дужках наведені теореми, на підставі котрих проведенні ці перетворення.
9. Поглинання.
а + аb = а, (Т16)
а (а + b) = а (T17)
Теореми T16 I T17 дозволяють зменшити число членів булевого висловлювання. Доведемо, наприклад, теорему T16:
а + аb = a*1+аb*[Т2] = а (1 + b) * [Т14] = а*1 [Т2] = а.
Для доказу теореми T17 зведемо її до T16:
а (а +b) = а*а + а*b[Т14]=а+а*b= a[T16].
10. Склеювання.
ab+a 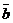 = a, (T18)
= a, (T18)
(a+b) (а+ 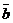 ) = а. (Т19)
) = а. (Т19)
Теореми T18 і T19 також дозволяють зменшити число членів булевого висловлювання. Доведемо, наприклад, теорему Т18:
ab+a 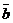 =a(b+
=a(b+ 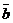 )[T14]=а*[T8]=a[Т2].
)[T14]=а*[T8]=a[Т2].
Тепер доведемо теорему T19:
(a+b) (a+ 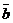 ) = аа+a
) = аа+a 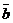 +ba+b
+ba+b 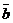 [T14]=а+a
[T14]=а+a 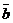 +ab+0[T6, T13,T9]=a+a[T18,T1]=a[T5].
+ab+0[T6, T13,T9]=a+a[T18,T1]=a[T5].
11. Теореми Де Моргана.
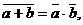 (T20)
(T20)
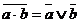 . (T21)
. (T21)
Теореми Де Моргана мають найважливіше значення при синтезі комбінаційних схем. Теорема T20 читається як "заперечення диз'юнкції еквівалентно кон'юнкції заперечень ". Доведемо теорему Т20, для чого скористаємося наступною лемою.
Лема. Якщо для булевих змінних А і В одночасно виконуються умови АВ = 0 і А  В=1, то А =
В=1, то А = 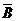 .
.
Для доказу леми розглянемо табл. 6.6, з якої випливає, що умови АВ = 0 і А  В = 1 виконуються одночасно для наборів А= 0, В=1 і А=1, В=0. Таким чином, А=
В = 1 виконуються одночасно для наборів А= 0, В=1 і А=1, В=0. Таким чином, А= 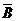 .
.
Таблиця 6.6
| А | В | АВ | А  В В
|
Доказ теореми Т20. Позначимо А=a+b і В= 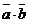 . Знайдемо значення виразів АВ і А
. Знайдемо значення виразів АВ і А  В. Якщо ми отримаємо AB=0 і А
В. Якщо ми отримаємо AB=0 і А  B =1, то з доведеної леми буде слідувати, що А=
B =1, то з доведеної леми буде слідувати, що А= 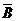 .
.
АВ = (а+b) (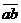 ) = а
) = а 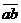 +b
+b 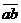 [Т14]=0+0[T9]=0[Т8].
[Т14]=0+0[T9]=0[Т8].
А  B = а + b +
B = а + b + 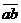 =a(b
=a(b 
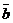 )+b(a
)+b(a 
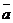 )[T8,T2]+
)[T8,T2]+ 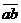 =ab
=ab  a
a 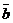

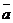 b[Т14,Т13]
b[Т14,Т13] 

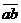 =ab
=ab  a
a 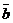

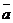 b
b 
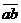 [T5]=(ab
[T5]=(ab  a
a 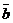 )
)  (
(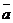 b
b 
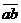 )[T14]=a
)[T14]=a 
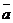 [T18]=1[T8]
[T18]=1[T8]
Tак, обидві умови леми справедливі, отже, маємо А = 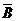 і
і 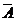 =B то є а+b=
=B то є а+b= 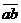 .
.
Теорема доводиться аналогічно аналітичним шляхом, проте доведемо її методом повної індукції (Табл. 6.7). З таблиці. 6.7 випливає, що значення в стовпцях аb і 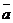

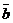 збігаються для всіх вхідних наборів, отже, теорема Т21 справедлива. Теорема Т21 читається так: "заперечення кон'юнкції еквівалентне диз'юнкції заперечень".
збігаються для всіх вхідних наборів, отже, теорема Т21 справедлива. Теорема Т21 читається так: "заперечення кон'юнкції еквівалентне диз'юнкції заперечень".
Таблиця 6.7
| a | b | ab | 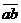
| 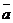
| 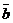
| 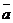  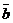
|
Теореми T20 і T21 справедливі для будь-якого числа вхідних змінних і можуть бути записані в наступному вигляді:
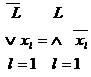 ; (6.2)
; (6.2)
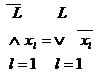 ; (6.2)
; (6.2)
У табл. 6.8 наведені основні теореми булевої алгебри разом з їх російськими та англійськими назвами.
Число теорем булевої алгебри набагато більше, але для синтезу логічних схем цілком достатньо знання теорем Т1 –Т21.
Таблиця 6.8
Основні теореми булевої алгебри
| № | Теорема | Назва | ||
| Т1 Т2 | x+0=x, x*1=x. | Ідентичність Identities | ||
| Т3 | x +1=1, | Наличие нулевых элементов | ||
| T4 | X*0=0 | Null elements | ||
| T5 T6 | x+x=x x*x=x | Ідемпотентний Idempotency | ||
| T7 | 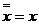
| Еволюціний; Involution | ||
| T8 T9 | 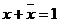
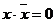
| Доповняльний Complements | ||
| T10 T11 | (a+b)+c=a+(b+c), (ab)c=a(bc) | Асоцыативний Associative | ||
| T12 T13 | a+b=b+a, a*b=b*a | Комутативний Commutative | ||
| T14 T15 | ab+ac=a(b+c) (a+b)(a+c)=a+bc | Дистрибутивний Distributive | ||
| T16 T17 | a+ab=a a+(a+b)=a | Поглинання Absorption | ||
| T18 T19 | ab+ 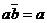 (a+b)(a+
(a+b)(a+ 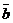 )=a )=a
| Склеювання Expansion | ||
| T20 T21 | 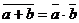
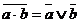
| Теореми Де Моргана De Morgan's theorems | ||
 2015-01-30
2015-01-30 525
525






