Умножив правые и левые части формул (25) на lН, получим проекции суммарной напряженности магнитного поля судна и поля Земли на направление магнитного меридиана и на перпендикулярное ему направление:
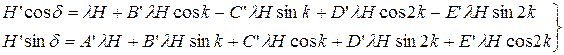 | (28) |
Входящие в это выражения 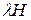 , A’
, A’ 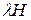 , B’
, B’ 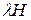 , C’
, C’ 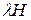 , D’
, D’ 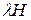 , E’
, E’ 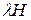 называются судовыми магнитными силами, хотя на самом деле это напряженности, но будем называть их силами.
называются судовыми магнитными силами, хотя на самом деле это напряженности, но будем называть их силами.
Как мы знаем, для перехода к силе взаимодействия нужно напряженность поля умножить на магнитный заряд, который взаимодействует с данным полем. В выражениях судовых магнитных сил напряженность умножают не на заряд а на отвлеченные числа.
Рассмотрим судовые магнитные силы. Все силы кроме B’ 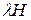 , C’
, C’ 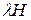 вызваны действием мягкого судового железа. Силы же B’
вызваны действием мягкого судового железа. Силы же B’ 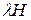 , C’
, C’ 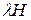 вызваны действием жесткого железа, и лишь отчасти в них проявляется мягкое. Рассмотрим силы подробно.
вызваны действием жесткого железа, и лишь отчасти в них проявляется мягкое. Рассмотрим силы подробно.
lH. Примем в уравнениях (28) все коэффициенты равными нулю. Тогда выражения примут следующий вид:
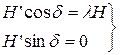
Так как H’ не может быть равной нулю, значит, девиация равна нулю. Таким образом, сила 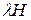 совпадает с направлением магнитного меридиана и девиации не производит. Значит сила
совпадает с направлением магнитного меридиана и девиации не производит. Значит сила 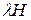 является полезной силой, и нужно стремиться к ее увеличению. Достичь этого можно увеличивая коэффициент l путем установки брусков мягкого железа около компаса, что практически не выполняется из-за громоздкости и дороговизны таких брусков. На современных судах коэффициент l в районе установки магнитного компаса равен 0,8 – 0,9. Если l меньше 0,3 то компас плохо работает даже в средних магнитных широтах. Хотя сила lН сама девиации не производит, но косвенно влияет на ее величину. В выражениях (24)
является полезной силой, и нужно стремиться к ее увеличению. Достичь этого можно увеличивая коэффициент l путем установки брусков мягкого железа около компаса, что практически не выполняется из-за громоздкости и дороговизны таких брусков. На современных судах коэффициент l в районе установки магнитного компаса равен 0,8 – 0,9. Если l меньше 0,3 то компас плохо работает даже в средних магнитных широтах. Хотя сила lН сама девиации не производит, но косвенно влияет на ее величину. В выражениях (24) 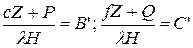 . Отсюда видно, что изменение lН ведет к изменению девиации.
. Отсюда видно, что изменение lН ведет к изменению девиации.
A’lH Предположим, что все коэффициенты кроме l и A’ равны нулю:
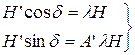
Возведем все в квадрат и сложим почленно:
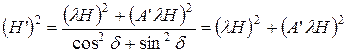
Это напоминает теорему Пифагора, так складываются два катета или два взаимно перпендикулярных отрезка. Поэтому, если lН совпадает с магнитным меридианом, то сила A’lH перпендикулярна ему. Причем, если А>0 то сила к востоку.

Сила A’lH сохраняет свое направление неизменным, независимо от курса судна, но создает девиацию, причем девиация эта постоянна. Коэффициент А можно уменьшить рациональной установкой комапса на судне.
B’lH Предположим, что все коэффициенты кроме l и B’ равны нулю:
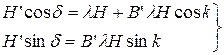
Возведем обе части уравнений в квадрат и сложим
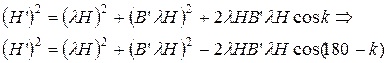
Данная формула выражает собой квадрат стороны H’ косоугольного треугольника, лежащий против угла 180°-к. Другими словами, это алгебраическое значение суммы двух векторов lН и В’lН, образующих между собой угол к равный магнитному курсу.
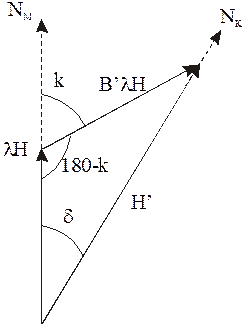
Отсюда видно, что сила B’lH действует относительно магнитного меридиана под углом, равным магнитному курсу. В судовых координатных осях она расположена по ДП. Сила производит девиацию, которая зависит от курса судна. Из формулы синуса девиации:
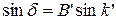
Отсюда видно, что d = 0 при к’ = 0°, 180°
d = max при к’ = 90°, 270°
При этом на одной половине окружности девиация положительна, на другой отрицательна, поэтому такая девиация называется полукруговой.
С’lH Предположим, что все коэффициенты кроме l и С’ равны нулю:
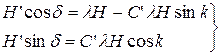
Как и с предыдущей силой, возведем в квадрат и просуммируем обе части и сделаем замену 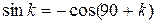 :
:
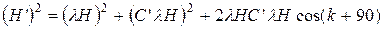
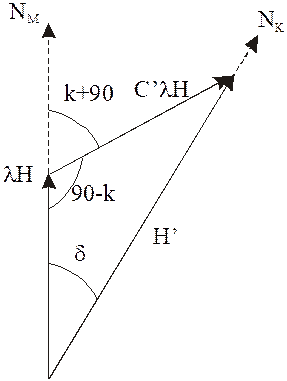
Следовательно сила C’lH перпендикулярна силе B’lH и составляет с магнитным меридианом угол, равный (к+90°). В судовых координатных осях она всегда перпендикулярна ДП. Из формулы синуса девиации:
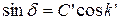
Отсюда видно, что d = max при к’ = 0°, 180°
d = 0 при к’ = 90°, 270°
То есть девиация от это силы также является полукруговой.
D’lH Предположим, что все коэффициенты кроме l и D’ равны нулю:
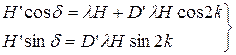
Возведем в квадрат обе части и сложим:
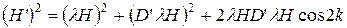
Это все та же формула квадрата стороны Н’ косоугольного треугольника. Эта сторона в данном случае лежит против угла (180 – 2к). Поэтому D’lH образует с магнитным меридианом угол 2к – удвоенный магнитный курс.

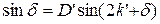
Если представить результат решения этого уравнения в виде графика, то будет видно, что девиация от силы D’lH при изменении курса на 360° четыре раза меняет свой знак, причем:
d = 0 при k’ = 0, 90, 180, 270
d = max при k’ = 45, 135, 225, 315
Такая девиация называется четвертной.
E’lH Предположим, что все коэффициенты кроме l и E’ равны нулю:
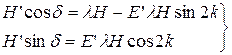
Возведем в квадрат обе части и сложим, заменим синус, как в силе С:
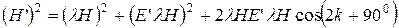
Отсюда видно, что при положительном значении сила E’lH направлена к магнитному меридиану под углом (2к+90°)
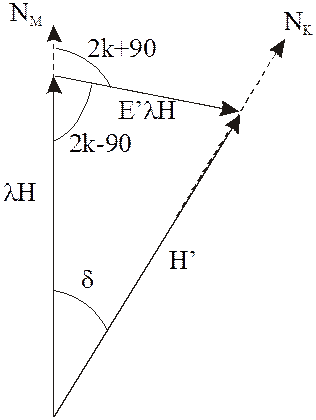
Аналогично силе D’lH сила E’lH производит четвертную девиацию.
Спроектируем все судовые силы на плоскость компасного меридиана:
Сила lН составляет с компасным меридианом угол -d, следовательно проекция равна lHcos(-d). Сила A’lH перпендикулярна силе lН и составляет с ней угол +90°, поэтому ее проекция на компасный меридиан равна A’lHcos(90-d). Сила B’lH направлена под углом К’ к компасному меридиану, следовательно ее проекция на меридиан B’lHcosk’. Перпендикулярная ей сила C’lH будет иметь проекцию на компасный меридиан C’lHcos(90°+k’).
Сила D’lH составляет с компасным меридианом угол (k’±k) или (2k’+d), следовательно ее проекция на компасный меридиан D’lHcos(2k’+d), а проекция перпендикулярной ей силы E’lHcos(90+2k’+d).
Сведем эти сведения в таблицу произведя некоторые тригонометрические преобразования.
| Силы | Угол с Nм | Угол с Nk | Проекция на Nk |
| lH | -d | lHcosd | |
| A’lH | 90° | 90° - d | A’lHsind |
| B’lH | k | k’ | B’lHcosk’ |
| C’lH | k+90° | k’ + 90° | -C’lHsink’ |
| D’lH | 2k | 2k’ + d° | D’lHcos(2k’+d) |
| E’lH | 2k+90° | 2k’ + d + 90° | -E’lHsin(2k’+d) |
Если все проекции сложить, то в результате получим результирующую H’ многоугольника сил:
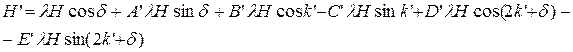 | (29) |
 2015-02-24
2015-02-24 3947
3947
