Кратные корни многочленов

Определение 1. Если в разложении многочлена 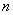-степени

,

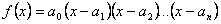некоторые множители окажутся одинаковыми, то

,

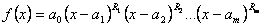
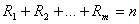то 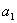-называется корнем кратности 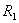, 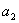-кратности 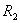и т.д.

Теорема 1. Если а является корнем многочлена 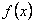кратности 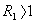, то для производной 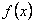это число является корнем кратности .

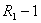Доказательство. Пусть

,

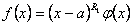где 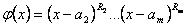не обращается в 0 при .

,

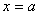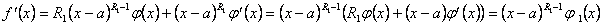т.е. 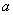является корнем кратности .

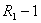Следствие. Число а является корнем кратности 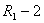для 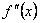,…, корнем кратности 1 для .

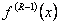37. Відділення кратних коренів.