Электрические токи в проводниках

Мы уже определили такие понятия, характеризующие направленное движение заряженных частиц, как сила тока (выражение 11.1), плотность тока. Установили уравнение непрерывности 22.1. Теперь же попробуем более подробно описать электрические токи в металлах, определить важнейшие параметры, характеризующие металлы с точки зрения их электропроводности.

Хорошая электропроводность металлов объясняется наличием в них почти свободных носителей заряда – электронов. В самом грубом приближении она равняется концентрации атомов в металле. Итак, будем считать, что концентрация свободных носителей заряда нам известна.

Классическая теория электропроводности металлов была создана в начале 20 века, однако во многих отношениях она полезна и сейчас, особенно для приближенных оценок. Квантовые теории физики твердого тела, несомненно, более строгие, но применять их весьма сложно.

§ 36 Классическая теория электропроводности металлов

Возьмем кусок проводника сечением 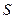, длиной 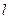. Концентрация свободных носителей заряда (электронов 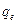, если это металлический проводник) равна 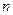. Будем поддерживать за счет внешнего источника постоянную разность потенциалов на концах проводника 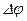(рис.36.1).

Рис.36.1

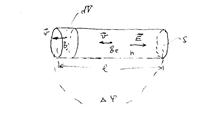
Если проводник однороден, то в нем будет существовать неисчезающее однородное электрическое поле напряженности 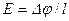. На свободные носители заряда в этом поле будет действовать кулоновская сила, под действием которой они придут в направленное движение вдоль поля. Скорость этого направленного движения будет конечной, поскольку в своем движении заряды будут рассеиваться на всевозможных дефектах. Назовем эту скорость средней скоростью направленного движения вдоль поля 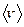. Ее часто называют дрейфовой скоростью. Свободный носитель заряда хаотически двигаясь с большой тепловой скоростью 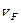медленно дрейфует по полю также, как парусник дрейфует по ветру под управлением неумелого экипажа.

Заряд, который пересечет сечение проводника за время 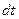, будет равен произведению заряда одного носителя 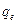на число свободных носителей заряда 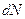, которые за это время пересекут сечение проводника. Например, левое сечение проводника пересекут все заряды из объема :

.

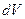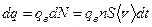Тогда плотность тока в проводнике будет равна:

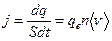. (36.1)

Для определения дрейфовой скорости решим задачу динамики движения свободного носителя заряда (электрона). Его ускорение в электрическом поле равно постоянной величине:

,

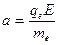скорость со временем растет линейно до тех пор, пока электрон не рассеится на каком-либо дефекте. После рассеяния среднее значение скорости в направлении электрического поля уменьшается. Процессы ускорения и рассеяния электронов иллюстрирует рис.36.2.

Рис.36.2

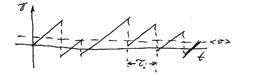
Найдем среднюю скорость, воспользовавшись ее определением (Механика, 3.6):

.

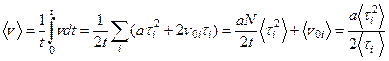Мы учли, что среднее значение начальной скорости после каждого рассеяния равно нулю, кроме этого, отношение длинного промежутка времени 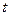, на котором мы усредняем скорость, к числу рассеяний за это время даст нам среднее время ускоренного движения электрона между столкновениями .

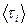Отношение 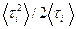называют временем релаксации .

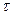Тогда окончательно для плотности тока в проводнике получим следующее выражение:

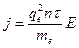. (36.2)

Сомножитель в правой части уравнения перед напряженностью поля зависит только от свойств материала проводника и называется удельной проводимостью 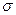. Ее, в свою очередь, представляют в виде произведения 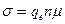, где

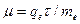(36.3)

называют подвижностью свободных носителей заряда. Она определяет дрейфовую скорость в единичном поле, так как .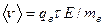

Уравнение 36.2 называют законом Ома в дифференциальной форме, поскольку оно в каждой точке внутри проводника связывает плотность тока с напряженностью поля. Можем получить закон Ома для участка цепи изображенной на рисунке 36.1 в интегральной форме:

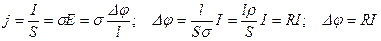. (36.4)

Падение напряжения на участке цепи 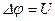равно произведению силы тока на сопротивление этого участка цепи 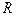. Последнее определяется следующим образом:

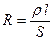, (36.5)

где величина 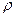обратная удельной проводимости 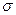называется удельным сопротивлением материала проводника.

Поскольку в своем дрейфовом движении носители заряда могут рассеиваться на различных дефектах, мы можем утверждать, что в общее удельное сопротивление будут давать вклады все возможные механизмы: рассеяние на тепловых колебаниях, на примесях, на вакансиях, на линейных дефектах кристаллов – дислокациях, рассеяние на границах между кристаллами в поликристаллическом материале.

Пусть у нас имеется 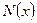электронов, движущихся вдоль оси х. Тогда число рассеянных электронов (выбывших из этой группы) после прохождения расстояния 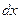будет пропорционально исходному их числу и длине пройденного ими пути

.

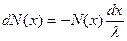Знак минус говорит об убывании числа электронов в группе, коэффициент пропорциональности 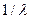характеризует материал проводника. Вероятность рассеяния электрона на единице длины пути будет пропорциональна :

.

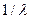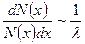Если процесс рассеяния на каждом дефекте независим от наличия других дефектов, то суммарная вероятность рассеяния (на единице длины) на каком либо дефекте будет равна сумме вероятностей рассеяния на определенном дефекте

.

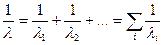Индекс 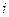соответствует определенному механизму рассеяния. Параметр 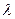- длина, на которой исходное число электронов в группе уменьшается в е раз, может быть названа длиной свободного пробега. Она, очевидно, пропорциональна времени релаксации 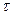: 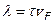. Коэффициент пропорциональности – средняя скорость теплового движения электронов 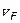. Тогда для удельного сопротивления получим выражение:

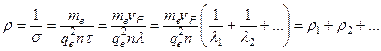. (36.6)

Электросопротивление металлов имеет аддитивную природу. Выражение (36.6) называют правилом Маттиссена (A.Mattiessen, 1862).

Этот физический результат применяется, например, для измерения концентрации примесей в сверхчистых металлах. Удельное сопротивление металла с ростом температуры растет (рис.36.3), поскольку увеличивается концентрация квазичастиц – фононов (тепловые колебания), на которых возможно рассеяние электронов.

Рис.36.3

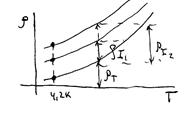
Измерив при низкой температуре 4.2К удельное сопротивление металла, можем по его значению судить о концентрации примесей, поскольку рассеяние на фононах становится незначительным. На рисунке приведены три кривые для трех концентраций примесей. Чем меньше 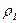, тем меньше содержание примесей в металле.