Задача установления невыполнимости множества предложений в огиике предикатов наиболее часто решается с помощью метода резолюций. Предварительно получают множество дизъюнктов так, как было описано ранее. В отличие от логики высказываний, для получения резольвент необходима унификация. Это не что иное, как получение частных случаев формул. Далее строят дерево опровержения, как в логике высказываний.
Невыполнимая в частном случае формула не может быть выполнима в других случаях, так как формула замкнута, а замкнутая формула либо ложна, либо истинна. На этом и основано использование метода резолюции в логике предикатов.
Например, для умозаключения по модусу «Barbara» при использовании формализации [8]:
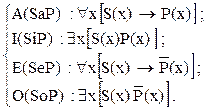

Получаем для умозаключения ААА по первой фигуре силлогизма конъюнкцию посылок и отрицания заключения: 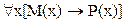
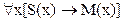
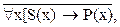 что соответствует
что соответствует
множеству дизъюнктов и дереву опровержения (рис. 120).

Рис. 120. Дерево опровержения для модуса «Barbara»
На рис. 120 «а» – это константа, получившаяся после введения функции Сколема при отрицании заключения модуса «Barbara».
Для модуса «Darapti» (третья фигура силлогизма) дизъюнкты и дерево опровержения имеют вид (рис. 121):
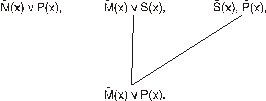
Рис. 121. Дерево опровержения для модуса «Darapti»
Опровержение не достигается, хотя модус правильный. Аналогично не достигается опровержение и для модусов «Felapton» и «Fesapo». Оказывается, это недостаток формализации, а не метода резолюций. В то же время формализация В.А. Смирнова [1]:
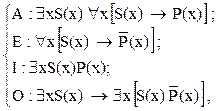
лишена этого недостатка. Так, для модуса «Felapton» (рис. 122):
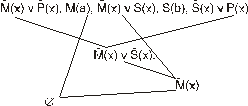
Рис. 122. Дерево опровержения для модуса «Felapton»
и модели В.А. Смирнова
Непосредственной проверкой можно убедиться в том, что при этой формализации метод резолюции «работает» для всех 19-ти правильных основных и 5-ти дополнительных модусов [1] и не «работает» для остальных 232-х неправильных.
На методе резолюций основан язык логического программирования ПРОЛОГ.
 2015-03-27
2015-03-27 1592
1592
