2015-03-08
1619
Пусть задан универсум U, тогда для любых множеств A, B, C, являющихся подмножеством U выполняются следующие свойства:
| 1) Идемпотентность: | A È A = A | A Ç A =A |
| 2) Комутативность: | AÈB=BÈA | AÇB=BÇA. |
| 3) Ассоциативность: | AÈ(BÈC) = (AÈB)ÈC | AÇ(BÇC)=(AÇB)ÇC. |
| 4) Дистрибутивность: | AÈ(BÇC)=(AÈB)Ç(AÈC) | AÇ(BÈC)=(AÇB)È(AÇC). |
| 5) Поглощение: | (AÇB)ÈA=A | (AÈB)ÇA=A. |
| 6) Свойство нуля: | AÈÆ =A | AÇ Æ=Æ. |
| 7) Свойство единицы: | AÈU=U | AÇU=A. |
| 8) Инволютивность: |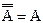 
| |
| 9) Законы де Моргана: | = È | = Ç. |
| 10) Свойства дополнения: | A È= U | A Ç= Æ. |
| 11) Свойство разности: | A \ B = A Ç |
В справедливости этих свойств можно убедиться различными способами, например нарисовать диаграммы Эйлера для левой и правой частей равенства и убедиться, что они совпадают, или же привести формальное рассуждение для каждого равенства.
