Исследование функции будем проводить по плану.
1. Найдем О.Д.З. и, если есть асимптоты О.Д.З., 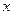 – любое. Следовательно, нет
– любое. Следовательно, нет
точек разрыва, поэтому вертикальных асимптот нет.
2. Найдем точки пересечения графика функции с осями координат, исследуем функцию на четность, тригонометрические функции - на периодичность. Пусть 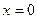 , тогда
, тогда 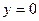 . Точка (0,0). Проверим четность функции.
. Точка (0,0). Проверим четность функции.
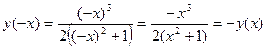 . Значит, наша функция нечетная, и ее график симметричен относительно начала координат.
. Значит, наша функция нечетная, и ее график симметричен относительно начала координат.
3. Исследуем монотонность функции с помощью 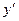 .
.
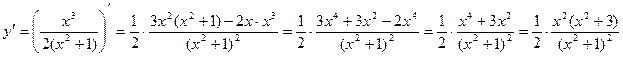
|
|

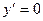 при
при 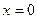
 |
+ +


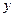 0 х
0 х
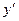 равен нулю или бесконечности.
равен нулю или бесконечности.
4. С помощью 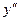 находим точки перегиба
находим точки перегиба
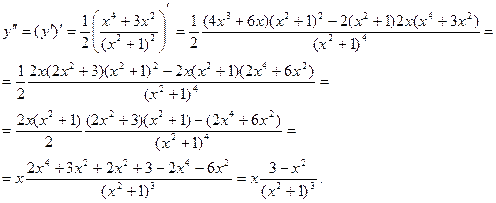
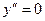 при
при 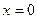 и
и 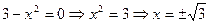 .
.
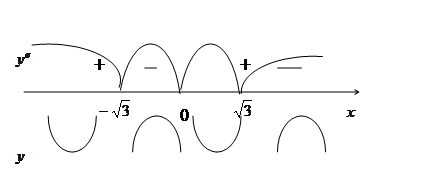 |
Все точки, в которых 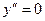 , являются точками перегиба, так как в них
, являются точками перегиба, так как в них 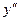 меняет знак на противоположный.
меняет знак на противоположный.
Найдем значения функции в этих точках: 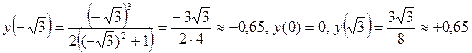 .
.
5. Найдем наклонные асимптоты, если они есть 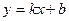 .
.
Сначала 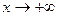 , тогда
, тогда 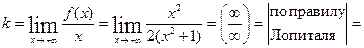
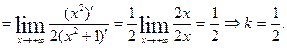 Теперь найдем
Теперь найдем 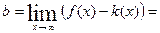
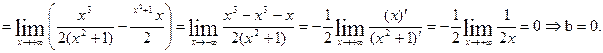
Получаем 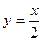 - уравнение правой асимптоты. Повторяя прежние рассуждения, уже при
- уравнение правой асимптоты. Повторяя прежние рассуждения, уже при 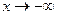 получим уравнение левой асимптоты
получим уравнение левой асимптоты 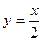 .
.
6. Теперь строим график функции, начертив сначала все асимптоты, отметив точки экстремума, точки перегиба и точки пересечения с осями координат.
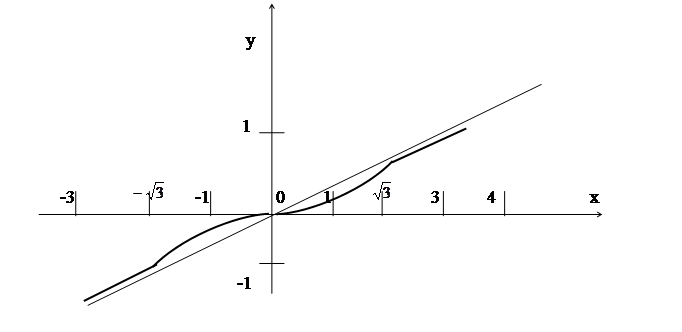
Контрольные варианты к задаче 7.
Исследовать функцию и построить ее график:
1. 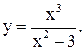
| 2. 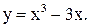
| 3. 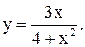
| 4. 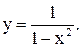
|
5. 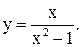
| 6. 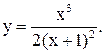
| 7. 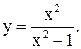
| 8. 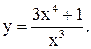
|
9. 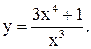
| 10. 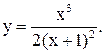
| 11. 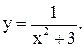
| 12. 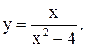
|
13. 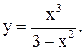
| 14. 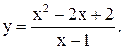
| 15. 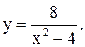
| 16. 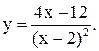
|
17. 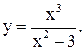
| 18. 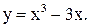
| 19. 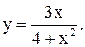
| 20. 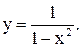
|
21. 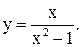
| 22. 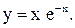
| 23. 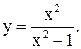
| 24. 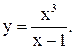
|
25. 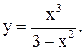
| 26. 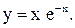
| 27. 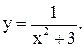
| 28. 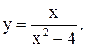
|
29. 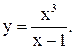
| 30. 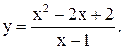
|
 2015-03-08
2015-03-08 230
230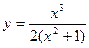 всюду возрастающая, не имеющая точек экстремума, так как нет ни одной точки, в которой
всюду возрастающая, не имеющая точек экстремума, так как нет ни одной точки, в которой







