2015-03-20
295При плануванні експерименту проводять перетворення розмірних керованих незалежних чинників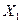 
в безрозмірні, нормовані:
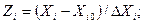
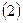
це дає можливість легко побудувати ортогональну МП і значно полегшує подальші розрахунки, оскільки в цьому випадку верхні і нижні рівні варіювання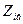 
і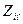 
у відносних одиницях рівні відповідно +1 і -1 незалежно від фізичної природи чинників, значень основних рівнів і інтервалів варіювання факторів 
.
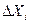Якщо для трьох факторів задати теоретичне рівняння регресії відносно нормованих факторів має вигляд
, 
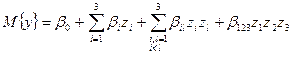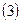
тобто ступенями факторів вище за першу можна знехтувати, то ПФЕ дає можливість знайти роздільні оцінки коефіцієнтів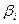 
. Оскільки зміна вихідної величини 
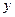носить випадковий характер, то є можливість визначити лише вибіркові коефіцієнти регресі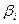ї і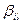 
для оцінювання теоретичних коефіцієнтів , .
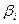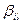У разі ОЦКП критерієм оптимальності плану є ортогональность стовпців МП. Через ортогональністі планування всі оцінки коефіцієнтів визначаються незалежно один від одного.
2.2 Планування. Вказаний вище критерій оптимальності плану приводить до побудови МП з ортогональними вектор стовпцями, у тому числі і для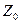 
і 
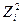. Ортогоналізацію стовпців 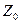і 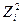проводять за допомогою перетворення
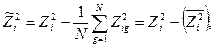
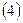
де N — загальне число рядків МП. неважко помітити, що в цьому випадку умова ортогональності виконується, тобто
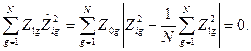
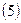
Окрім стовпців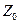 
і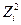 
ортогоналізації підлягають вектор-стовпц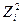і і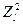 
. З умови ортогональності перетворених вектор-стовпців 
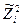і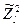 
, має вигляд
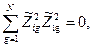
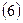
виводиться рівняння для розрахунку величини зіркового плеча:
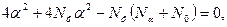
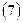
де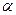 
— величина зоряного плеча; 
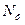— число крапок ПФЕ (ДФЕ); 
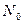— число центральних точок; 
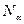— число «зіркових точок» крапок для квадратів
В табл. 7.2 приведені параметри ОЦКП для числа чинників n = 2; 3; 4
Таблиця 2.
| n |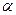
|
|
|
| 
|
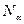
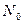
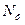
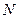
| 1,0 | |||||
| 1,215 | |||||
| 1,414 |
| Групы точек | g |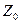
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
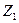
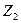
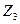
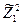
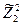
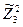
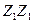
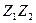
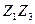
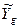
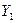
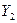
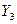
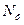
| +1 +1 +1 +1 +1 +1 +1 +1 | -1 +1 -1 +1 -1 +1 -1 +1 | -1 -1 +1 +1 -1 -1 +1 +1 | -1 -1 -1 -1 +1 +1 +1 +1 | 0,27 0,27 0,27 0,27 0,27 0,27 0,27 0,27 | 0,27 0,27 0,27 0,27 0,27 0,27 0,27 0,27 | 0,27 0,27 0,27 0,27 0,27 0,27 0,27 0,27 | +1 -1 -1 +1 +1 -1 -1 +1 | +1 -1 +1 -1 -1 +1 -1 +1 | +1 +1 -1 -1 -1 -1 +1 +1 | |||||
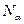
| +1 +1 +1 +1 +1 +1 | -1,215 +1,215 | -1,215 +1,215 | -1,215 +1,215 | +0,75 +0,75 -0,73 -0,73 -0,73 -0,73 | -0,73 -0,73 +0,75 +0,75 -0,73 -0,73 | -0,73 -0,73 -0,73 -0,73 +0,75 +0,75 | ||||||||
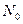
| +1 | -0,73 | -0,73 | -0,73 |
Матриця ОЦКП для трьох незалежних змінних приведена в табл.3, де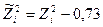 
. Таблиця 7.3
2.3 Проведення експерименту. Точно так, як і при проведенні ПФЕ, через випадковий характер зміни вихідної величини в кожній g—ой точці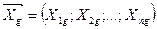 
(де g=1,2., N), доводиться проробляти m паралельних дослідів і результати спостереженнь усереднювати:
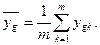
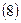
Варіанти варіювання в кожній серії випробувань або всі досліди всіх m серій рандомізують.
2.4 Перевірка відтворності експерименту є не що інше, як перевірка виконання другої передумови регресійного аналізу про однорідність вибіркових дисперсій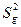 
. Задача полягає в перевірці гіпотези про рівність генеральних дисперсій 
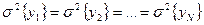при дослідах відповідно в крапках 
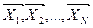. Оцінки дисперсій знаходять по відомій формулі
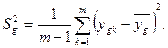
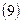
Оскільки всі оцінки дисперсій одержані по вибірках однакового об'єму m=3, то число ступенів свободи для всіх них однакове і складає
. 
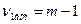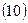
В цьому випадку для перевірки гіпотези про однорідність оцінок 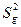дисперсій слід користуватися критерієм Кохрена, який заснований на законі розподілу відношення максимальної оцінки дисперсії до суми всіх порівнюваних оцінок дисперсій, тобто
. 
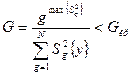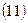
Якщо обчислене за даними експерименту (емпіричне) значення критерію G виявиться менше критичного значення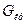 
, знайденого по таблиці (див. Додаток X або ХІ) для 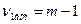і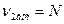 
в даному випадку 
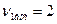і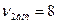 
) і вибраного рівня значущості 
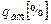(звичайно 5%), то гіпотеза про однорідність вибіркових дисперсій відповідає результат спостережень. При цьому всю групу вибіркових дисперсій можна вважати оцінками для однієї і тієї ж генеральної дисперсії 
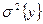відтворності експерименту, звідки якнайкраща її оцінка має вигляд
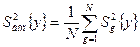
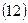
з числом ступенів свободи
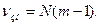
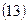
Якщо перевірка відтворності експерименту дала негативний результат, то залишається визнати його не відтворюваність відносно керованих факторів унаслідок наявності несприятливих флуктуації некерованих і неконтрольованих чинників. При цьому необхідно або збільшити число паралельних дослідів для варіантів варіювання з великими значеннями вибіркових дисперсій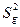 
, або використовувати надалі модифікацію методу найменших квадратів, придатну при невиконанні передумови про відтворність експерименту.
2.5 Отримання математичної моделі об'єкту. Оцінки коефіцієнтів рівняння регресії визначають по формулі
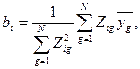
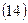
а дисперсії оцінок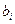 
коефіцієнтів — по формулі
. 
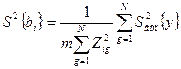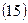
Оскільки знаменник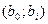 
у формулах (14) і (15) в загальному випадку різний для різних груп оцінок коефіцієнтів 
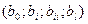, то оцінки дисперсії ( 15 ) однакові тільки всередині даної групи оцінок коефіцієнтів.
