С понятием модуля учащиеся знакомятся в курсе математики в 6 классе. Здесь же встречаются уравнения и неравенства вида: 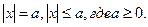 В дальнейшем задания, содержащие модуль встречаются при решении линейных уравнений и построении графиков линейных функций.
В дальнейшем задания, содержащие модуль встречаются при решении линейных уравнений и построении графиков линейных функций.
Изучение данного курса позволит расширить круг задач, решаемых учащимися, углубить содержание их математического образования.
Программа курса содержит теоретический материал, разбитый на три блока. В каждом из блоков приведены образцы решений наиболее типичных заданий и дана подборка заданий для коллективной или самостоятельной работы учащихся, цель которой – закрепление и проверка знаний учащихся по данной теме. В задания также включены решения квадратных уравнений и неравенств второй степени с одной переменной, содержащих модули, а также построение графиков квадратичных функций с модулем.
ЦЕЛЬ КУРСА: Познакомить учащихся с решением уравнений и неравенств, содержащих модули, с построением графиков функций с модулем;
|
|
|
расширить математический кругозор учащихся, повысить их готовность к изучению математики на повышенном уровне.
Дидактические материалы курса
I. 1. Понятие модуля числа. Свойства модулей.
Модуль числа а обозначается 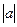 .
.
Модуль положительного числа равен самому числу. 
Например:|3|= 3; | 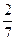 |=
|= 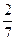 ; |2,4|= 2,4
; |2,4|= 2,4
1) Модуль отрицательного числа равен противоположному ему числу.
Например: |-2| = -(-2)= 2; |- 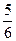 |= -(-
|= -(- 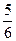 )=
)= 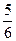
2) Модуль нуля равен нулю: |0|= 0.
Определение модуля числа можно записать в виде:
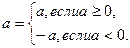
Рассмотрим геометрический смысл модуля числа.
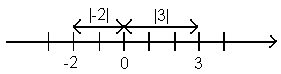 Изобразим на числовой прямой, например, точки 3 и -2.
Изобразим на числовой прямой, например, точки 3 и -2.
Из рисунка видно, что |3|=3 есть расстояние в единичных отрезках от точки 0 до точки 3; а |-2|=2 есть расстояние в единичных отрезках от точки 0 до точки -2.
Итак, геометрически 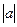 есть расстояние в единичных отрезках от точки 0 до точки, изображающей число а.
есть расстояние в единичных отрезках от точки 0 до точки, изображающей число а.
Свойства модулей.
1. 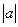
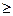 0 4.
0 4. 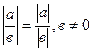
2. 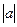 =
= 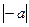 5.
5. 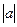 2= а 2
2= а 2
3. 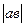 =
= 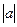
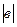
2. Линейные уравнения, содержащие неизвестное под знаком модуля.
Задача 1. Решить уравнение:
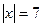
Решение. I способ.
а) Пусть х 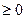 , тогда по определению модуля
, тогда по определению модуля 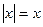 , уравнение примет вид: х= 7; 7- корень уравнения;
, уравнение примет вид: х= 7; 7- корень уравнения;
б) пусть x<0, тогда по определению модуля 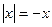 ; уравнение примет вид:- х= 7; х= -7;
; уравнение примет вид:- х= 7; х= -7;
-7- корень уравнения.
Ответ: 7; -7.
Решение. II способ.
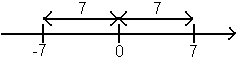
Это уравнение можно решить геометрически, считая 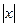 , как расстояние в единичных отрезках от точки х до точки 0; так как оно равно 7, то это могут быть точки 7 и -7.
, как расстояние в единичных отрезках от точки х до точки 0; так как оно равно 7, то это могут быть точки 7 и -7.
Если уравнение содержит переменную или функцию этой переменной под знаком модуля, то уравнение вида 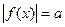 , где
, где 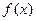 – функция переменной
– функция переменной 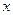 , а – действительное число, при a <0 не имеет корней, при a =0 равносильно уравнению
, а – действительное число, при a <0 не имеет корней, при a =0 равносильно уравнению 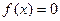 , при a >0 равносильно совокупности уравнений:
, при a >0 равносильно совокупности уравнений:
|
|
|
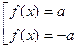
Задача 2. Решить уравнение
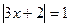
1) если 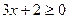 , то
, то 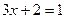
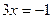
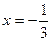
2) если 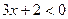 , то
, то 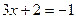
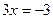
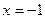
Ответ: 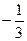 ;
; 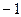 .
.
Задание. Решить уравнения:
а) 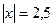 д)
д) 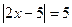
б) 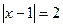 е)
е) 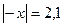
в) 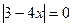 ж)
ж) 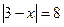
г) 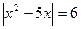 (Ответ: 2;3;–1;6)
(Ответ: 2;3;–1;6)
3) Линейные неравенства, содержащие неизвестное под знаком модуля.
Рассмотрим неравенство 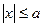 , где а > 0.
, где а > 0. 
Этому неравенству удовлетворяют все точки х, находящиеся на расстоянии, не большим а, от точки 0, т.е. точки отрезка 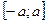 .
.
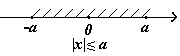
Отрезок 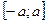 - это множество чисел х, удовлетворяющих двойному неравенству – а
- это множество чисел х, удовлетворяющих двойному неравенству – а 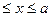 .
.
Следовательно, неравенство 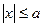 , где а > 0, означает то же самое, что и двойное неравенство – а
, где а > 0, означает то же самое, что и двойное неравенство – а 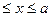 .
.
Например: 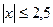 , равносильно -2,5
, равносильно -2,5 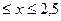 .
.
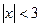 , равносильно -3 < x < 3.
, равносильно -3 < x < 3.
Задача 3. Решить неравенство: 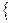 | 5- 3x | < 8
| 5- 3x | < 8
I способ: II способ:
-8 < 5 – 3x < 8
-8 -5 < - 3x < 8 – 5
- 13 < - 3x < 3
- 1< x < 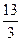 .
.
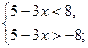
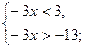
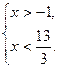 Ответ:
Ответ: 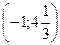
Рассмотрим неравенство 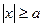 , где а >0.
, где а >0.
Этому неравенству удовлетворяют все точки х. находящиеся на расстоянии, не меньше а, от точки 0, т. е. точки двух лучей х 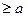 и х
и х 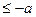 .
.
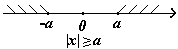
Например: |x| > 3, равносильно х > 3 и х < -3.
Задача 4. Решите неравенство: 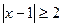
а) если х-1 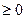 , то х -1
, то х -1 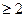 , получим систему неравенств:
, получим систему неравенств:
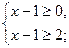
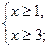 х
х 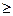 3 Ответ: [ 3; ∞].
3 Ответ: [ 3; ∞].
б) если х–1 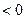 , то
, то 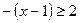
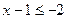
Получим систему неравенств
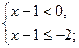
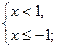 х
х 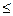 –1
–1
Ответ: 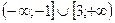
Отметим, что если в неравенстве 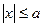 , число a =0, то неравенство имеет единственное решение
, число a =0, то неравенство имеет единственное решение 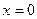 , а если
, а если 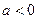 , то неравенство не имеет решений.
, то неравенство не имеет решений.
Если в неравенстве 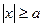 число
число 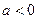 , то любое число является его решением, если a =0, то решение единственное
, то любое число является его решением, если a =0, то решение единственное 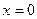 .
.
Задание 1. Изобразите на числовой прямой множество решений неравенства:
1) 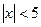 2)
2) 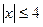 3)
3) 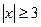 4)
4) 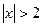
Задание 2. Запишите неравенство с модулем в виде двойного неравенства:
1) 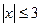 2)
2) 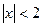
Задание 3. Двойное неравенство запишите в виде одного неравенства с модулем:
1) 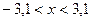 2)
2) 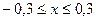
Задание 4. Решите неравенство:
1) 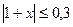 3)
3) 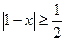 5)
5) 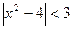 (Ответ:
(Ответ: 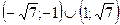 )
)
2) 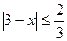 4)
4) 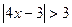 6)
6) 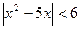 (Ответ:
(Ответ: 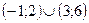 )
)
Задание 5. Найдите все целые значения x, при которых выполняется неравенство:
1) 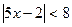 1)
1) 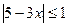
Задание 6. Решите систему неравенств и найдите сумму его целых решений:
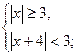 Ответ:
Ответ: 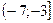 ; сумма целых решений: –18.
; сумма целых решений: –18.
Задача 4. Решить уравнение: | 2x - 8 | = 3x + 1.
а) Если 2x - 8 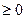 , то 2х – 8 = 3х +1
, то 2х – 8 = 3х +1
х 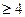 , 2х – 3х = 8 + 1
, 2х – 3х = 8 + 1
– х = 9
х = – 9
однако при х = – 9 не выполняется неравенство х 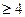 , значит – 9, не является корнем данного уравнения
, значит – 9, не является корнем данного уравнения
б) если 2х – 8 < 0, то –(2х – 8) = 3х + 1
х < 4 8 – 2х = 3х + 1
х = 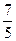 = 1
= 1 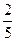
х = 1 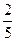 удовлетворяет неравенству х < 4, значит 1
удовлетворяет неравенству х < 4, значит 1 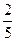 - корень уравнения.
- корень уравнения.
Ответ: 1 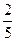
Задание: Решить уравнения
а) | х + 1| = 2 – х Ответ: 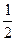
б) | х – 3| = 2х + 1 Ответ: 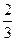
в) | х + 3| = х + 3 Ответ: х 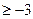
г) | х – 2| = 2 – х Ответ: х 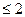
д) х2 + 5 | х | – 6 = 0 Ответ: 1; – 1
Задача 5. Решить неравенство: |2х + 4| 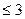 х + 2
х + 2
Данное неравенство можно заменить совокупностью двух систем:
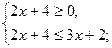 или
или 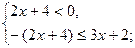
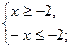
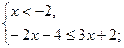
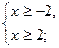 х
х 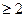
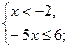
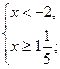 , нет решения
, нет решения
Ответ: [2; + 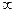 ).
).
Задание. Решить неравенство:
а) |х – 2| > х + 3 Ответ: 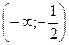
б) |2х – 6| < 9х – 5 Ответ: (1; + 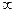 )
)
в) 3|х + 1| 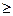 х + 5 Ответ: (
х + 5 Ответ: (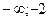 ]
] 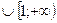
г) |х – 6| > х2 – 5х + 9 Ответ: (1; 3)
II Решение уравнений и неравенств, содержащих несколько модулей.
Для решения уравнения или неравенства вида |f1(x)| 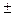 |f2(x)|
|f2(x)| 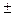 …
… 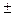 |fn(x)|
|fn(x)| 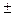
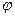 (x) = 0 (
(x) = 0 (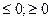 ), где fi(x) (i = 1, 2, …, n),
), где fi(x) (i = 1, 2, …, n), 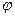 (x) – непрерывные функции переменных, используют метод “раскрытия” на непересекающихся промежутках.
(x) – непрерывные функции переменных, используют метод “раскрытия” на непересекающихся промежутках.
Суть метода состоит в следующем:
1) Находят те значения переменной, при которых рассматриваемые модули равны 0, т.е. решаем уравнения f1(x) = 0, …, fn(x) = 0.
2) Пусть x1, x2,…xk – корни этих уравнений. Нанесем эти корни на числовую прямую. Они разбивают прямую на (k + 1) промежутков.
3) Если функции f1(x),…,fn(x) непрерывны на всей числовой прямой, тогда значения этих функций будут сохранять свои знаки на каждом из указанных промежутков. Определим знак, который имеет выражение, стоящее под знаком модуля, на каждом из этих промежутков.
4) Пользуясь определением модуля, раскрывают на каждом из этих участков все знаки модулей и решают получившиеся уравнения или неравенства.
5) Отобрать из полученных решений все те решения, которые принадлежат рассматриваемому промежутку.
6) В ответе указать объединение всех решений, полученных на каждом из участков.
|
|
|
Задача 1. Решить неравенство:
|х – 1| + |х – 2| > 3 + х
х – 1 = 0; х – 2 = 0
х = 1 х = 2
Отметим на числовой прямой числа 1 и 2. Эти числа разбивают числовую прямую на 3 промежутка: х 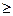 2; 1
2; 1 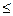 х<2; x < 1.
х<2; x < 1.
Определим знаки выражений, стоящих под знаком модуля на каждом из промежутков.
Чтобы определить знак значений f1(x),…fn(x) на любом из промежутков (xi-1; xi), достаточно вычислить f1(x),…fn(x) в любой точке х0 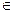 (xi-1; xi) знаки этих чисел совпадают со знаками значений f1(x),…fn(x) соответственно на всем промежутке.
(xi-1; xi) знаки этих чисел совпадают со знаками значений f1(x),…fn(x) соответственно на всем промежутке.
| x– 1 | – | + | + |
| x– 2 | – 1 | – 2 | + |
1) если 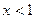 , то:
, то: 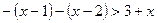
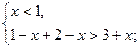
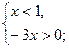
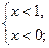
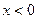
2) если 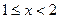 , то:
, то: 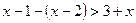
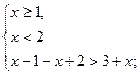
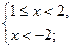 нет решений
нет решений
3) если 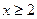 , то:
, то: 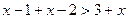
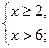
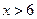
Ответ: 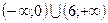 .
.
Задача 2. Решить уравнение
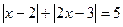
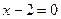 и
и 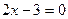
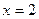
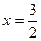
| x– 2 | – | – | + |
| 2 x– 3 | – 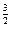
| + 
| + |
1) если 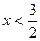 , то:
, то: 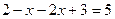 ,
,
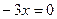 ,
,
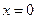 – решение
– решение
2) если 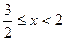 , то:
, то: 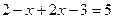
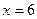
3) если 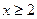 , то:
, то: 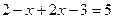
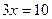
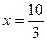
Ответ: 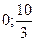 .
.
Задание:
1) решить уравнение:
а) 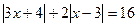 (Ответ:
(Ответ: 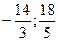 ) в)
) в) 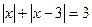 (Ответ:
(Ответ: 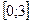 )
)
б) 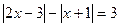 (Ответ:
(Ответ: 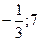 ) г)
) г) 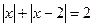 (Ответ:
(Ответ: 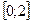 )
)
2) решить неравенство:
а) 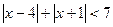 (Ответ:
(Ответ: 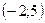 )
)
б) 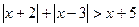 (Ответ:
(Ответ: 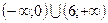 )
)
в) 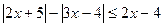 (Ответ:
(Ответ: 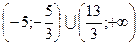 )
)
III Построение графиков функций, содержащих модуль
Пример 1. Построить график функции 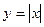
а) если 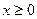 , то
, то 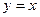 , графиком этой функции является биссектриса I координатного угла.
, графиком этой функции является биссектриса I координатного угла.
б) если 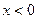 , то
, то 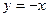 , графиком этой функции является биссектриса II координатного угла.
, графиком этой функции является биссектриса II координатного угла.
Объединив эти графики, получим график 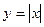 для
для 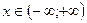
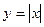
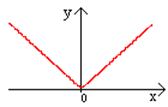
При построении графика функции 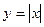 можно пользоваться четностью функции.
можно пользоваться четностью функции.
Если 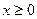 , то
, то 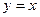 – графиком – биссектриса I координатного угла, так как
– графиком – биссектриса I координатного угла, так как 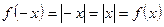 , то функция
, то функция 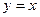 – четная, её график симметричен относительно оси
– четная, её график симметричен относительно оси 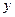 .
.
Поэтому биссектрису I координатного угла отобразим симметрично оси 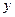 .
.
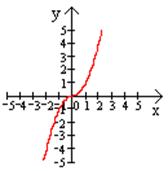
Пример 2. Построить график функции 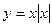
Если 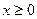 , то
, то 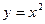 . Графиком будет ветвь параболы. Так как
. Графиком будет ветвь параболы. Так как 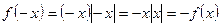 , то функция
, то функция 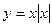 – нечетная, значит график её симметричен относительно начала координат. Поэтому подвергнем ветвь параболы преобразованием симметрии относительно начала координат.
– нечетная, значит график её симметричен относительно начала координат. Поэтому подвергнем ветвь параболы преобразованием симметрии относительно начала координат.
Геометрические преобразования графиков
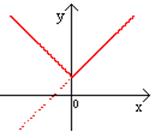
1) В общем виде график функции 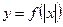 получается из графика функции
получается из графика функции 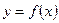 следующим образом: при
следующим образом: при 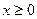 график
график 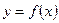 – сохраняется, а при
– сохраняется, а при 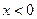 полученная часть графика отображается симметрично относительно оси
полученная часть графика отображается симметрично относительно оси 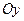 .
.
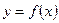
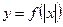
2) График функции 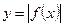 получается из графика функции
получается из графика функции 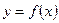 следующим образом: часть графика
следующим образом: часть графика 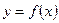 , лежащая над осью
, лежащая над осью 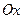 , сохраняется, часть его, лежащая под осью
, сохраняется, часть его, лежащая под осью 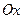 , отображается симметрично относительно оси
, отображается симметрично относительно оси 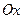 .
.
|
|
|
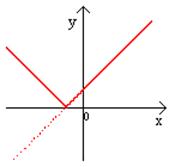
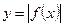
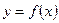
Пример 3. Построить график функции 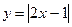
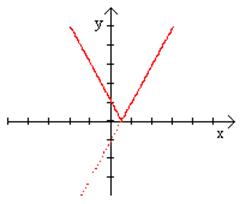 если
если 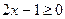 , то
, то 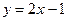
| x | 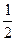
| ||
| y |
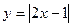
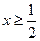
если 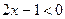 , то
, то 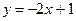 1 1
1 1
| x | |
| y |
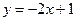
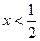
3) Построение графика функции 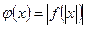
Сначала применить правило 1, затем 2.
Пример 4. 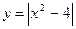
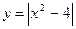
1
Пример 5. 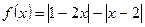
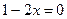 и
и 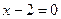
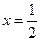
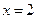
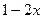
| + | – | – |
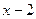
| – 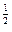
| – 
| + |
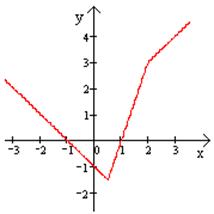
| x | -1 | |
| y | -1 |
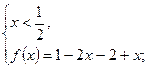
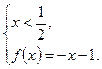
| x | 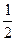
| |
| y | 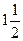
|
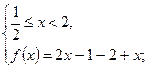
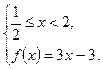
| x | ||
| y |
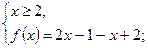
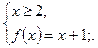
Задание:
1) Постройте график функции: а) 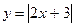 ; б)
; б) 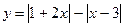
2) Изобразите на плоскости множество точек, координаты которых удовлетворяют условиям:
а) 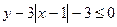 б)
б) 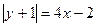 в)
в) 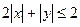
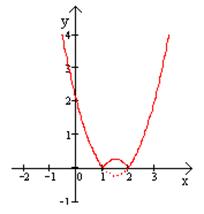
Построить график:
а) 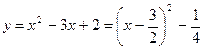 б)
б) 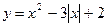
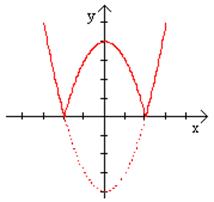
Координаты вершины параболы: 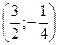 .
.
Точки пересечения с осью Х: х = 1 и х = 2
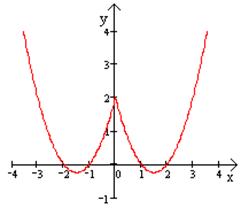
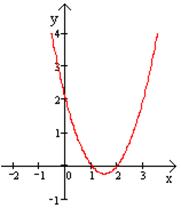
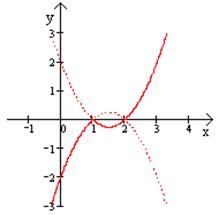
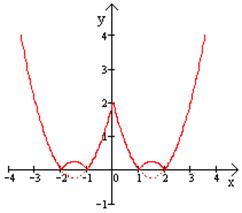 в)
в) 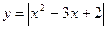 г)
г) 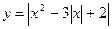
д) 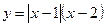
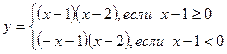
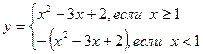
Пример. Решить уравнение:
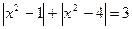
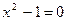
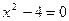
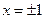
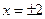
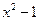
| + | + | – | + | + |
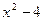
| + –2 | – –1 | – 1 | – 2 | + |
1) 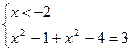
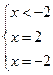 нет решений
нет решений
2) 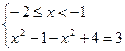
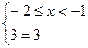
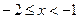
3) 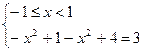
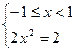
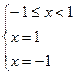
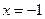
4) 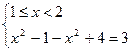
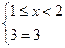
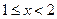
5) 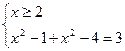
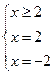
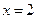
 Ответ:
Ответ: 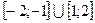
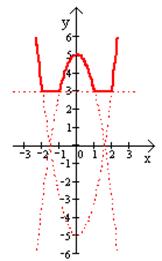
Пример. Построить график функции
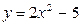 |
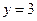 |
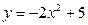
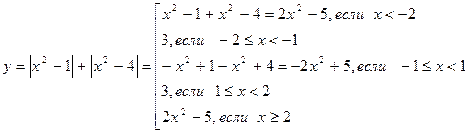
Задание: построить графики функций
а) y = 2x – 4 б) y = |2x – 4|
в) y = 2 |x| – 4 г) y = |2|x| – 4|
Литература
- Алимов Ш. А. Алгебра 8 кл. – Москва, Просвещение, 1991
- Виленкин Н. Я. Алгебра 9 кл. – Москва, Просвещение, 1998
- Гусак Г. М. Математика для подготовительных отделений вузов. Минск Вышэйшая школа, 1989
- Кравцев С. В. Методы решения задач по алгебре. Москва. Экзамен., 2003
- Черкасов О. Ю. Математика. Скорая помощь абитуриенту. Москва. Московский лицей, 1995
 2015-04-08
2015-04-08 376
376






