№1. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
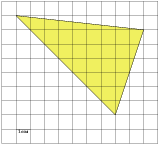
Решение. Площадь треугольника равна разности площади прямоугольника и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому
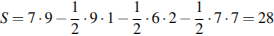 см2. Ответ: 28.
см2. Ответ: 28.
№2.
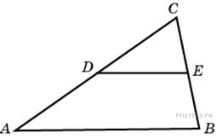 Площадь треугольника ABC равна 136. DE — средняя линия. Найдите площадь треугольника CDE.
Площадь треугольника ABC равна 136. DE — средняя линия. Найдите площадь треугольника CDE.
Решение. Средняя линия треугольника отсекает от него подобный треугольник с коэффициентом 0,5. Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому площадь отсеченного треугольника вчетверо меньше площади исходного. Таким образом, площадь треугольника CDE равна 34.
Ответ: 34.
№3. Площадь треугольника равна 217, а его периметр 62. Найдите радиус вписанной окружности.
Решение. Площадь треугольника равна произведению полупериметра на радиус вписанной окружности, поэтому 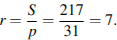 Ответ: 7.
Ответ: 7.
№4. 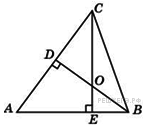 В треугольнике
В треугольнике  угол
угол  равен
равен  , а углы
, а углы  и
и  – острые.
– острые. 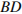 и
и  – высоты, пересекающиеся в точке
– высоты, пересекающиеся в точке  . Найдите угол
. Найдите угол 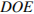 . Ответ дайте в градусах.
. Ответ дайте в градусах.
Решение. Cумма углов в выпуклом четырехугольнике равна 360 градусам, следовательно,
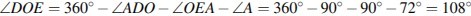 . Ответ: 108.
. Ответ: 108.
№5.
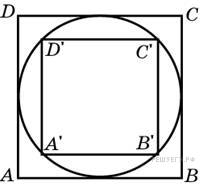 Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность? Решение.
Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность? Решение.
Пусть радиус окружности равен R. Тогда сторона описанного вокруг нее квадрата равна 2 R, а его площадь, равная квадрату стороны, равна 4 R 2. Диагональ вписанного квадрата также равна 2 R, поэтому его площадь, равная половине произведения диагоналей, равна 2 R 2. Следовательно, отношение площади описанного квадрата к площади вписанного равно 2. Ответ: 2.
№6. Две стороны прямоугольника 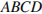 равны 6 и 8. Найдите длину вектора
равны 6 и 8. Найдите длину вектора 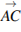 .
.
Решение. Вектор 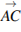 образует в прямоугольнике два прямоугольных треугольника. Поэтому по теореме Пифагора
образует в прямоугольнике два прямоугольных треугольника. Поэтому по теореме Пифагора 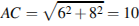 . Ответ: 10.
. Ответ: 10.
№7.
 Две стороны прямоугольника
Две стороны прямоугольника 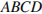 равны 6 и 8. Найдите длину суммы векторов
равны 6 и 8. Найдите длину суммы векторов 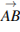 и
и 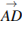 .
.
Решение. Сумма векторов 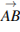 и
и 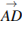 равна вектору
равна вектору 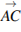 . Вектор
. Вектор 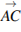 образует в прямоугольнике два прямоугольных треугольника. Поэтому по теореме Пифагора
образует в прямоугольнике два прямоугольных треугольника. Поэтому по теореме Пифагора 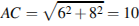 . Ответ: 10.
. Ответ: 10.
№8.
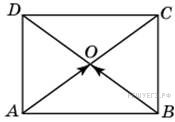 Две стороны изображенного на рисунке прямоугольника
Две стороны изображенного на рисунке прямоугольника 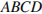 равны 6 и 8. Диагонали пересекаются в точке
равны 6 и 8. Диагонали пересекаются в точке  . Найдите длину суммы векторов
. Найдите длину суммы векторов 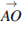 и
и 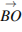 . Решение. Сумма векторов
. Решение. Сумма векторов 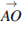 и
и 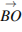 равна вектору
равна вектору 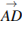 . Его длина равна 6. Ответ: 6.
. Его длина равна 6. Ответ: 6.
№9.
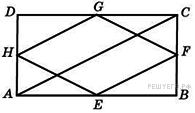 Середины сторон прямоугольника, диагональ которого равна 5, последовательно соединены отрезками. Найдите периметр образовавшегося четырехугольника.
Середины сторон прямоугольника, диагональ которого равна 5, последовательно соединены отрезками. Найдите периметр образовавшегося четырехугольника.
Решение. Четырехугольник 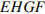 ромб, значит, его периметр равен
ромб, значит, его периметр равен 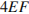 . Стороны искомого четырехугольника равны средним линиям треугольников, образуемых диагоналями и сторонами данного четырехугольника. Таким образом, стороны искомого четырехугольника равны половинам диагоналей. Соответственно, имеем:
. Стороны искомого четырехугольника равны средним линиям треугольников, образуемых диагоналями и сторонами данного четырехугольника. Таким образом, стороны искомого четырехугольника равны половинам диагоналей. Соответственно, имеем: 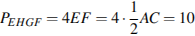 . Ответ: 10.
. Ответ: 10.
№10.
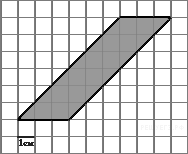 Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Решение.
Площадь параллелограмма равна произведению основания на высоту, проведенную к этому основанию или его продолжению. Поэтому 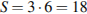 см2. Ответ: 18.
см2. Ответ: 18.
№11.
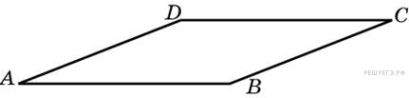 Найдите площадь параллелограмма, если две его стороны равны 47 и 2, а угол между ними равен 30°.
Найдите площадь параллелограмма, если две его стороны равны 47 и 2, а угол между ними равен 30°.
Решение. Площадь параллелограмма равна произведению его сторон на синус угла между ними. Поэтому 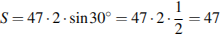 см2. Ответ: 47.
см2. Ответ: 47.
№12.
 Боковая сторона равнобедренного треугольника равна 10. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.
Боковая сторона равнобедренного треугольника равна 10. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.
Решение. так как прямые, проведенные из основания треугольника 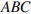 параллельны его сторонам, то углы в треугольниках
параллельны его сторонам, то углы в треугольниках 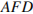 и
и 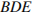 равны углам треугольника
равны углам треугольника 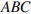 . Треугольники подобны, соответственно, они равнобедренные. Противоположные стороны параллелограмма
. Треугольники подобны, соответственно, они равнобедренные. Противоположные стороны параллелограмма 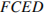 попарно равны, значит
попарно равны, значит
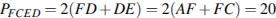 . Ответ: 20.
. Ответ: 20.
№13. 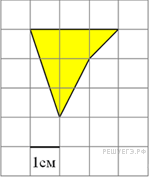 Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Решение.
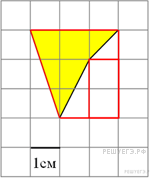 Площадь четырёхугольника равна разности площади трапеции, маленького прямоугольника и двух прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырёхугольника. Поэтому
Площадь четырёхугольника равна разности площади трапеции, маленького прямоугольника и двух прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырёхугольника. Поэтому
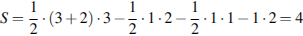 см2.
см2.
Примечание.
Данный четырёхугольник можно разбить на прямоугольный треугольник, с катетами 1 и 3, прямоугольную трапецию с основаниями 3 и 1 и прямоугольный треугольник с катетами 1 и 1. Поэтому его площадь равна 4.
№14. Площадь параллелограмма  равна 153. Найдите площадь параллелограмма
равна 153. Найдите площадь параллелограмма  , вершинами которого являются середины сторон данного параллелограмма.
, вершинами которого являются середины сторон данного параллелограмма.
Решение.
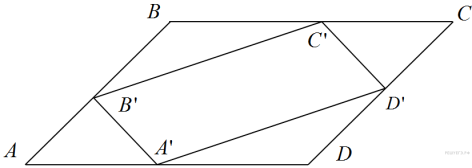
Четырехугольник, вершинами которого являются середины сторон произвольного четырехугольника, является параллелограммом, площадь которого равна половине площади исходного четырехугольника (см. параллелограмм Вариньона). Поэтому его площадь равна 76,5. Ответ:76,5.
№15. Площадь параллелограмма  равна 176. Точка
равна 176. Точка 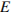 – середина стороны
– середина стороны  . Найдите площадь треугольника
. Найдите площадь треугольника 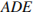 .
.
Решение.
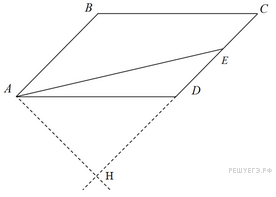
Пусть 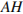 − перпендикуляр, опущенный из точки
− перпендикуляр, опущенный из точки 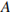 на продолжение стороны
на продолжение стороны 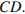 Выразим площадь треугольника
Выразим площадь треугольника 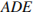 через площадь параллелограмма
через площадь параллелограмма 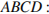
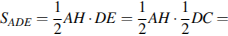
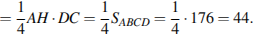 Ответ: 44.
Ответ: 44.
№16. Площадь треугольника ABC равна 12. DE ― средняя линия этого треугольника, параллельная стороне AB. Найдите площадь трапеции ABDE.
Решение.
Средняя линия отсекает треугольник, подобный исходному с коэффициентом 0,5. Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому площадь отсеченного треугольника вчетверо меньше: она равна 3. Тогда искомая площадь трапеции равна 12 − 3 = 9. Ответ: 9.
№17. Найдите площадь ромба, если его стороны равны 1, а один из углов равен 150°.
Решение.
Площадь ромба равна произведению квадрата его стороны и синуса его угла. Поэтому
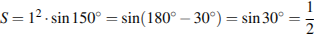 см2. Ответ: 0,5.
см2. Ответ: 0,5.
№18. Задание 4 № 27594. 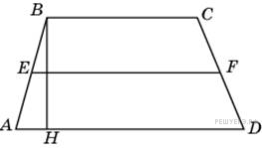 Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.
Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.
Решение.
Площадь трапеции равна произведению полусуммы оснований на высоту. Средняя линия трапеции равна полусумме оснований. Поэтому 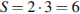 см2 Ответ: 6.
см2 Ответ: 6.
№19. 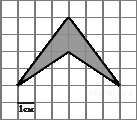 На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
Решение.
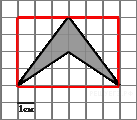 Площадь фигуры равна разности площади прямоугольника и трех треугольников. Поэтому
Площадь фигуры равна разности площади прямоугольника и трех треугольников. Поэтому
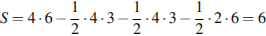 см2. Ответ: 6.
см2. Ответ: 6.
№20. 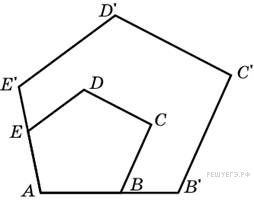 Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.
Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.
Решение.
Отношение площадей подобных многоугольников равно квадрату отношения их периметров. Пусть периметр и площадь меньшего многоугольника соответственно равны P 1 и S 1, периметр и площадь большего многоугольника соответственно равны P 2 и S 2. Поэтому
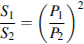 ,откуда
,откуда 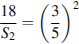 , Поэтому S 2 = 50. Ответ: 50.
, Поэтому S 2 = 50. Ответ: 50.
№21. 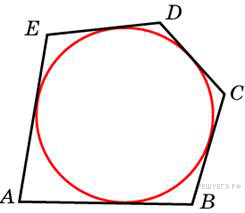 Около окружности, радиус которой равен 3, описан многоугольник, площадь которого равна 33. Найдите его периметр. Решение. Радиус вписанной в многоугольник окружности равен отношению его площади к полупериметру. Пусть площадь равна S, периметр равен P, радиус окружности равен R. Тогда
Около окружности, радиус которой равен 3, описан многоугольник, площадь которого равна 33. Найдите его периметр. Решение. Радиус вписанной в многоугольник окружности равен отношению его площади к полупериметру. Пусть площадь равна S, периметр равен P, радиус окружности равен R. Тогда 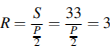 . Поэтому P = 22. Ответ: 22.
. Поэтому P = 22. Ответ: 22.
№22. 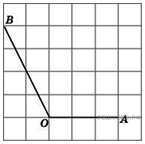 Найдите тангенс угла
Найдите тангенс угла  .
.
Решение.
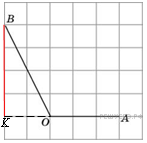 проведем высоту
проведем высоту 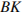 из точки
из точки 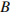 на продолжение стороны
на продолжение стороны 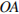 . Тогда:
. Тогда:
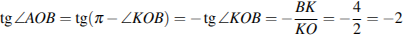 . Ответ: -2.
. Ответ: -2.
№23. 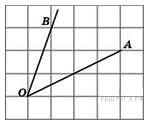 Найдите тангенс угла
Найдите тангенс угла  .
.
Решение.
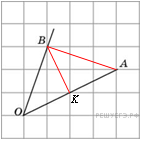 Достроим угол до треугольника
Достроим угол до треугольника  ,
, 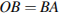 .
. 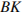 делит основание
делит основание 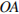 пополам, значит,
пополам, значит, 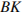 – высота. Из рисунка находим
– высота. Из рисунка находим 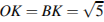 .
.
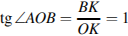 .
.
Примечание.
Можно заметить и доказать, что равнобедренный треугольник ABO является прямоугольным. Тогда углы AOB и OАB равны 45°, а их тангенсы равны 1. Ответ: 1.
№24.
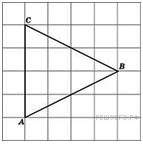 Найдите биссектрису треугольника
Найдите биссектрису треугольника 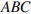 , проведенную из вершины
, проведенную из вершины  , если стороны квадратных клеток равны 1. Решение.
, если стороны квадратных клеток равны 1. Решение.
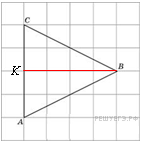 по рисунку видно, что
по рисунку видно, что  , значит, биссектриса, проведенная из вершины
, значит, биссектриса, проведенная из вершины  , также будет делить основание
, также будет делить основание 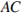 пополам. Построим отрезок
пополам. Построим отрезок 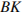 . Видно, что он равен 4. Ответ: 4.
. Видно, что он равен 4. Ответ: 4.
№25. 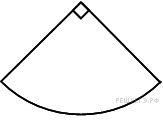 Найдите площадь сектора круга радиуса
Найдите площадь сектора круга радиуса 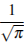 , центральный угол которого равен 90°.
, центральный угол которого равен 90°.
Решение. Площадь сектора круга, центральный угол которого равен 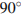 n° равна четверти площади круга. Поэтому
n° равна четверти площади круга. Поэтому
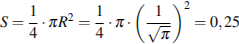 . Ответ: 0,25.
. Ответ: 0,25.
№26. 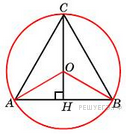 Высота правильного треугольника равна 3. Найдите радиус окружности, описанной около этого треугольника.
Высота правильного треугольника равна 3. Найдите радиус окружности, описанной около этого треугольника.
Решение. Треугольник 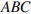 правильный, значит, все углы равны по
правильный, значит, все углы равны по 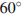 . По теореме синусов имеем:
. По теореме синусов имеем:
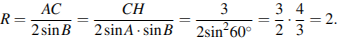 Ответ: 2.
Ответ: 2.
Приведём другое решение. В правильном треугольнике радиус описанной окружности равен двум третьим высоты. Поэтому он равен 2.
№27. 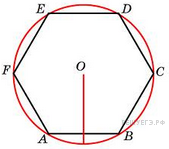 Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Решение.
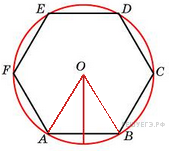
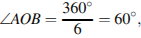
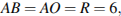 значит, треугольник
значит, треугольник 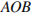 – равносторонний.
– равносторонний.
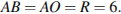 Ответ: 6.
Ответ: 6.
№28. 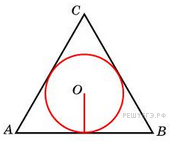 Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6. Решение. Радиус окружности, вписанной в равносторонний треугольник, равен одной трети высоты. Поэтому он равен 2. Ответ: 2.
Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6. Решение. Радиус окружности, вписанной в равносторонний треугольник, равен одной трети высоты. Поэтому он равен 2. Ответ: 2.
№29. 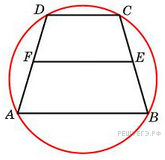 Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Решение. трапеция  – равнобедренная, т. к. вокруг неё описана окружность.
– равнобедренная, т. к. вокруг неё описана окружность.
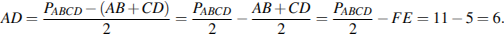 Ответ: 6.
Ответ: 6.
№30. На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры.

Решение.
Площади кругов относятся как квадраты их радиусов. Поскольку радиус большего круга равен четырем третьим радиуса меньшего круга, площадь большего круга составляет шестнадцать девятых площади меньшего. Следовательно, она равна 16. Площадь заштрихованной фигуры равна разности площадей кругов: 16 − 9 = 7. Ответ: 7.
№ 31. 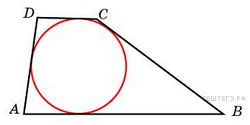 Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
Решение.
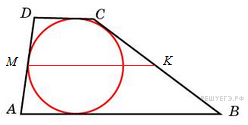
в выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда 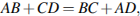
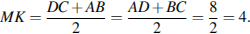 Ответ: 4.
Ответ: 4.
№32. Найдите длину вектора  (6; 8).
(6; 8).
Решение. Длина вектора определяется следующим выражением: 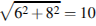 . Ответ: 10.
. Ответ: 10.
№33. 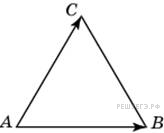 Стороны правильного треугольника
Стороны правильного треугольника  равны 3. Найдите длину вектора
равны 3. Найдите длину вектора 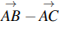 .
.
Решение. Разность 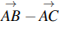 равна вектору
равна вектору 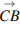 . Длина вектора
. Длина вектора 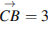 . Ответ: 3.
. Ответ: 3.
№34. 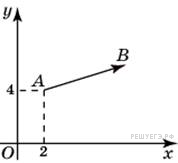 Вектор
Вектор 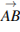 с началом в точке
с началом в точке 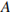 (2; 4) имеет координаты (6; 2). Найдите ординату точки
(2; 4) имеет координаты (6; 2). Найдите ординату точки 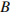 .
.
Решение. Координаты вектора равны разности координат конца вектора и его начала. Так как вектор 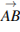 имеет координаты
имеет координаты 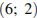 , то легко вычислить координаты точки
, то легко вычислить координаты точки 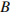 . Следовательно, точка
. Следовательно, точка 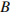 имеет координаты
имеет координаты 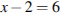 ,
, 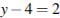 . Поэтому
. Поэтому 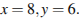 Ответ: 6.
Ответ: 6.
№35. 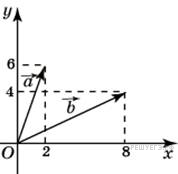 Найдите квадрат длины вектора
Найдите квадрат длины вектора  +
+ 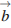 .
.
Решение.
Координаты суммы векторов равны суммам соответствующих координат: 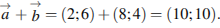 Тогда для длины вектора суммы имеем:
Тогда для длины вектора суммы имеем: 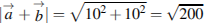 . Квадрат длины вектора равен 200. Ответ: 200.
. Квадрат длины вектора равен 200. Ответ: 200.
№36 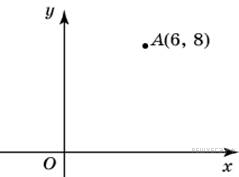 Через точку А (6; 8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью Oy.
Через точку А (6; 8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью Oy.
Решение. Ордината пересечения прямой с осью Oy совпадает с ординатой данной точки, то есть y = 8.
Ответ: 8.
 2015-04-12
2015-04-12 3125
3125






