Пример 15.1.
Вычислить интеграл 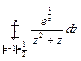 .
.
Решение. Контур 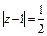 − окружность с центром в т.
− окружность с центром в т. 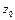 =1 и радиусом
=1 и радиусом 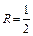 .
.
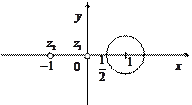
Рисунок 13.3
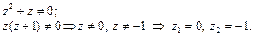
В точках 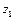 и
и 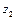 нарушается условие аналитичности функции т.к. полученные точки не попадают в область, ограниченной контуром
нарушается условие аналитичности функции т.к. полученные точки не попадают в область, ограниченной контуром 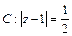 , то по теореме Коши
, то по теореме Коши 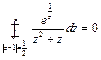 .
.
Пример 15.2.
Вычислить интеграл 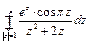 .
.
Решение. Внутри окружности 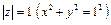 знаменатель дроби
знаменатель дроби 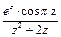 обращается в нуль в точке
обращается в нуль в точке 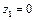 .
.
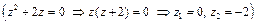
Для применения формулы (15.3) перепишем интеграл в следующем виде:
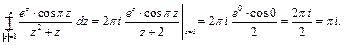
Пример 15.2.
Вычислить интеграл 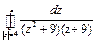 .
.
Решение. В области, ограниченной окружностью 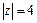 имеем две точки
имеем две точки 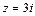 и
и 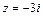 , в которых знаменатель подынтегральной функции
, в которых знаменатель подынтегральной функции 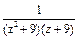 обращается в нуль:
обращается в нуль: 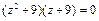 .
.
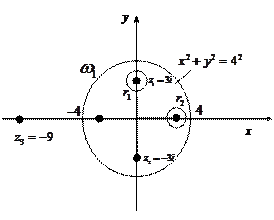
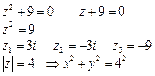
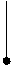
Рисунок 15.1
Непосредственно формулу (15.3) применять нельзя.
Построим окружности 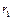 и
и 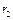 с центрами в точках
с центрами в точках 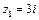 и
и 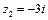 достаточно малых радиусов, таких, чтобы окружности не пересекались и целиком лежали в круге
достаточно малых радиусов, таких, чтобы окружности не пересекались и целиком лежали в круге 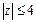 (рис.15.1).
(рис.15.1).
В трехсвязной области, ограниченной окружностями 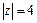 ,
, 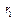 и
и 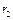 подыинтегральная функция всюду аналитична. По теореме Коши для многосвязной области:
подыинтегральная функция всюду аналитична. По теореме Коши для многосвязной области:
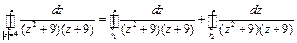 .
.
к каждому интегралу в правой части можно применить интегральную формулу Коши (15.3).
В результате получим:
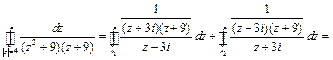
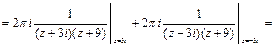
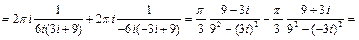
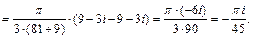
 2015-04-12
2015-04-12 146
146






