Модуль «Алгебра»

Комментарии к заданиям и критерии их оценивания

8 вариант

Часть 1

Каждое верно выполненное задание части 1 оценивается в 1 балл.

Модуль «Алгебра»	Модуль «Геометрия»
			-2		96,5	3,5					0,8

Модуль «Реальная математика»
			0,5		0,35

Часть 2

Модуль «Алгебра»

21. Решите систему уравнений .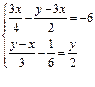

Решение. Домножив первое уравнение системы на 4, второе на 6, получаем 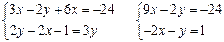, домножив второе уравнение системы на (-2) и сложив с первым находим 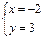Ответ: (-2; 3)

Баллы	Критерии оценки выполнения задания
	Задание решено верно
	Допущена вычислительная ошибка или описка, возможно, приведшая к неверному ответу
	Случаи, не соответствующие указанным крите­риям

22. На соревнованиях по кольцевой трассе один лыжник проходил круг на 3 мин быстрее другого и через час обогнал его ровно на круг. За сколько минут каждый лыжник проходил круг.

Решение. Пусть х мин – время прохождения круга одним лыжником, х>0(*). х+3 мин – время прохождения круга другим лыжником. 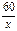- часть круга одним лыжником за 60 минут, 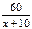- часть круга другим лыжником за 60 минут. Известно, что через час один отстал от другого на круг, имеем 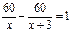. Решив это уравнение при условии (*), получаем х=12, тогда время другого 15 мин. Ответ: 12 мин и 15 мин

Баллы	Критерии оценки выполнения задания
	Задание решено верно
	При верных рассуждениях допущена вычислительная ошибка или описка, возможно, приведшая к неверному ответу
	Случаи, не соответствующие указанным крите­риям (не найдено время другого лыжника и т.д.)

23. Постройте график функции 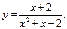Найдите все значения а, при которых график данной функции не имеет с прямой 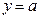общих точек.

Решение. В силу тождества 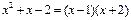, при всех значениях переменной, отличных от числа (-2), 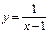. Тем самым, график функции представляет собой гиперболу с выколотой точкой

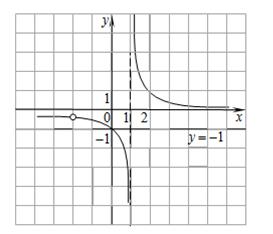
Из графика видно, что прямая 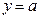не имеет с графиком функции общих точек пр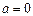и и 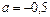. Ответ: см. рис.; 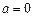и .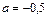

Баллы	Критерии оценки выполнения задания
	График построен верно, получен верныйответ
	График построен верно, ответ на вопрос не получен, получен неверно или не полностью
	Случаи, не соответствующие указанным кри­териям.

24. Углы В и А в треугольнике АВС равны 32° и 13°. Найдите сторону АВ, если радиус окружности, описанной около треугольника АВС равен, .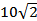

Решение:

Сумма углов в треугольнике равна 180°, значит, 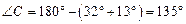. По следствию из теоремы синусов: 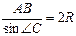, где R – радиус окружности, описанной около треугольника АВС.

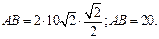Ответ: 20.

Баллы	Критерии оценки выполнения задания
	Получен верный обоснованный ответ.
	При верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу.
	Другие случаи, не соответствующие указанным критериям.

25. Точки М, N, K и L – середины сторон AB, BC, CD и DA прямоугольника . Докажите, что четырехугольник МNKL - ромб.

Доказательство: По свойству средней линии треугольника 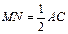, , 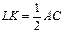, 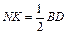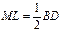.По свойству прямоугольника .

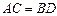Значит, МN = LK=NK=ML. Т.о. МNKL – ромб. Ч.т.д.

Баллы	Критерии оценки выполнения задания
	Доказательство верное, все шаги обоснованы
	Доказательство в целом верное, но содержит неточности
	Другие случаи, не соответствующие указанным критериям

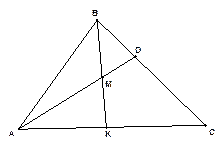26. Площадь треугольника АВС равна 120. Точка D лежит на отрезке ВС и делит его в отношении 1: 2, считая от вершины В. Биссектриса ВК пересекает отрезок AD в точке M, и делит сторону АС в отношении 3: 1, считая от вершины А. Найдите площадь четырехугольника MDCK.

Решение: 1) По условию задачи, 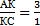. Треугольники

АВК и СВК имеют общую высоты, проведенную из вершины В, значит, 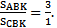Поэтому,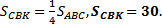

2) По условию задачи, 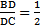. Треугольники АВD и СAD имеют общую высоту, проведенную из вершины A, значит, 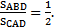Поэтому,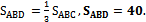

3) По свойству биссектрисы треугольника, 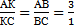. По условию, 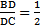, значит BC =3BD. Таким образом, 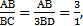значит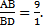

4) Рассмотрим треугольник ABD, ВМ – биссектриса, значит,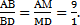

Тогда и 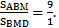Поэтому, 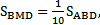таким образом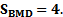

5) Тогда по свойству площади многоугольника, 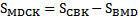, значит,

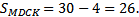Ответ: 26.

Баллы Критерии оценки выполнения задания   Ход решения верный, все его шаги выполнены правильно, получен верный ответ.   Ход решения верный, чертёж соответствует условию задачи, но, например, неверно составлены отношения площадей или допущена вычислительная ошибка.   Другие случаи, не соответствующие указанным критериям.