6.1–6.15. Найти массу, где 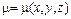 – плотность
– плотность
6.1. верхней половины кардиоиды 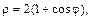 если
если 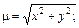
6.2. отрезка AB, где 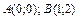 , если
, если 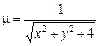 ;
;
6.3. отрезка АВ, где А (1,2); В (2,4), если плотность в каждой его точке равна произведению квадратов координат этой точки;
6.4. дуги лемнискаты 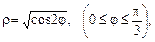 если
если 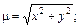
6.5. первой арки циклоиды 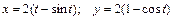 , если
, если 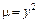 ;
;
6.6. дуги кривой 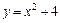 от точки А (0,4) до В (2,8), если плотность в каждой точке ее равна абсциссе точки;
от точки А (0,4) до В (2,8), если плотность в каждой точке ее равна абсциссе точки;
6.7. дуги окружности 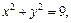 лежащей в первой четверти, если плотность в каждой ее точке равна абсциссе точки;
лежащей в первой четверти, если плотность в каждой ее точке равна абсциссе точки;
6.8. дуги кривой 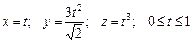 , если
, если 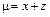 ;
;
6.9. дуги синусоиды 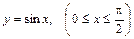 , если
, если 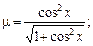
6.10. дуги окружности 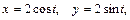 лежащей в первой четверти, если плотность ее в каждой точке равна произведению абсциссы на квадрат ординаты этой точки;
лежащей в первой четверти, если плотность ее в каждой точке равна произведению абсциссы на квадрат ординаты этой точки;
6.11. отрезка AB, где 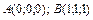 , если
, если 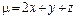 ;
;
6.12. дуги кривой 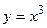 от точки А (1;1) до точки В (2;8), если плотность в каждой точке кривой равна ординате этой точки;
от точки А (1;1) до точки В (2;8), если плотность в каждой точке кривой равна ординате этой точки;
6.13. дуги тангенсоиды 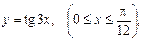 если
если 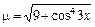 ;
;
6.14. правого лепестка лемнискаты 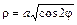 , если
, если 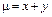 ;
;
6.15. одной арки циклоиды 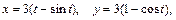 если плотность ее в каждой точке равна ординате точки.
если плотность ее в каждой точке равна ординате точки.
6.16–6.30. Вычислить работу силового поля 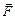 при перемещении материальной точки вдоль пути
при перемещении материальной точки вдоль пути 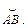
6.16. 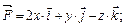
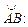
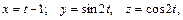
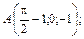 В
В 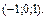
6.17. 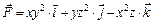 ,
, 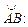 отрезок прямой,
отрезок прямой,
А (0;0;0); В (–2;4;5).
6.18. 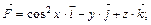
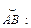
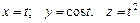 ,
,
А (0;1;0); В 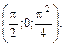
6.19. 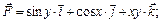
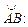
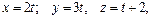
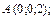 В
В 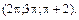
6.20. 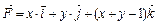 ,
, 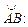 отрезок прямой,
отрезок прямой,
А (1;1;1); В (2;3;4).
6.21. 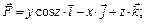
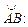 отрезок прямой,
отрезок прямой,
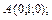 В
В 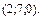
6.22. 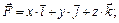
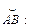
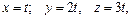
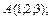 В
В 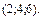
6.23. 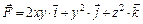 ,
, 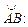
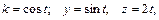
А (1;0;0); В (1;0;4π).
6.24. 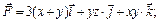
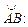 отрезок прямой,
отрезок прямой,
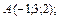 В
В 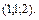
6.25. 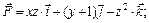
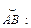
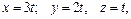
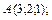 В
В 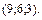
6.26. 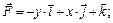
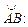
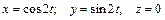
А (1;0;0); В (0;1;0).
6.27. 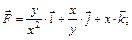
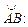 отрезок прямой,
отрезок прямой,
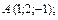 В
В 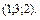
6.28. 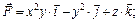
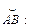
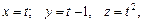
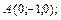 В
В 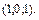
6.29. 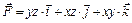 ;
; 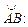 отрезок прямой,
отрезок прямой,
А (2;1;2); В (3;3;3).
6.30. 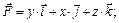
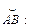
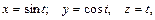
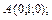 В
В 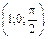
 2015-04-20
2015-04-20 1116
1116