2015-05-06
525Динамика-Д1
кинетического момента системы
Однородная горизонтальная платформа (круглая радиуса R или прямоугольная со сторонами R и 2R) вращается с угловой скоростью ω0 вокруг вертикальной оси z, отстоящей от центра масс С платформы на расстоянии ОС.
В момент времени t = 0 по желобу платформы начинает двигаться под действием внутренних сил груз D массой тD по закону s.
Одновременно на платформы начинает действовать пара сил с моментом М
(при М<0 его направление противоположно показанному на схемах).
Дано:
R = 2 м,
mплатф = 24 кг,
mплатф = 20 кг,
mгруз = 10 кг,
ω0=20 с-1,
ОС = см. таблицу,
s= AD = F(t) = см. таблицу,
М = см. таблицу.
Определить угловую скорость платформы ω как функцию времени.
На всех рисунках груз D показан в положении, при котором s>0.
При s<0 груз находится по другую сторону от точки А.
Номер варианта выбирается по двум последним цифрам зачетной книжки.
Предпоследняя цифра – вариант схемы.
Последняя цифра – номер условия.
Например: 091365, схема –6, условие – 5.
| Номер условия | b | s = F(t) | М |
| 0 | R | 16 t | -14 t3 |
| 1 | R | -0,8 t2 | 12 t2 |
| 2 | R | 0,4 t3 | -10t |
| 3 | R/2 | -t | 8 |
| 4 | R | 0,5 t2 | -4t3 |
| 5 | R/2 | -0,8 t3 | 12 t2 |
| 6 | R | 0,15 t | -10t |
| 7 | R | -0,9 t2 | 8 t3 |
| 8 | R | 3t3 | -6 t2 |
| 9 | R/2 | -0,7 t | 4 |
 
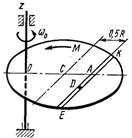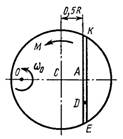Схема 0
|  
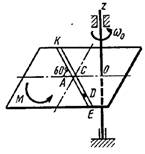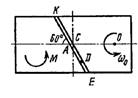Схема 1
|
 
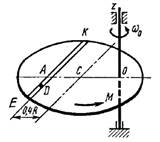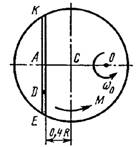Схема 2
|
 
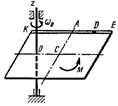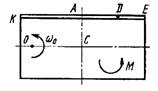Схема 3
|
 
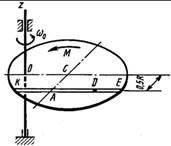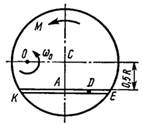Схема 4
|  
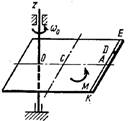Схема 5
|
 
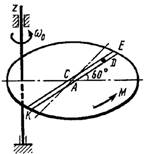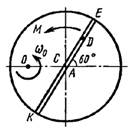Схема 6
|  
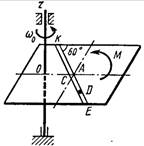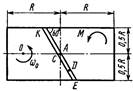Схема 7
|
 
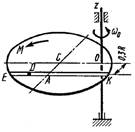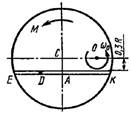Схема 8
|  
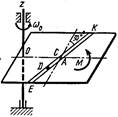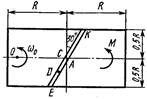Схема 9
|
