Скорость звука в воздухе (оценочный вывод формулы)

Рассмотрим процесс распространения звуковой волны в воздухе. В качестве источника звуковых волн возьмем колеблющуюся пластину. В результате смещения пластины у ее поверхности происходит увеличение давления 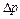и увеличение плотности на величину 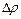. Сжатый воздух расширяется и вызывает сжатие прилегающего к нему слоя воздуха и т. д. При распространении волны сжатия масса 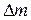воздуха, проходящего за время 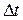через площадку S перпендикулярно направлению распространения волны, может быть выражена так,

,

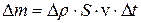где 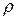- плотность воздуха и v-скорость распространения волны сжатия.

Запишем для массы воздуха 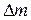закон изменения импульса

.

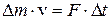Подставляя в этот закон выражение для 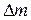и силы, действующей на эту массу 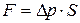, получим:

.

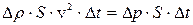Отсюда получим выражение для скорости распространения волны:

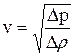или более строго .

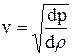Величина 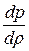зависит от условий, при которых происходит сжатие и расширение при распространении волны. В случае воздушной среды, теплопроводность которой мала, зоны сжатия и расширения в тепловом отношении оказываются практически изолированными и не обмениваются теплом, поэтому процесс можно считать адиабатическим. Для адиабатического процесса давление и объем связаны уравнением 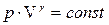, где 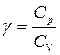, 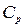-молярная теплоемкость газа при постоянном давлении, 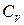- молярная теплоемкость газа при постоянном объеме. Выразив V через массу и плотность 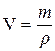, подставим его в уравнение адиабаты, получим: 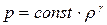, следовательно 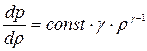или 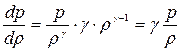. Таким образом выражение для скорости звука примет следующий вид:

_.

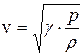Эту формулу удобно преобразовать к более удобному для расчета виду с использованием уравнения Менделеева-Клапейрона 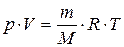или 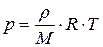. Подставляя выражение для давления в формулу для скорости звука, получим:

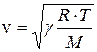. (6)

Преобразуя формулу (6), найдем:

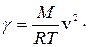(7)

Таким образом для определения показателя адиабаты надо знать температуру воздуха T и измерить скорость распространения звука v (молярная масса воздуха M=0,029 кг/моль).