СДНФ легко строится по таблице истинности, но если функция заданна формулой, ее СДНФ можно получить, преобразуя формулу, без построения таблицы истинности.
Построение СДНФ осуществляется в два этапа. Сначала строится ДНФ. А затем ДНФ превращается в СДНФ. Чтобы превратить формулу в ДНФ, нужно выполнить следующие действия.
1. Преобразовать формулу так, чтобы в ней остались только операции 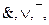 причем отрицания должны стоять только над отдельными аргументами. Для этого нужно воспользоваться законами де Моргана и равносильностями
причем отрицания должны стоять только над отдельными аргументами. Для этого нужно воспользоваться законами де Моргана и равносильностями 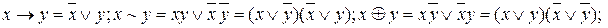
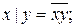
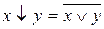 , которые доказываются по таблицам истинности.
, которые доказываются по таблицам истинности.
2. Раскрыть скобки и привести подобные, пользуясь законами дистрибутивности и другими равносильностями, а затем упростить формулу. В результате будет построена ДНФ.
3. Преобразовать ДНФ в СДНФ. Все ПЭК нужно превратить в полные ПЭК, для чего поступить так. Если в ПЭК не входит, например, переменная y, нужно домножить эту ПЭК на скобку 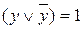 и раскрыть скобки. Повторить операцию столько раз, сколько нужно, чтобы все ПЭК стали полными. Если появятся одинаковые конъюнкции, нужно убрать повторения, ведь
и раскрыть скобки. Повторить операцию столько раз, сколько нужно, чтобы все ПЭК стали полными. Если появятся одинаковые конъюнкции, нужно убрать повторения, ведь 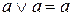 .
.
Пример. Построить СДНФ формулы 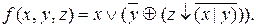
Сначала построим таблицу истинности этой формулы (табл. 3), а затем преобразуем формулу в СДНФ
Таблица 3
| x | y | z | 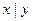 | 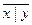 | 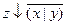 | 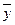 | 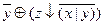 | 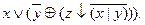 |
Эта функция равна 1 на шести наборах значений переменных, ее СДНФ содержит шесть слагаемых и такова
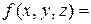
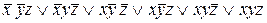 .
.
Преобразуем формулу
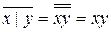 ;
; 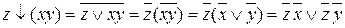 ;
;
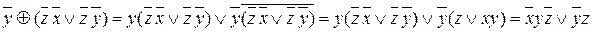 ;
;
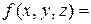
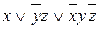 . Преобразуем ДНФ в СДНФ
. Преобразуем ДНФ в СДНФ
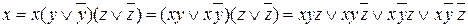 ;
;
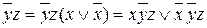 ;
; 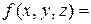
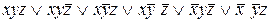 .
.
 2015-04-20
2015-04-20 2297
2297
