1. Функция F(x) называется первообразной функции f (x) на интервале (а,b), если для любого 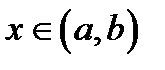 выполняется равенство
выполняется равенство
А) 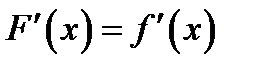
Б) 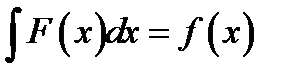
*В) 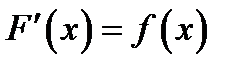
Г) 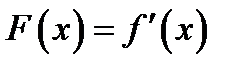
2.Дифференциал от неопределенного интеграла равен 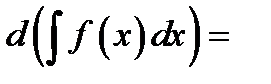
А) 
*Б)  dx
dx
В) 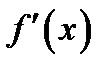
Г) 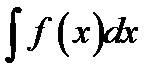
3. Производная неопределенного интеграла равна 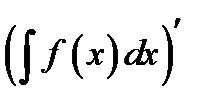
*А) 
Б)  dx
dx
В) 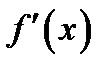
Г) 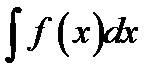
4. Неопределенный интеграл от дифференциала некоторой функции равен 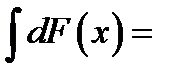
А) 
Б)  dx
dx
В) 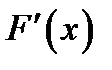
*Г) 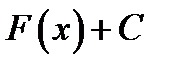
5. Пусть а- постоянная величина тогда 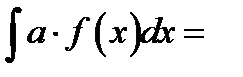
А) 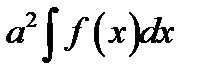
Б) 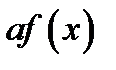
*В) 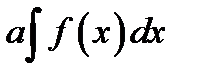
Г) 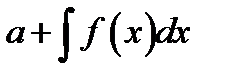
6. 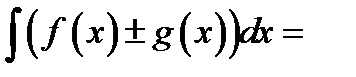
А) 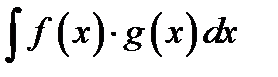
*Б) 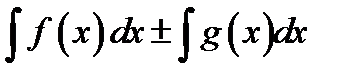
В) 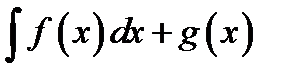
Г) 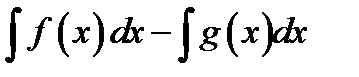
7. Формула интегрирования по частям имеет вид:
*А) 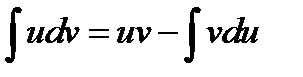
Б) 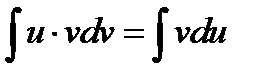
В) 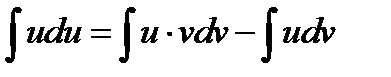
Г) 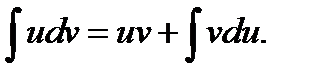
8. Пусть требуется вычислить интеграл 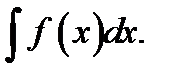 Сделаем подстановку
Сделаем подстановку 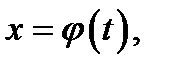 где
где 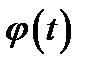 - функция, имеющая непрерывную производную. Тогда формула замены переменных в неопределенном интеграле имеет вид:
- функция, имеющая непрерывную производную. Тогда формула замены переменных в неопределенном интеграле имеет вид:
А) 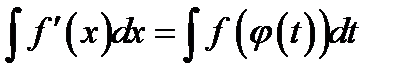
Б) 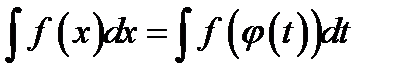
В) 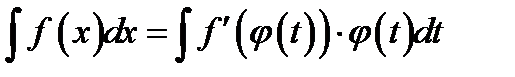
*Г) 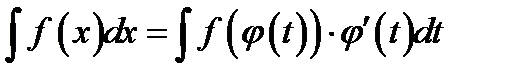
9. Функция вида: 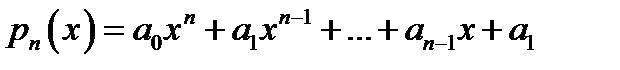 , где n – натуральное число,
, где n – натуральное число, 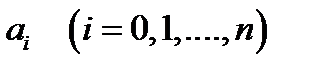 - постоянные коэффициенты, называется
- постоянные коэффициенты, называется
*А) целой рациональной функцией;
Б) дробно-рациональной функцией
В) иррациональной функцией
Г) рациональной дробью
10. Корнем многочлена 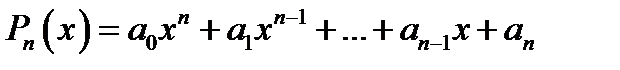 называется такое значение x0 переменной x, при котором
называется такое значение x0 переменной x, при котором
*А) 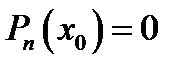
Б) 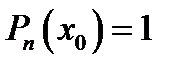
В) 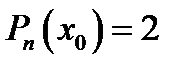
Г) 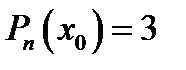
11. Если x 1, x 2,….. x n- корни многочлена P n(x), а 0 – коэффициент многочлена при x n, то многочлен P n(x) можно представить в виде:
А) P n(x0) = 0
*Б) P n(x) = а 0 (x – x 1)(x – x 2)…….(x - x n)
В) P n(x) = а 0 (x + x 1)(x + x 2)…….(x + x n)
Г) P n(x) = (x - x 1)(x - x 2)…….(x - x n)
12. Если x 1 – корень многочлена P n(x) кратности k1, x 2 – кратности k2, …, корень xr имеет кратность kr, при этом k1 + k2 +….+ kr = n, а 0 – коэффициент при x n разложение многочлена P n(x) можно записать в виде:
А) P n(x) = а 0 (x + x 1)(x + x 2)…….(x + x r)
Б) P n(x) = (x - x 1)(x - x 2)…….(x - x r)
*В) P n(x) = а 0 (x – x 1) 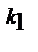 (x – x 2)
(x – x 2) 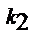 …….(x - x n)
…….(x - x n) 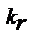
Г) P n(x) = а 0 (x + x 1) 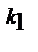 (x + x 2)
(x + x 2) 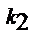 …….(x + x n)
…….(x + x n) 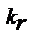
13. Рациональная дробь называется правильной, если
А) степень числителя равна степени знаменателя
*Б) степень числителя меньше степени знаменателя
В) степень числителя больше степени знаменателя
Г) степень числителя и степени знаменателя равны единице
14. 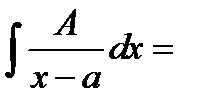
*А) 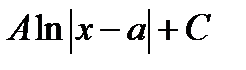
Б) 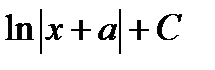
В) 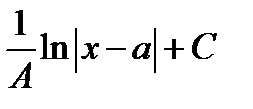
Г) 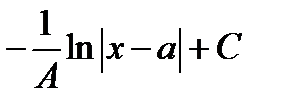
15. 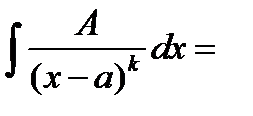
А) 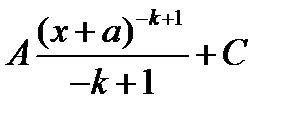
Б) 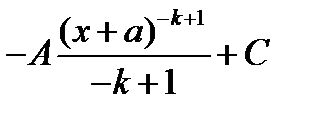
В) 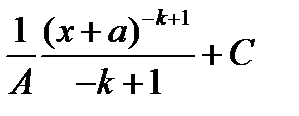
*Г) 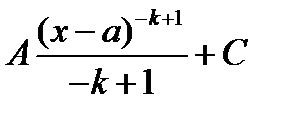
16. Непрерывная функция имеет
А) только одну первообразную
*Б) бесконечное множество первообразных
В) две первообразных
17. Две различные первообразные одной и той же функции
А) равны между собой
*Б) отличаются на константу
В) отличаются на некоторую функцию
18. К интегрируемым функциям относятся все
А) постоянные
*Б) непрерывные
В) прерывные
19. Совокупность всех первообразных 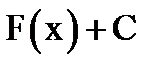 от функции f(x) называется
от функции f(x) называется
А) дифференциалом 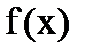
Б) определенным интегралом
*В) неопределенным интегралом
20. Проверить соответствие формул:
1) 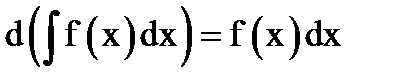 ; 2)
; 2) 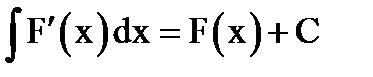 ; 3)
; 3) 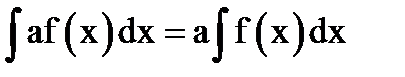
*А) верно
Б) ошибка в 2)
В) ошибка в 3)
21. 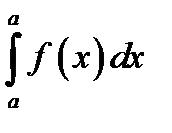 равен
равен
А) -1
Б) 1
*В) 0
Г) а
22. для любого действительного числа С 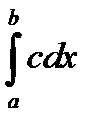 равен
равен
*А) c (b-a)
Б) c (b+a)
В) - c (b-a)
Г) 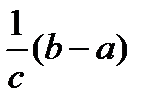
23. Если функция y = f (x) непрерывна на отрезке 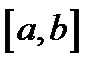 и F (x) – какая либо ее первообразная на
и F (x) – какая либо ее первообразная на 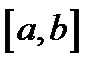
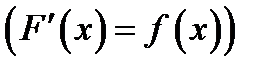 , то формула Ньютона-Лейбница имеет вид:
, то формула Ньютона-Лейбница имеет вид:
А) 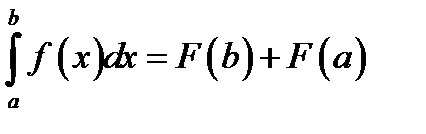
Б) 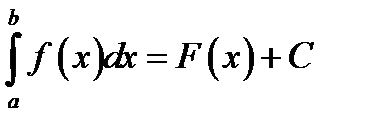
*В) 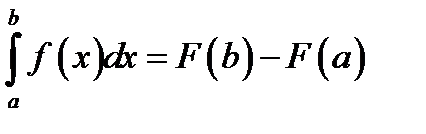
Г) 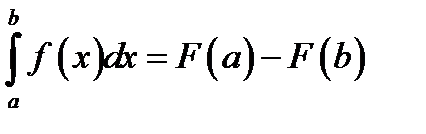
24.Если с – постоянное число и функция f (x) итегрируема на 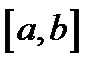 , то
, то
*А) 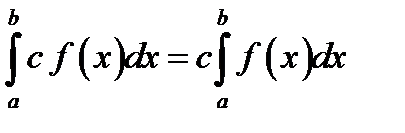
Б) 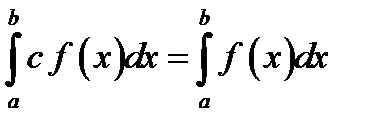
В) 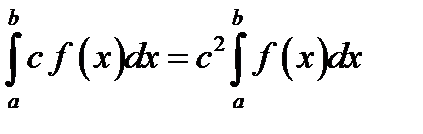
Г) 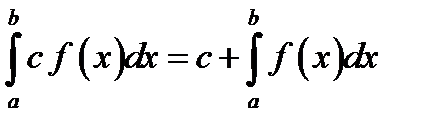
25. Если функция f (x) итегрируема на 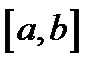 и a < c < b, то
и a < c < b, то
А) 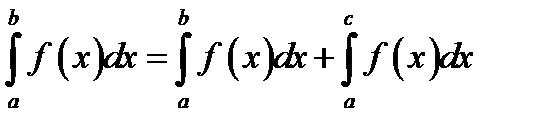
Б) 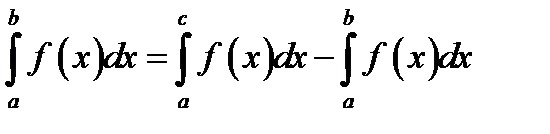
*В) 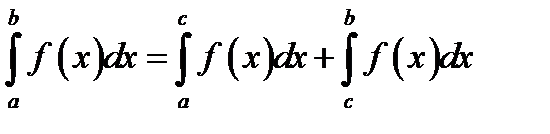
Г) 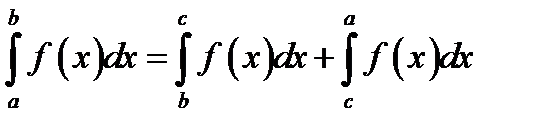
26. Если функция f (x) непрерывна на отрезке 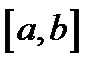 , то существует точка
, то существует точка 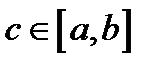 такая, что
такая, что
А) 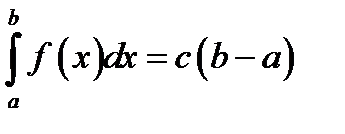
Б) 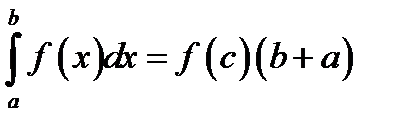
*В) 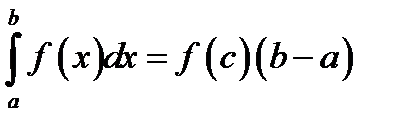
Г) 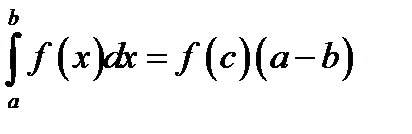
27. Если функции f1 (x) и f2 (x) непрерывные на отрезке 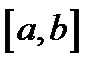 функции, и
функции, и 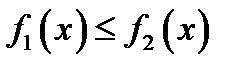 при
при 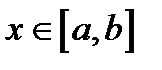 , то
, то
А) 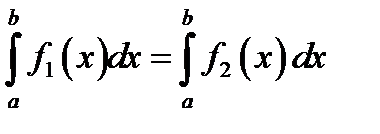
Б) 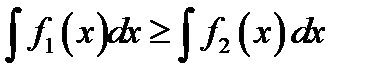
В) 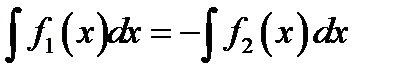
*Г) 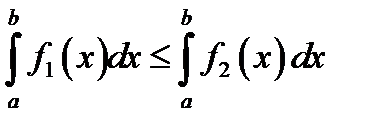
28. Если m и М – соответственно наименьшее и наибольшее значения функции y = f (x) на отрезке 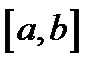 , (a < b), то
, (a < b), то
*А) 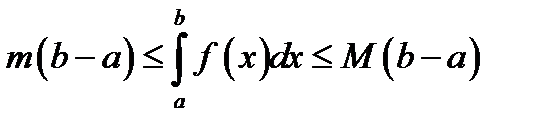
Б) 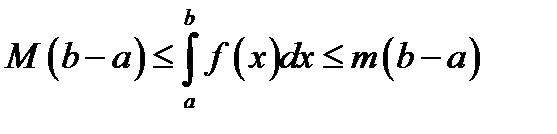
В) 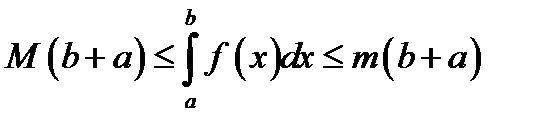
Г) 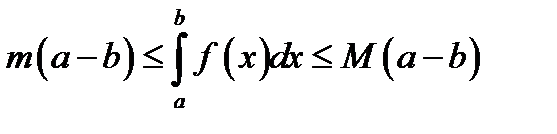
29. Площадь фигуры, ограниченной кривыми y = f1 (x) и y = f2 (x), прямыми
x = a и x = b при условии 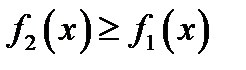 , можно найти по формуле
, можно найти по формуле
А) 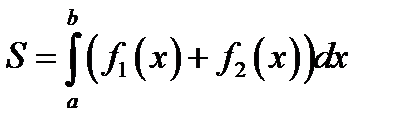
*Б) 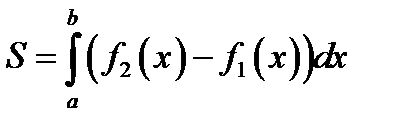
В) 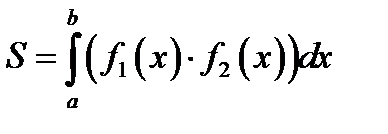
Г) 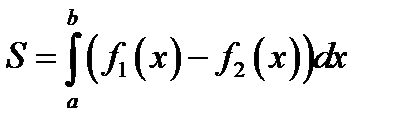
30. В выражении 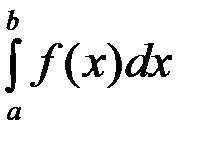 функция
функция 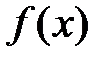 называется
называется
А) подынтегральным выражением
Б) интегральной суммой
*В) подынтегральной функцией
31. Если непрерывные функции удовлетворяют неравенству 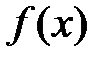 ≤
≤ 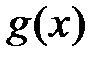 при
при 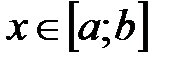 , то
, то
А) 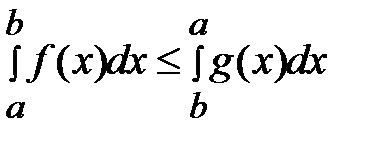
Б) 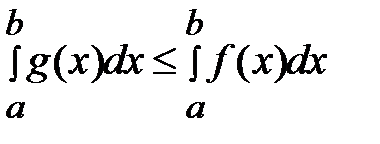
*В) 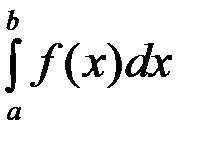 ≤
≤ 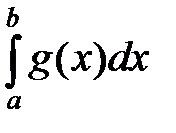
32. Функция 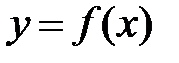 интегрируема на отрезке
интегрируема на отрезке 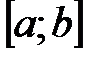 , если она на этом отрезке:
, если она на этом отрезке:
*А) непрерывна
Б) монотонна
В) неотрицательна
33. В формуле интегрирования по частям для определенного интеграла 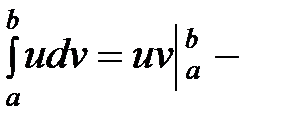
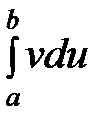 функции
функции 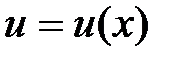 и
и 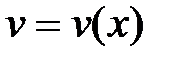 на отрезке
на отрезке 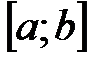 :
:
*А) имеют непрерывные производные
Б) неположительны
В) постоянны
34. Площадь криволинейного сектора, т.е. плоской фигуры, ограниченной непрерывной линией 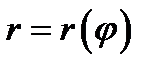 и двумя лучами
и двумя лучами 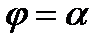 и
и 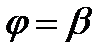
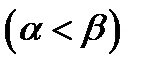 , где r и
, где r и 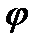 - полярные координаты, вычисляется по формуле:
- полярные координаты, вычисляется по формуле:
А) 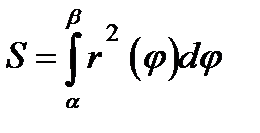
Б) 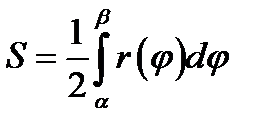
В) 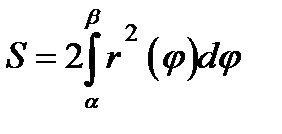
*Г) 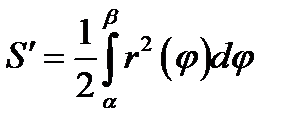
35. Пусть в прямоугольных координатах дана плоская кривая AB, уравнение которой y = f (x), где  . Если функция y = f (x) и ее производная
. Если функция y = f (x) и ее производная 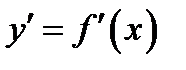 непрерывны на отрезке
непрерывны на отрезке 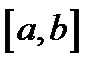 , то кривая AB имеет длину равную
, то кривая AB имеет длину равную
*А) 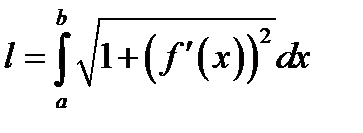
Б) 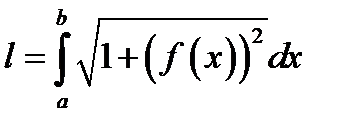
В) 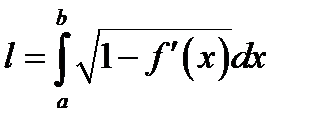
Г) 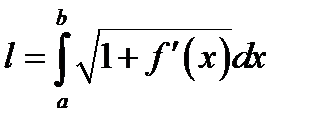
36. Если уравнение кривой AB задано в параметрической форме 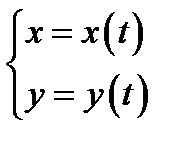 ,
, 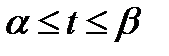 , где x (t) и y (t) – непрерывные функции с непрерывными производными и
, где x (t) и y (t) – непрерывные функции с непрерывными производными и 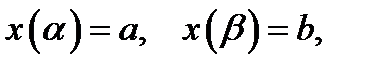 то длина
то длина 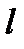 кривой AB находится по формуле
кривой AB находится по формуле
А) 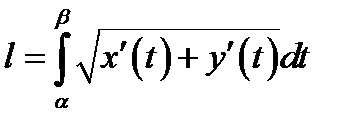
Б) 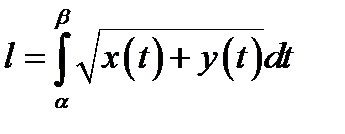
*В) 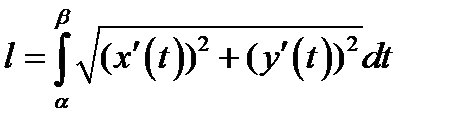
Г) 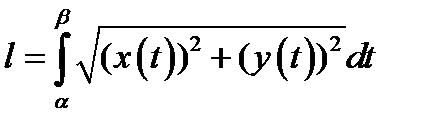
37. Частная производная по х от функции 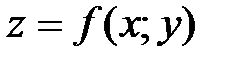 определяется равенством:
определяется равенством:
*А) 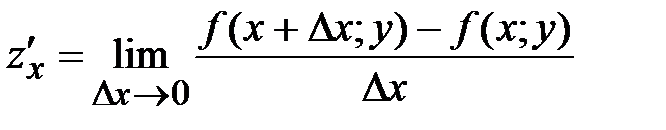
Б) 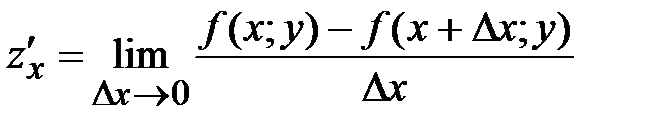
В) 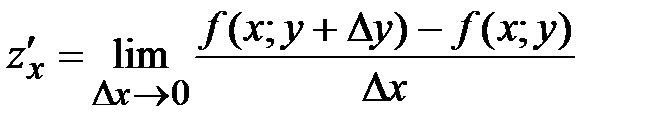
38. Частная производная по y от функции 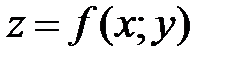 определяется равенством:
определяется равенством:
*А) 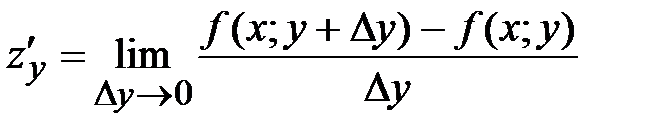
Б) 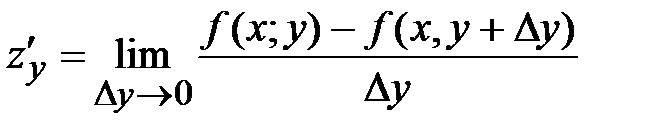
В) 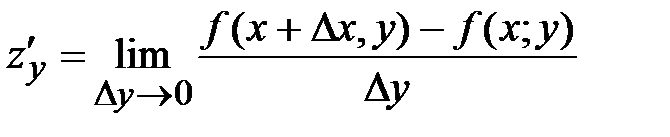
39. Формула для вычисления приближенных значений имеет вид:
А) 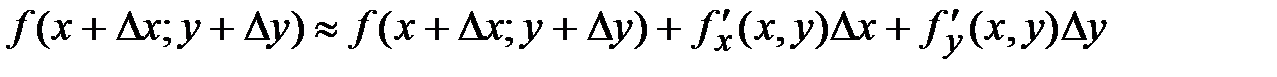
Б) 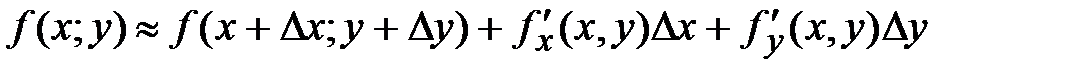
*В) 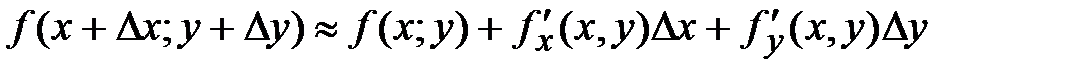
40. Точка (х0;у0) называется точкой максимумафункции 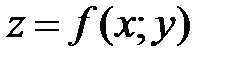 , если существует такая
, если существует такая 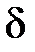 - окрестность точки (х0;у0), что для каждой точки (х, у), отличной от (х0;у0), из этой окрестности выполняется неравенство:
- окрестность точки (х0;у0), что для каждой точки (х, у), отличной от (х0;у0), из этой окрестности выполняется неравенство:
А) 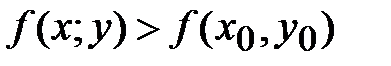
*Б) 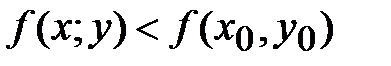
В) 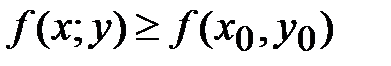
41. Точка (х0;у0) называется точкой минимумафункции 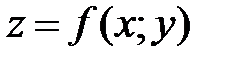 , если существует такая
, если существует такая 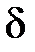 -окрестность точки (х0;у0), что для каждой точки (х; у), отличной от (х0;у0), из этой окрестности выполняется неравенство:
-окрестность точки (х0;у0), что для каждой точки (х; у), отличной от (х0;у0), из этой окрестности выполняется неравенство:
*А) 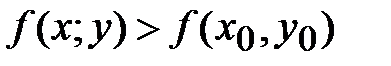
Б) 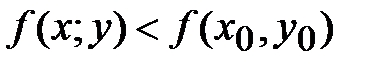
В) 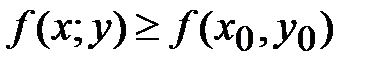
42. Если в точке N(х0;у0) дифференцируемая функция 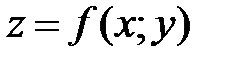 имеет экстремум, то ее частные производные в этой точке:
имеет экстремум, то ее частные производные в этой точке:
*А) 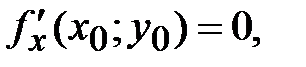
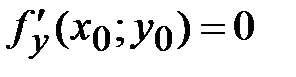
Б) 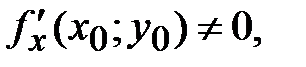
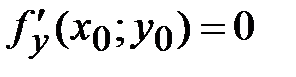
В) 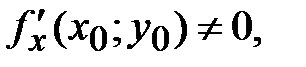
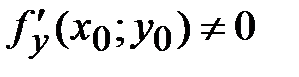
43. Производная по направлению  от функции
от функции 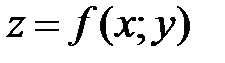 определяется равенством:
определяется равенством:
*А) 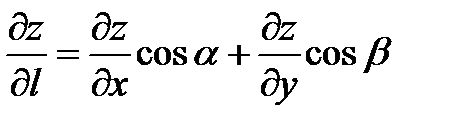
Б) 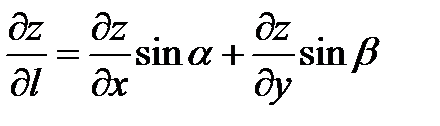
В) 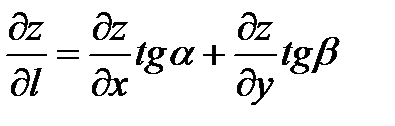
44. Градиентом функции 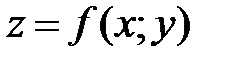 называется вектор с координатами:
называется вектор с координатами:
*А) 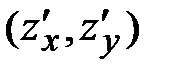
Б) 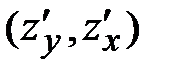
В) (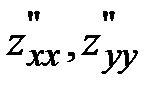 )
)
45. Функция Лагранжа имеет вид:
*А) 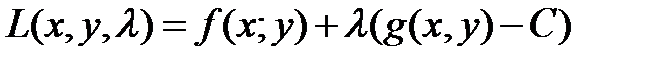
Б) 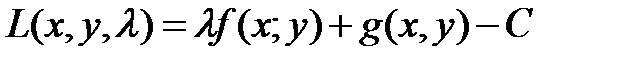
В) 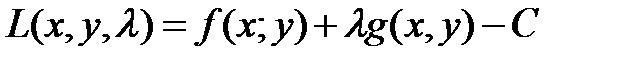
46. Производной функции 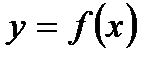 в точке х0 называется
в точке х0 называется
*А) 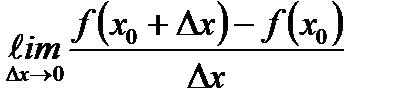
Б) 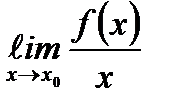
В) 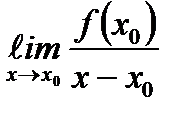

Г) 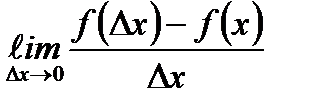
47. Уравнение касательной к графику функции 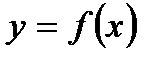 в точке
в точке 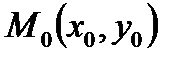 имеет вид:
имеет вид:
*А) 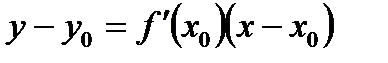
Б) 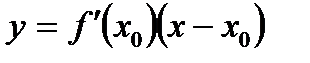
В) 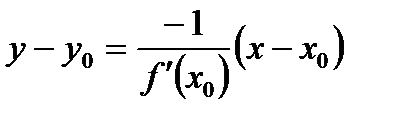
Г) 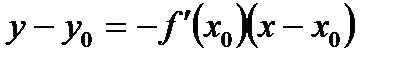
48. Уравнение нормали к графику функции 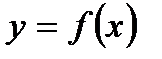 в точке
в точке 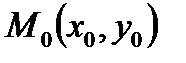 имеет вид:
имеет вид:
А) 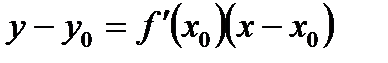
Б) 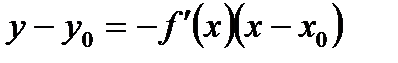
В) 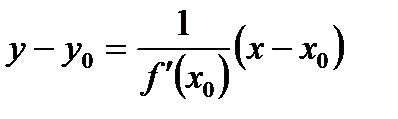
*Г) 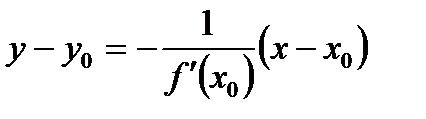
49. Функция 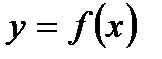 называется гладкой в некотором интервале
называется гладкой в некотором интервале 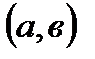 , если
, если
А) непрерывна в этом интервале
Б) имеет непрерывную производную в этом интервале
*В) монотонна в этом интервале
Г) не имеет производной в этом интервале
50. Теорема Роля гласит: если функция 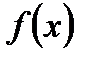 непрерывна на отрезке
непрерывна на отрезке 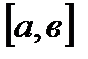 дифференцируема на интервале
дифференцируема на интервале 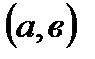 и на концах отрезка принимает одинаковое значения
и на концах отрезка принимает одинаковое значения 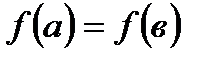 , то найдется хотя бы одна точка
, то найдется хотя бы одна точка 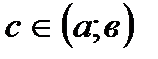 , в которой:
, в которой:
А) 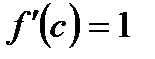
*Б) 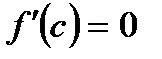
В) 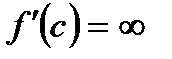
Г) 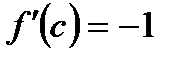
51. Теорема Коши гласит: если функции 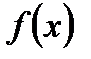 и
и 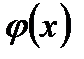 непрерывны на отрезке
непрерывны на отрезке 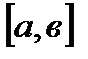 дифференцируемы на интервале
дифференцируемы на интервале 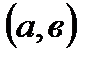 причем
причем 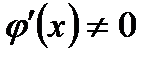 для
для 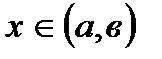 , то найдется хотя бы одна точка
, то найдется хотя бы одна точка 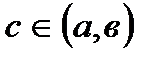 , что выполняется равенство:
, что выполняется равенство:
*А) 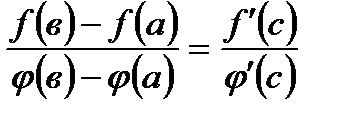
Б) 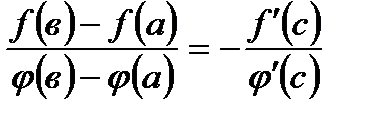
В) 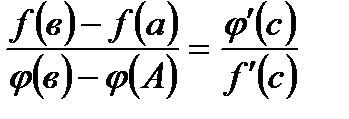
Г) 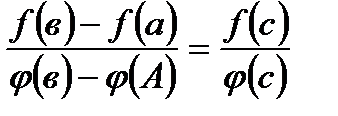
52. Теорема Лагранжа гласит: если функция 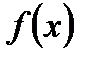 непрерывна на отрезке
непрерывна на отрезке 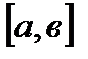 , дифференцируема на интервале
, дифференцируема на интервале 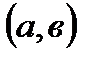 , то найдется хотя бы одна точка
, то найдется хотя бы одна точка 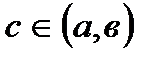 , такая, что выполняется равенство:
, такая, что выполняется равенство:
А) 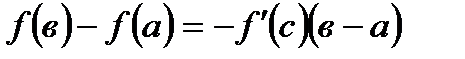
Б) 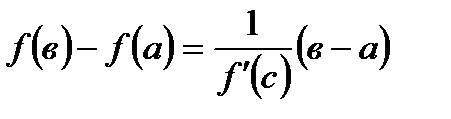
В) 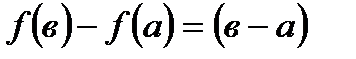
*Г) 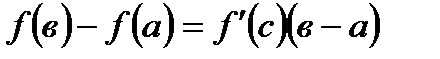
53. Если дифференцируемая на интервале 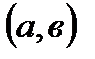 функция
функция 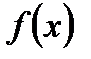 возрастает,
возрастает,
А) 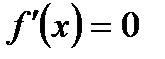
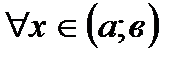
*Б) 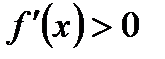
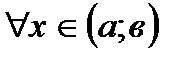
В) 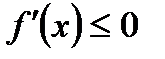
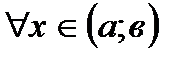
Г) 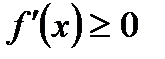
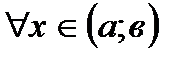
54. Если дифференцируемая на интервале 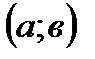 функция
функция 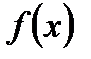 убывает, то:
убывает, то:
А) 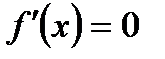
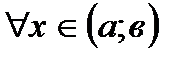
*Б) 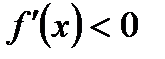
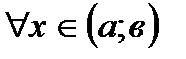
В) 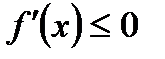
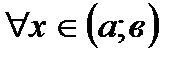
Г) 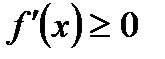
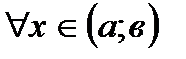
55. Точка 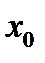 называется точкой максимума функции
называется точкой максимума функции 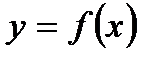 , если существует такая
, если существует такая 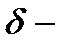 окрестность точки
окрестность точки 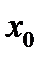 , что для всех
, что для всех 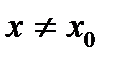 из этой окрестности выполняется неравенство:
из этой окрестности выполняется неравенство:
* А) 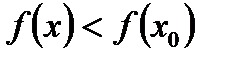
Б) 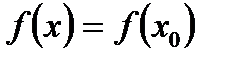
В) 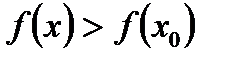
Г) 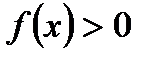
56. Точка 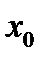 называется точкой минимума функции
называется точкой минимума функции 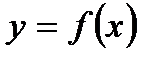 , если существует такая
, если существует такая 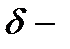 окрестность точки
окрестность точки 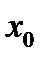 , что для всех
, что для всех 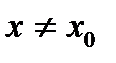 из этой окрестности выполняется неравенство:
из этой окрестности выполняется неравенство:
А) 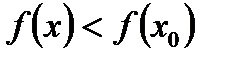
Б) 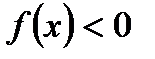
*В) 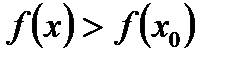
Г) 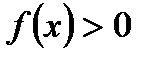
57. Если дифференцируемая функция 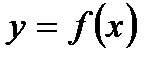 имеет экстремум в точке
имеет экстремум в точке 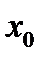 , то:
, то:
А) 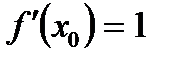
*Б) 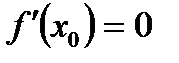
В) 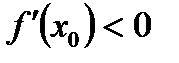
Г) 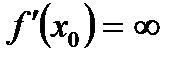
58. Если дифференцируемая функция 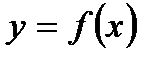 имеет максимум в точке
имеет максимум в точке 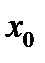 , то:
, то:
*А) 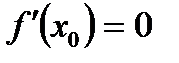 , а
, а 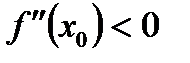
Б) 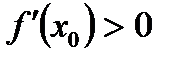 , а
, а 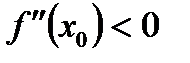
В) 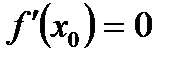 , а
, а 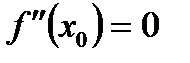
Г) 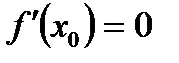 , а
, а 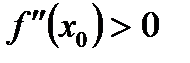
59. Если дифференцируемая функция 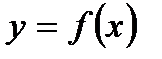 имеет минимум в точке
имеет минимум в точке 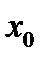 , то:
, то:
А) 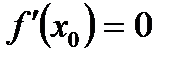 , а
, а 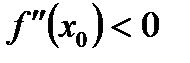
Б) 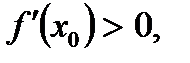 а
а 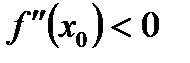
В) 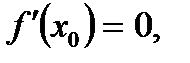 а
а 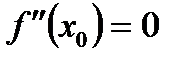
* Г) 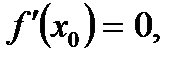 а
а 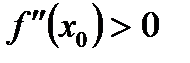
60. Функция 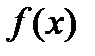 называется неубывающей на множестве х
называется неубывающей на множестве х 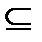 Д(f), если для любых значений х1, х2
Д(f), если для любых значений х1, х2 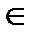 Х таких, что х1< х2, справедливо неравенство
Х таких, что х1< х2, справедливо неравенство
А) 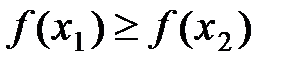
*Б) 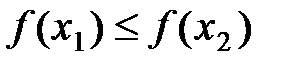
В) 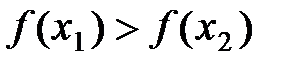
Г) 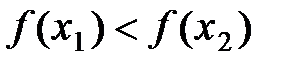
61. Функция 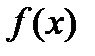 называется невозрастающей на множестве
называется невозрастающей на множестве 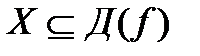 , если для любых значений
, если для любых значений 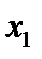 ,
, 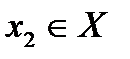 таких, что
таких, что 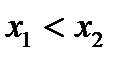 , справедливо неравенство:
, справедливо неравенство:
*А) 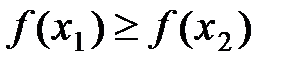
Б) 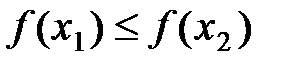
В) 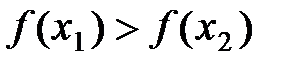
Г) 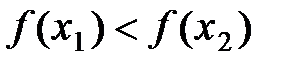
62. Функция 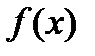 называется возрастающей на множестве
называется возрастающей на множестве 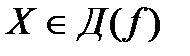 , если для любых значений
, если для любых значений 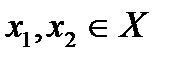 таких, что
таких, что 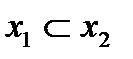 , справедливо неравенство:
, справедливо неравенство:
А) 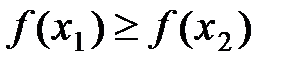
Б) 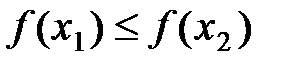
В) 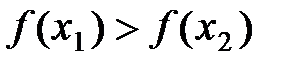
* Г) 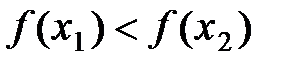
63. Функция 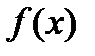 называется убывающей на множестве
называется убывающей на множестве 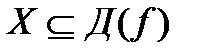 , если для любых значений
, если для любых значений 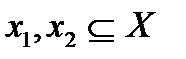 таких, что
таких, что 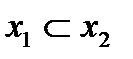 , справедливо неравенство:
, справедливо неравенство:
А) 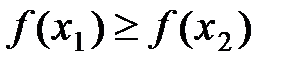
Б) 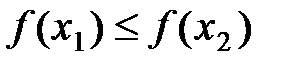
*В) 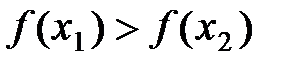
Г) 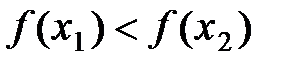
64. Функция 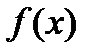 называется строго монотонной, если она:
называется строго монотонной, если она:
А) возрастающая или невозрастающая;
*Б) возрастающая или убывающая;
В) невозрастающая или неубывающая;
Г) невозрастающая или убывающая.
65. Функция 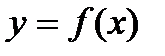 называется ограниченной на множестве
называется ограниченной на множестве 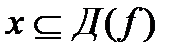 , если:
, если:
А) существует число 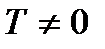 , что
, что 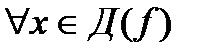
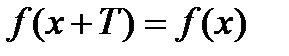 ;
;
*Б) существует такое число 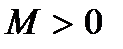 , что
, что 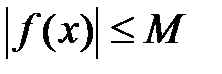
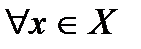 ;
;
В) 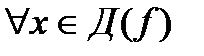 справедливо равенство
справедливо равенство 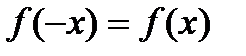 ;
;
Г) 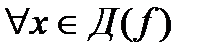 справедливо равенство
справедливо равенство 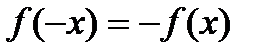 .
.
66. Функция 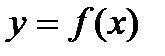 называется периодической на множестве
называется периодической на множестве 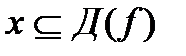 , если:
, если:
*А) существует число 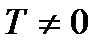 , что
, что 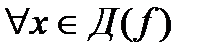
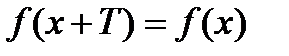 ;
;
Б) существует такое число М >0, что 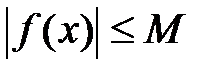
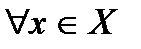 ;
;
В) 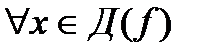 справедливо равенство
справедливо равенство 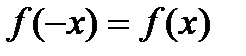 ;
; 
Г) 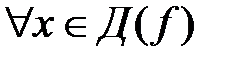 справедливо равенство
справедливо равенство 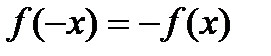 ;
;
67. График функции 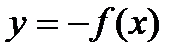 получается из графика функции
получается из графика функции 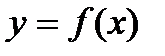 симметричным отражением относительно:
симметричным отражением относительно:
*А) оси 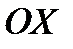 ;
;
Б) прямой 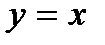 ;
;
В) прямой 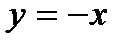 ;
;
Г) оси 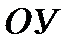 .
.
68. График функции 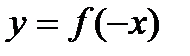 получается из графика функции
получается из графика функции 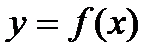 симметричным отражением относительно:
симметричным отражением относительно:
А) оси 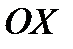 ;
;
Б) прямой 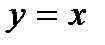 ;
;
В) прямой 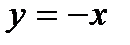 ;
;
* Г) оси 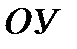 .
.
69. Если к- произвольное число и функция 
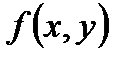 интегрируема в области Д, то функция
интегрируема в области Д, то функция 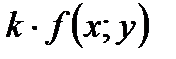 также интегрируема и
также интегрируема и
А) 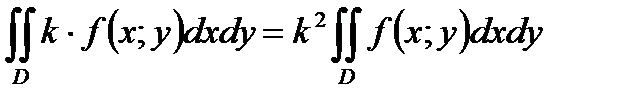
*Б) 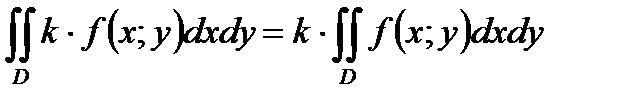
В) 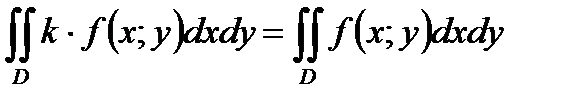
Г) 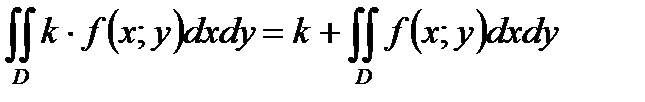
70. Если функции 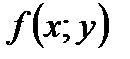 и
и 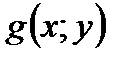 интегрируемы в области
интегрируемы в области 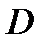 , то их алгебраическая сумма также интегрируема в этой области и
, то их алгебраическая сумма также интегрируема в этой области и 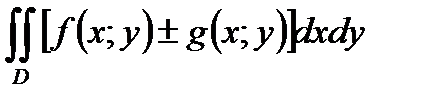 равен
равен
А) 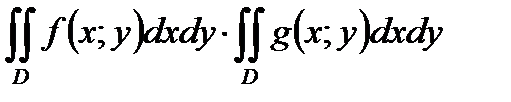
*Б) 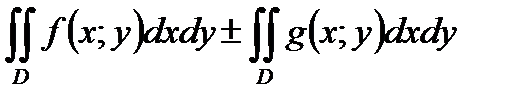
В) 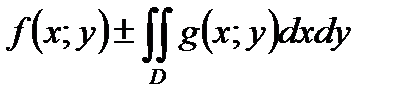
Г) 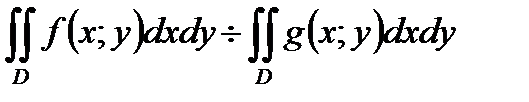
71. Если область 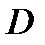 является объединением областей
является объединением областей 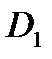 и
и 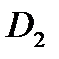 не имеющих общих внутренних точек, в каждой из которых функция
не имеющих общих внутренних точек, в каждой из которых функция 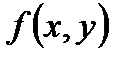 интегрируема, то в области
интегрируема, то в области 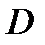 эта функция также интегрируема и
эта функция также интегрируема и 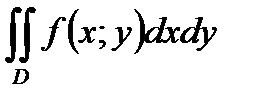 равен:
равен:
А) 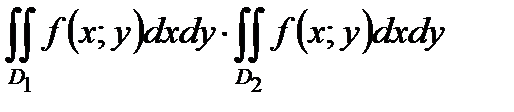
Б) 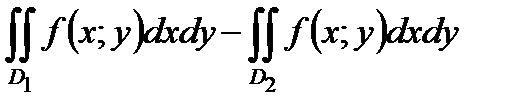
*В) 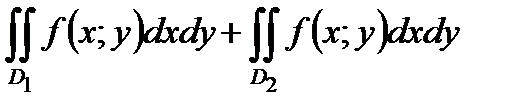
Г) 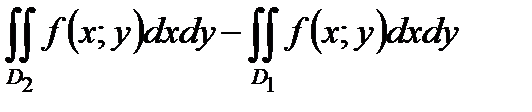
73. Пусть область 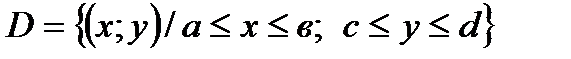 . Тогда двойной интеграл
. Тогда двойной интеграл 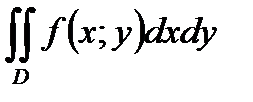 равен
равен
А) 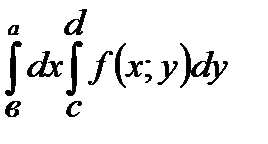
Б) 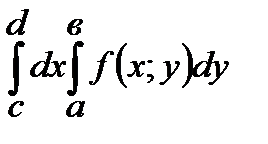
В) 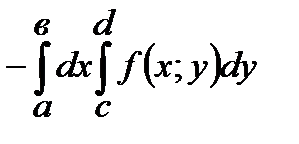
*Г) 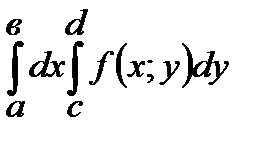
74. 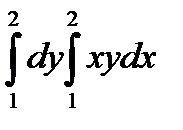 равен
равен
А) 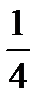
Б) 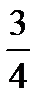
В) 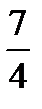
Г) 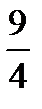
75. Пусть функция 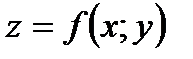 определена в области
определена в области 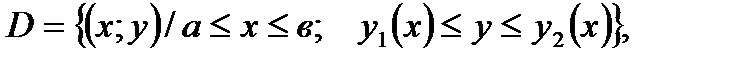 где
где 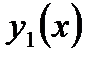 и
и 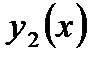 - непрерывные функции,
- непрерывные функции, 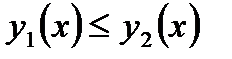 для
для 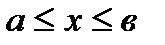 . Тогда
. Тогда 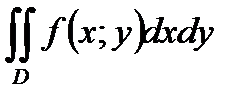 равен
равен
*А) 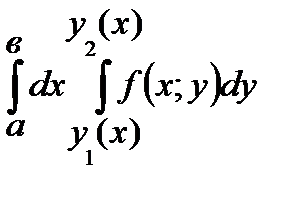
Б) 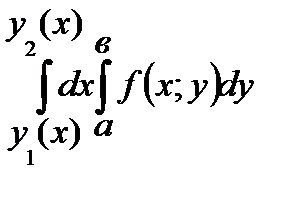
В) 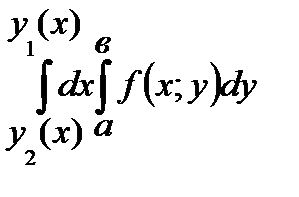
Г) 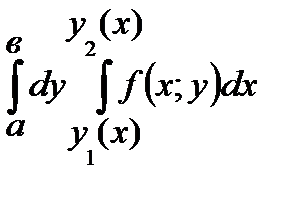
76. Пусть функция 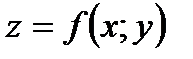 определена в области
определена в области 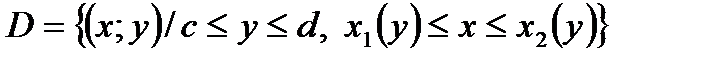 где
где 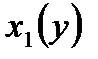 и
и 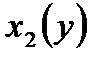 - непрерывные функции,
- непрерывные функции, 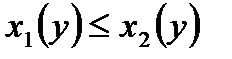 для
для 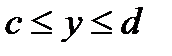 . Тогда
. Тогда 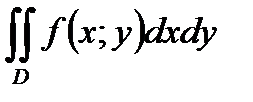 равен
равен
А) 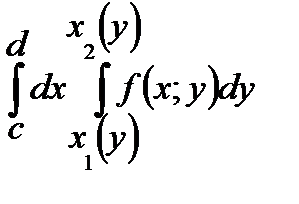
Б) 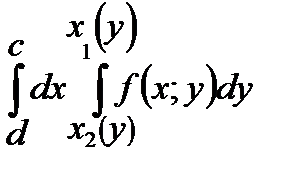
В) 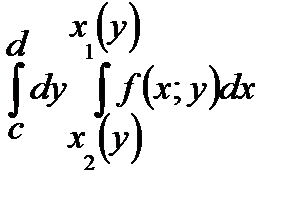
*Г) 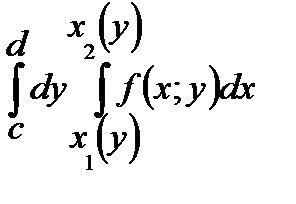
77. При переходе к полярным координатам 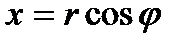
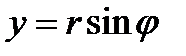 формула замены переменных в двойном интеграле принимает вид:
формула замены переменных в двойном интеграле принимает вид:
А) 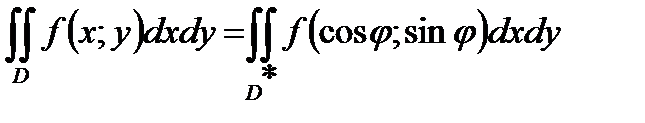

Б) 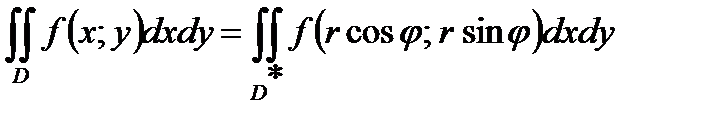
В) 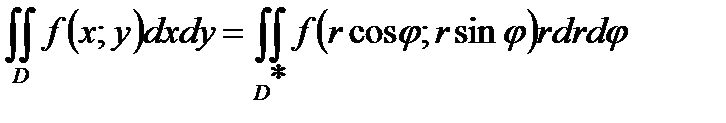
Г) 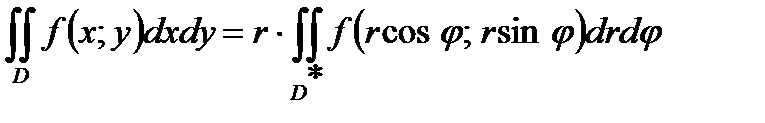
78. Объем V криволинейного цилиндра, ограниченного сверху поверхностью
z=f (x,y) > 0, снизу плоскостью z = 0 и с боковых сторон цилиндрической поверхностью, у которой образующие параллельны оси OZ, а направляющей служит контур области D, вычисляется по формуле.
А) V = 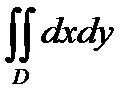
Б) V = 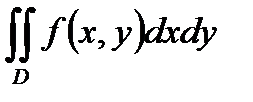
В) V = 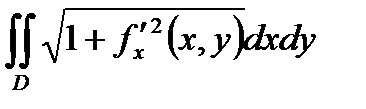
Г) V = 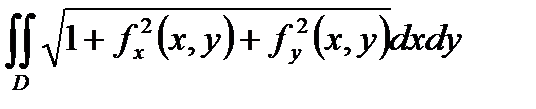
79. Площадь S области D может быть вычислена по формуле:
А) S = 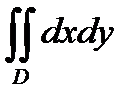
Б) S = 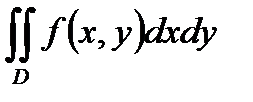
В) S = 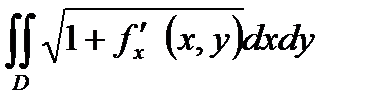
Г) S = 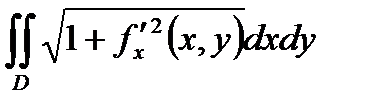
80. Пусть поверхность задана уравнением: z=f (x,y), а проекцией этой поверхности на плоскость XOY является областьD. Тогда площадь поверхности может быть вычислена по формуле:
А) S = 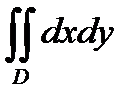
Б) S = 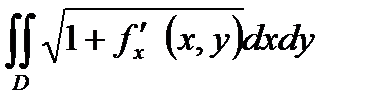
В) S = 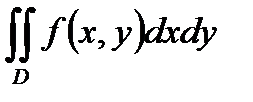
Г) S = 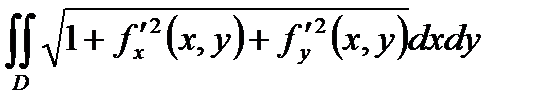
81. Массу m пластинки, занимающей в плоскости XOY некоторую область D с плотностью 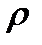 (x,y) можно вычислить по формуле:
(x,y) можно вычислить по формуле:
А) m = 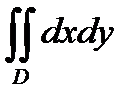
Б) m = 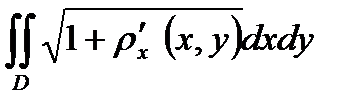
В) m = 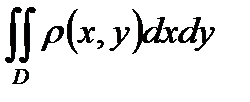
Г) m = 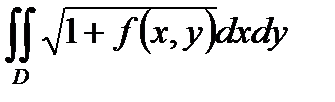
82. Статический момент относительно оси OY пластинки, занимающей в плоскости OXY некоторую область D и имеющей плотность 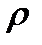 (x,y) вычисляется по формуле:
(x,y) вычисляется по формуле:
А) 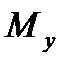 =
= 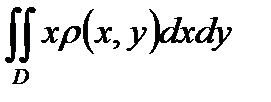
Б) 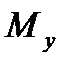 =
= 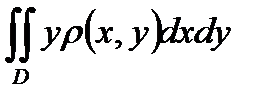
В) 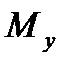 =
= 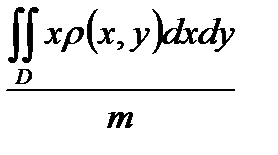
Г) 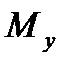 =
= 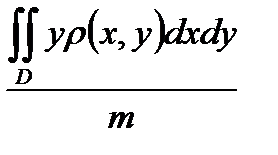
83. Статический момент относительно оси OX пластинки, занимающей в плоскости OXY некоторую область D и имеющей плотность 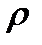 (x,y) вычисляется по формуле:
(x,y) вычисляется по формуле:
А) 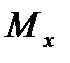 =
= 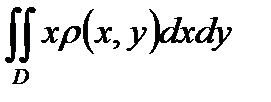
Б) 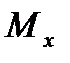 =
= 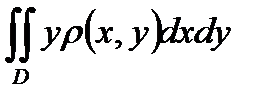
В) 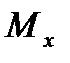 =
= 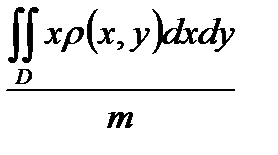
Г) 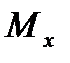 =
= 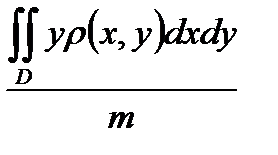
84. Координаты xc центра масс пластинки, имеющей плотность 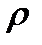 (x,y) и занимающей в плоскости OXY некоторую область D, определяется формулой.
(x,y) и занимающей в плоскости OXY некоторую область D, определяется формулой.
А)Xc = 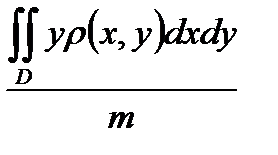
Б) Xc = 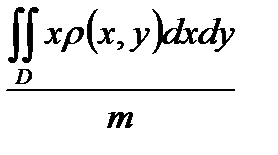
В) Xc = 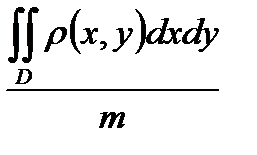
Г) Xc = 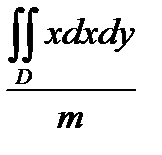
85. Координаты Yc центра масс пластинки, имеющей плотность 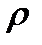 (x,y) и занимающей в плоскости OXY некоторую область D, определяется формулой.
(x,y) и занимающей в плоскости OXY некоторую область D, определяется формулой.
А)Yc = 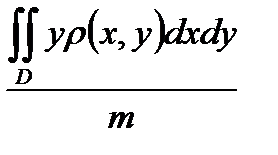
Б) Yc = 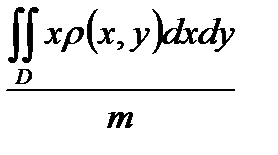
В) Yc = 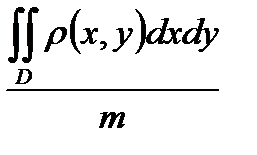
Г) Yc = 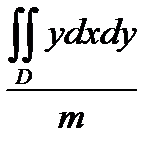
86. Координаты Xc центра масс однородной пластинки, занимающей в плоскости OXY некоторую область D, определяется формулой.
А)Xc = 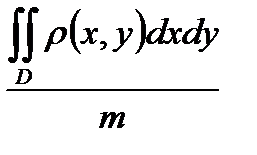
Б) Xc = 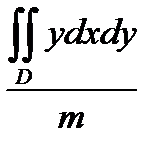
В) Xc = 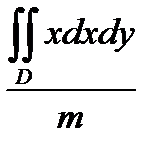
Г) Xc = 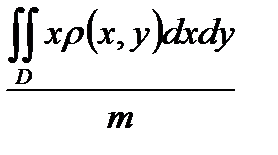
87. Координаты Yc центра масс однородной пластинки сть занимающей в плоскости OXY некоторую область D, определяется формулой.
А)Yc = 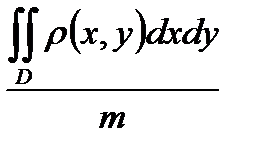
Б) Yc = 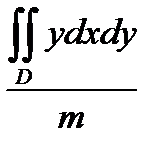
В) Yc = 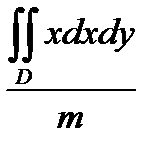
Г) Yc = 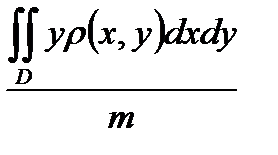
88.Дифференциальным уравнением называется
@А) уравнение, связывающее независимую переменную, неизвестную функцию и ее производные
Б) уравнение, содержащее производную независимой переменной
В) уравнение, которое легко интегрируется
Г) уравнение, которое решается дифференцированием
89.Решить дифференциальное уравнение - это означает
А) дифференцирование уравнения
@Б) интегрирование
В) нахождение независимой переменной
Г) нахождение производной функции
90.Дифференциальное уравнение называется линейным, если
А) неизвестная y в первой степени
Б) все производные неизвестной функции в первой степени
@В) неизвестная функция y и ее производные в первой степени
Г) решение записывается в виде явной функции
91.Обыкновенным дифференциальным уравнением называется уравнение
А) которое просто интегрируется
@Б) которое содержит только независимую переменную и неизвестную функцию
В) в котором неизвестная функция зависит от двух переменных
Г) в котором неизвестная функция зависит от одной переменной
92.Число постоянных в общем решении дифференциального уравнения определяется
@А) порядком дифференциального уравнения
Б) старшей степенью неизвестной функции
В) видом правой части
Г) старшей степенью независимой переменной
93.Общее решение дифференциального уравнения у" + а1у' + a2y = f(x) содержит
@А) две произвольные постоянные
Б) три произвольные постоянные
В) одну произвольную постоянную
Г) четыре произвольные постоянные
94.Частным решением дифференциального уравнения первого порядка называется
А) решение при y = x
@Б) решение, получающееся из общего решения при определенном значении постоянной C
В) решение при y = x2
Г) решение в виде частного двух функций
95.Дифференциальным уравнением первого порядка называется
А) уравнение, в котором независимая переменная x в первой степени
Б) уравнение, в котором неизвестная функция y в первой степени
@В) уравнение, которое содержит производную неизвестной функции только первого порядка
Г) уравнение первой степени
96.Дифференциальное уравнение называется линейным уравнением первого порядка, если
А) неизвестная функция y в первой степени
Б) независимая переменная x и неизвестная функция y в первой степени
В) сводится к уравнениям с разделяющимися переменными
@Г) неизвестная функция y и ее производная в первой степени
97.Функция f(x, y) является однородной функцией своих аргументов k- го порядка, если
@А) f(tx,ty) = tkf(x,y)
Б) y = xk
В) yk = x
Г) y = kx
98.Уравнение у' = f(x,y) называется однородным, если
А) f(x,y) = 0
@Б) функция f(x, y) является однородной функцией своих аргументов нулевого порядка
В) все переменные в первой степени
Г) неизвестная функция y в первой степени
99.Порядок дифференциального уравнения определяется
@А) порядком наивысшей производной, входящей в уравнение
Б) показателем степени независимой переменной
В) показателем степени неизвестной функции
Г) порядком расположения производной
100.Решением дифференциального уравнения у' = f(x,y) называется
А) любая непрерывная функция
@Б) функция y = ф(х), которая при подстановке в это уравнение обращает его в тождество
В) любая дифференцируемая функция
Г) любая интегрируемая функция
101.В линейном уравнении у' + p(x)y = q(x) функции p(x), q(x) являются
А) только возрастающими
Б) неизвестными функциями
@В) известными функциями независимой переменной x
Г) одна из функций известная, другая неизвестная
102.Вид частного решения линейного неоднородного дифференциального уравнения 2 - го порядка с постоянными коэффициентами зависит от
@А) вида правой части и корней характеристического уравнения
Б) порядка этого уравнения
В) общего решения однородного дифференциального уравнения 2 – го порядка
Г) произвольных постоянных
103.Если y1,y2 (y1 / y2 ≠const) – решения уравнения у" + а1у' + a2y = 0 и C1,С2 - некоторые постоянные, то общее решение этого уравнения имеет вид
А) y = С1у1+С2
@Б) y = С1у1+С2у2
В) y = (C1+C2)/(y1+y2)
Г) y=C1/y1 + C2 /y2
104.Характеристическое уравнение для линейного однородного уравнения
у" + а1у' + a2y = 0имеет вид
 2015-04-20
2015-04-20 3292
3292






