Правильные многогранники

Лабораторная работа №8(4 MT)

Цель:

• Построение правильных многогранников с помощью системы Mathematica;
• Развивать пространственное воображение за счет данного пакета.

Выпуклый многогранник называется правильным, если его гранями являются равные правильные многоугольники и в каждой вершине сходится одинаковое число граней.

Рассмотрим возможные правильные многогранники, гранями которых являются правильные треугольники:
Наиболее простым таким правильным многогранником является правильная пирамида (правильный тетраэдр) - рис.1, грани которой - правильные треугольники. Каждая его вершина является вершиной трех треугольников. Значит, сумма плоских углов при каждой вершине равна 180°.

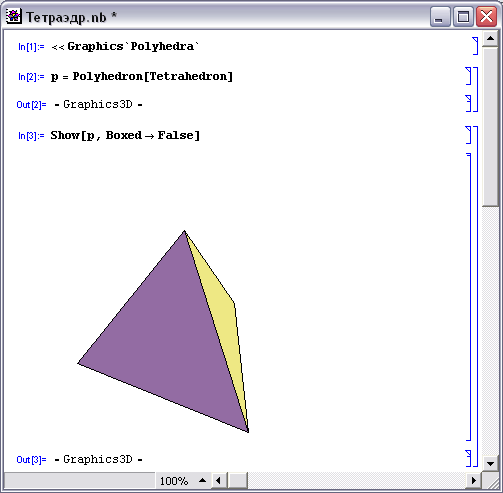
pис. 1. Тетраэдр

Многогранник, составленный из восьми правильных треугольников, называется октаэдром - рис.2. Каждая вершина октаэдра является вершиной четырёх треугольников. Значит, сумма плоских углов при каждой вершине равна 240°.

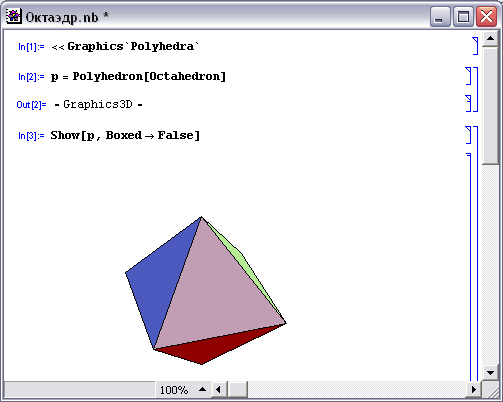
pис. 2. Октаэдр

Многогранник, составленный из двадцати правильных треугольников, называется икосаэдром - рис.3. Каждая вершина икосаэдра является вершиной пяти треугольников. Значит сумма плоских углов при каждой вершине равна 300°.

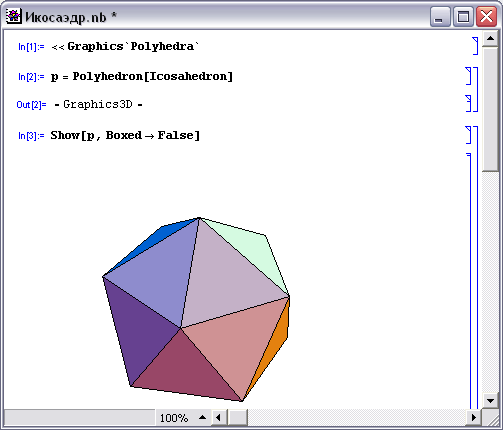
pис. 3. Икосаэдр

Заметим, что поскольку в вершинах выпуклого многогранника не может сходиться более пяти правильных треугольников, то других правильных многогранников, гранями которых являются правильные треугольники, не существует.

Аналогично поскольку в вершинах выпуклого многогранника может сходится только три квадрата, то кроме куба - рис.4, других правильных многогранников, у которых гранями являются квадраты, не существует.
Куб составлен из шести квадратов. Каждая вершина куба является вершиной трёх квадратов. Значит, сумма плоских углов при каждой вершине равна 270°.

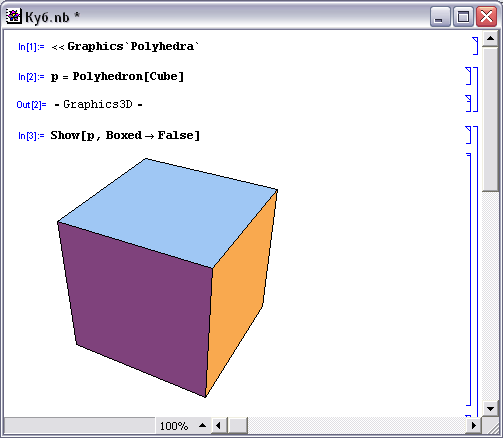
pис. 4. Куб

Многогранник, гранями которого являются правильные пятиугольники и в каждой вершине которого сходятся три грани, называется додекаэдром, так как его поверхность состоит из двенадцати правильных пятиугольников - рис.5. Значит, сумма плоских углов при каждой вершине равна 324°.

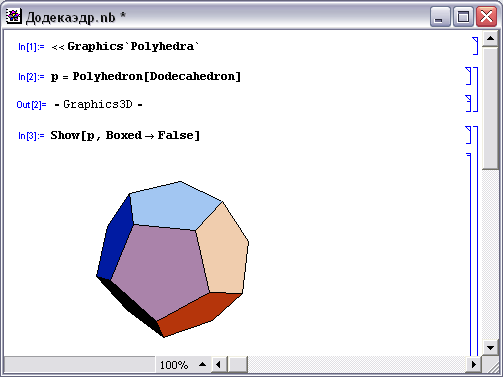
pис. 5. Додекаэдр

Можно доказать, что в вершинах выпуклого многогранника не могут сходиться правильные многоугольники с числом сторон больше пяти (теорема Эйлера), поэтому других правильных многогранников, кроме указанных, не существует, и, таким образом, имеется только пять правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.

Рассмотрим элементы симметрии правильных многогранников.
Правильный тетраэдр не имеет центра симметрии. Прямая, проходящая через середины двух противоположных рёбер, является его осью симметрии. Плоскость, проходящая через ребро тетраэдра перпендикулярно к противоположному ребру, является плоскостью симметрии. Правильный тетраэдр имеет три оси симметрии и шесть плоскостей симметрии. (Учитель изображает на доске все элементы симметрии для каждого многогранника).

Куб имеет один центр симметрии - точку пересечения его диагоналей. Прямые а и b, проходящие соответственно через центры противоположных граней и середины двух противоположных рёбер, не принадлежащие одной грани, являются его осями симметрии. Куб имеет девять осей симметрии. Плоскостью симметрии куба является плоскость, проходящая через любые две оси симметрии. Куб имеет девять плоскостей симметрии.

Правильный октаэдр, правильный икосаэдр и правильный додекаэдр имеют центр симметрии и несколько осей и плоскостей симметрии.