Лабораторная работа №8
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Цель работы
1. Вычислить заданный определённый интеграл 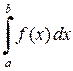 по формулам трапеций и Симпсона при
по формулам трапеций и Симпсона при 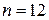 .
.
2. Оценить погрешность полученных результатов.
Содержание отчета
1. Постановка задачи.
2. Определение значений подынтегральной функции в точках деления.
3. Нахождение приближённого значения определённого интеграла по формуле трапеций и оценка погрешности.
4. Вычисление приближённого значения определённого интеграла по формуле Симпсона и оценка погрешности.
Все вычисления представить в виде таблицы аналогично приведенному ниже примеру.
Теоретические сведения
1. Формула трапеций. Пусть требуется вычислить приближённо 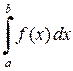 . Разбиваем отрезок
. Разбиваем отрезок 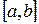 на
на 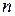 равных частей. Получаем точки деления:
равных частей. Получаем точки деления:
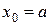 ,
, 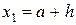 , …,
, …, 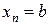 ,
,
где 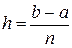 .
.
Обозначаем 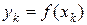
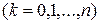 .
.
На каждом частичном отрезке 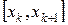
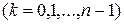 подынтегральную функцию
подынтегральную функцию 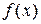 заменяем интерполяционным многочленом первой степени, построенным по двум узлам интерполяции (
заменяем интерполяционным многочленом первой степени, построенным по двум узлам интерполяции (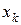 и
и 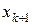 ), т.е. дугу графика подынтегральной функции
), т.е. дугу графика подынтегральной функции 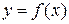 заменяем стягивающей её хордой. Отсюда получаем приближённое равенство
заменяем стягивающей её хордой. Отсюда получаем приближённое равенство
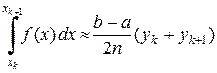 . (8.1)
. (8.1)
Сумма интегралов (8.1) по всем отрезкам дает общую квадратурную формулу трапеций
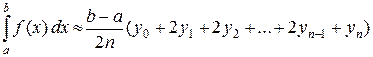 . (8.2)
. (8.2)
Погрешность этой формулы -
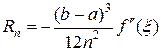 ,
,
где 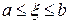 .
.
2. Формула Симпсона. Приближённое значение определённого интеграла 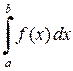 можно вычислить и другим спосо6ом. Разбиваем отрезок
можно вычислить и другим спосо6ом. Разбиваем отрезок 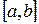 на
на 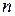 равных частей (
равных частей (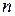 - чётное). Рассмотрим отрезки
- чётное). Рассмотрим отрезки 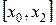 ,
, 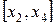 , …,
, …, 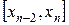 . На каждом сдвоенном отрезке
. На каждом сдвоенном отрезке 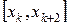 функцию
функцию 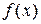 заменяем интерполяционным многочленом второй степени, построенным по трём узлам интерполяции (
заменяем интерполяционным многочленом второй степени, построенным по трём узлам интерполяции (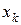 ,
, 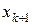 ,
, 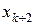 ), т.е. дугу графика подынтегральной функции
), т.е. дугу графика подынтегральной функции 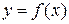 на каждом сдвоенном отрезке заменяем параболой, проходящей через точки
на каждом сдвоенном отрезке заменяем параболой, проходящей через точки 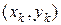 ,
, 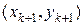 ,
, 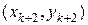 . Отсюда получаем приближённое равенство
. Отсюда получаем приближённое равенство
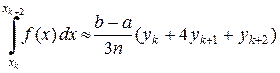 . (8.3)
. (8.3)
Сумма интегралов (8.3) по всем сдвоенным частичным отрезкам дает общую формулу Симпсона
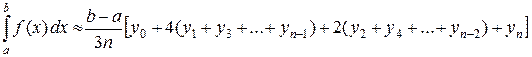 . (8.4)
. (8.4)
Погрешность этой формулы -
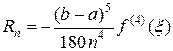 ,
,
где 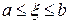 .
.
3. Оценка погрешности квадратурных формул. Обозначим: 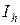 ,
, 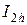 - приближённые значения определённого интеграла, вычисленные по квадратурной формуле с шагом
- приближённые значения определённого интеграла, вычисленные по квадратурной формуле с шагом 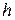 и
и 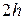 .
.
Отметим, что нахождение 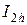 трудностей не вызывает, так как не требуется вычисления новых значений подынтегральной функции. Погрешность квадратурной формулы при вычислении интеграла с шагом
трудностей не вызывает, так как не требуется вычисления новых значений подынтегральной функции. Погрешность квадратурной формулы при вычислении интеграла с шагом 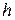 удовлетворяет неравенствам:
удовлетворяет неравенствам:
для формулы трапеций
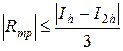 ; (8.5)
; (8.5)
для формулы Симпсона
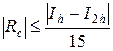 ; (8.6)
; (8.6)
Пример. Вычислить приближённо 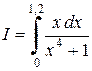 по формулам трапеций и Симпсона при
по формулам трапеций и Симпсона при 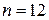 . Оценить погрешность полученных результатов.
. Оценить погрешность полученных результатов.
По условию 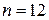 . Отсюда
. Отсюда 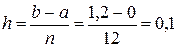 . Дальнейшие вычисления оформляем в виде таблицы.
. Дальнейшие вычисления оформляем в виде таблицы.
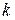
| 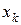
| 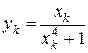
| Формула трапеций | Формула Симпсона | ||
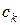
| 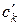
| 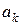
| 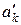
| |||
| 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 | 0.099990 0.199680 0.297589 0.390015 0.470588 0.531161 0.564470 0.567536 0.543445 0.500000 0.446410 0.390421 | |||||
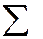
| 9,612189 | 4,767205 | 14,457172 | 7,228887 | ||
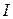
| 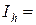 0,480609
0,480609
| 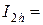 0,476720
0,476720
| 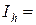 0,481905
0,481905
| 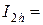 0,481925
0,481925
| ||
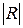
| 0,001297 <0,002 | 0,0000015 <0,000002 |
Ответ: 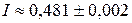 (по формуле трапеций);
(по формуле трапеций);
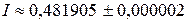 (по формуле Симпсона).
(по формуле Симпсона).
Рассмотрим порядок заполнения таблицы.
1. Определяем значения 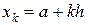 (
(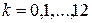 ). В данном случае
). В данном случае 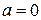 ,
, 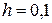
2. Находим значения подынтегральной функции в точках 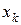 , т.е.
, т.е.
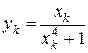 , (
, (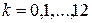 ).
).
3. Вычисляем приближённое значение определенного интеграла по формуле (8.2) c шагом 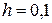 . При этом
. При этом 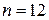 . Формула (8.2) имеет вид
. Формула (8.2) имеет вид
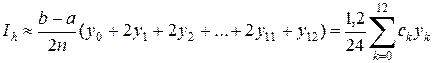 . (8.7)
. (8.7)
В столбце 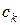 проставлены коэффициенты суммы (3,7), в строке
проставлены коэффициенты суммы (3,7), в строке 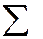 - значение
- значение 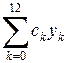 , в cтроке
, в cтроке 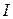 – ответ
– ответ 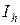 .
.
4. Для оценки погрешности вычисляем приближённое значение определенного интеграла по формуле (8.2) с шагом 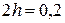 . При
. При 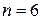 эта формула имеет вид
эта формула имеет вид
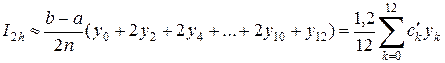 .
.
Так как точки 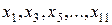 пропускаются, полагаем для них
пропускаются, полагаем для них 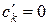 .
.
5. Оцениваем погрешность вычисления по формуле (8.2) с шагом 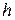 с помощью неравенства
с помощью неравенства
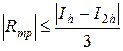 .
.
6. Находим приближённое значение определенного интеграла по (8.4) с шагом 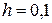 (при этом
(при этом 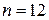 ):
):
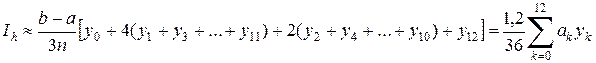 .
.
7. Вычисляем приближённое значение определенного интеграла по (3.4) с шагом 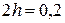 (при этом
(при этом 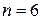 :
:
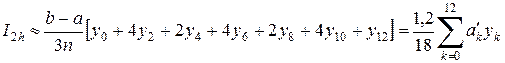 .
.
8. Оцениваем погрешность вычисления по (8.4) с шагом 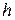 с учетом неравенства
с учетом неравенства
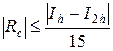 .
.
Варианты лабораторных работ
| Номер варианта | Определенный интеграл | Номер варианта | Определенный интеграл | |
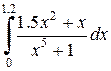
| 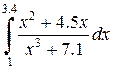
| |||
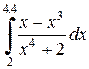
| 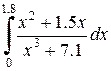
| |||
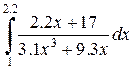
| 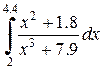
| |||
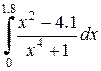
| 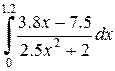
| |||
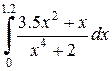
| 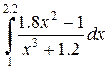
| |||
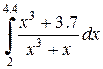
| 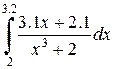
| |||
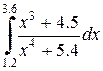
| 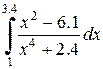
| |||

| 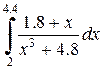
| |||
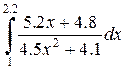
| 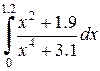
| |||
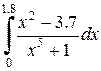
| 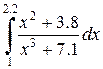
| |||
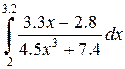
| 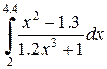
| |||
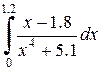
| 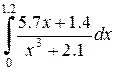
| |||
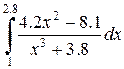
| 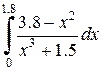
| |||
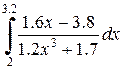
| 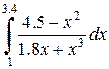
| |||
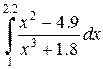
| 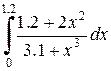
|
 2015-05-10
2015-05-10 230
230






