Методические указания. К лабораторным работам

к лабораторным работам

по дисциплине

«Системный анализ»

Донецк - 2014

Содержание

ВВЕДЕНИЕ 3

ЛАБОРАТОРНАЯ РАБОТА №1 Исследование решения прямой задачи 5

ЛАБОРАТОРНАЯ РАБОТА №2 Получение градиента критерия качества

идентификации 9

ЛАБОРАТОРНАЯ РАБОТА №3 Исследование решения сопряженной задачи 12

ЛАБОРАТОРНАЯ РАБОТА №4 Идентификация параметра неоднородного

линейного дифференциального уравнения 13

ЛИТЕРАТУРА 14

Введение

Рассмотрим краткие теоретические сведения, которые необходимы для дальнейшего изложения.

Определение 1. Пусть 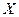- некоторое множество на числовой прямой. Говорят, что на этом множестве определена функция 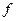, если каждому числу 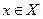поставлено в соответствие определенное число .

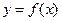Определение 2. Функция 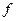называется функцией с интегрируемым квадратом на 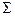, если интеграл

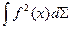
существует (конечен). Совокупность всех таких функций образует пространство функций с интегрируемым квадратом, которое обозначается через .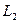

Определение 3. Отображения пространства 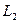во множество действительных чисел 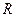называются функционалами, определенными на этом пространстве, или функционалами над этим пространством.

Определение 4. Пусть функци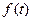и и 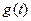определены на отрезке 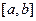. Скалярное произведение функци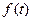й и 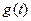определяется по формуле

.

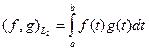Определение 5. Норма функции 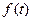определяется по формуле

.

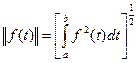Определение 6. Пусть заданы последовательность функций 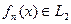, 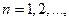и функция 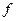, определенные на множестве 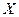. Указанная последовательность сходится к функции 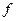равномерно на множестве 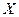, если для любого 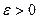существует такой номер 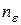, что если 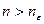, то для всех 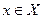выполняется неравенство .

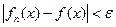Последовательность 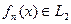называется равномерно сходящейся на множестве 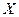, если существует функция, к которой она равномерно сходится на .

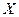Сущность равномерной сходимости последовательности функций состоит в том, что для любого 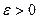можно выбрать такой номер 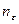, зависящий только от заданного 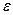и не зависящий от выбора точки 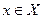, что при 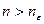неравенство 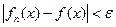будет выполняться всюду на множестве 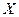, т.е. «графики» функций 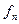расположены в « 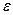-полоске», окружающей график функции .

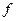Таким образом, в случае равномерной сходимости для любого 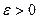при всех достаточно больших 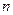(а именно при 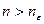) значения функции 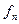приближают функцию 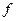с погрешностью, меньшей 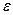, сразу на всем множестве .

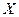Определение 7. Пусть 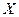и 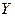- два нормированных пространства и 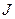- отображение, действующее из 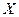в 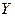и определенное на некотором открытом подмножестве 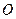пространства 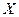. Назовем это отображение дифференцируемым в данной точке 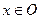, если существует такой линейный ограниченный оператор 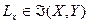, что для любого 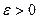можно найти 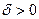, при котором из неравенства 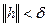следует неравенство

.

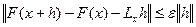То же самое сокращенно записывают так:

.

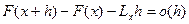Выражение 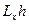(представляющее собой, очевидно, при каждом 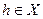элемент пространства 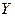) называется сильным дифференциалом (или дифференциалом Фреше) отображения 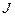в точке 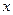. Сам линейный оператор 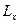называется производной, точнее, сильной производной отображения 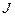в точке .

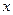Если отображение 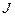дифференцируемо в точке 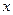, то соответствующая производная определяется единственным образом.

Определение 7. Множество метрического пространства называется компактом, если из любой последовательности его точек можно выделить подпоследовательность, сходящуюся к его точке.

Если 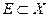, 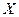- метрическое пространство, 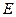- компакт, 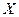- его точка прикосновения, то существует такая последовательность 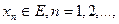что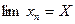

Всякое замкнутое подмножество компакта является компактом.

ЛАБОРАТОРНАЯ РАБОТА №1

Исследование решения прямой задачи

Цель работы: Приобретение навыков решения прямых задач.

Постановка задачи: Пусть некоторый процесс описывается дифференциальным уравнением второго порядка. Варианты заданий приведены в таблице. Необходимо получить и исследовать решение неоднородного уравнения с соответствующими граничными условиями. Экстремальная функция 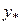необходима для выполнения третьей и четвертой лабораторных работ. Значение параметра 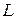получить у преподавателя.

№, п/п	Уравнение	Граничные условия	Экстремальная функция,
		,	,
		,	,
		,	,
		,	,
		,	,
	,	,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,
		,	,

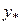
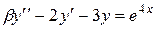
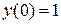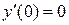
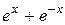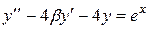
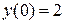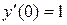
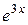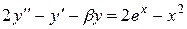
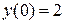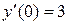
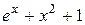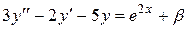
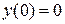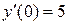
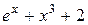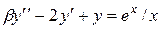
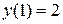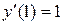
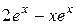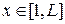
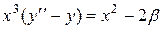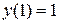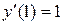
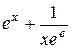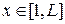
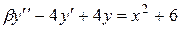
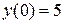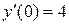
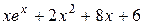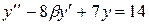
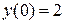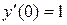
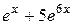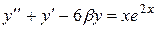
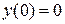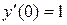
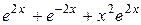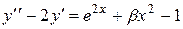
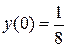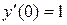
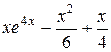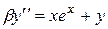
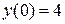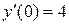
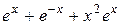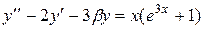
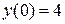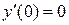
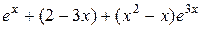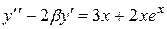
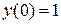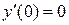
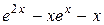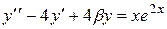
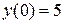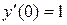
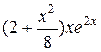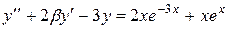
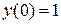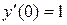
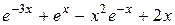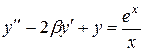
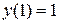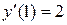
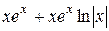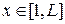
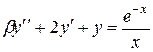
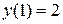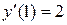
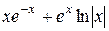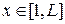
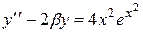
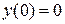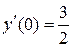
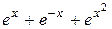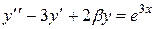
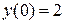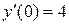
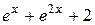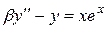
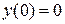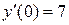
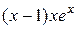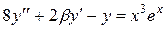
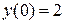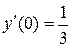
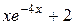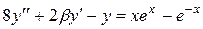
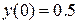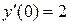
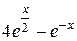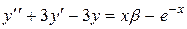
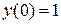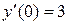
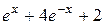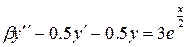
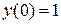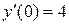
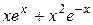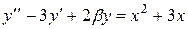
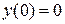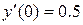
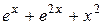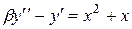
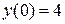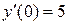
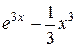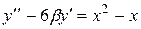
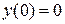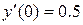
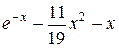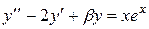
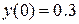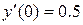
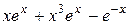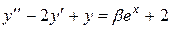
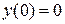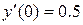
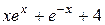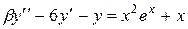
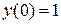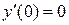
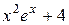Теоретическая часть

1⁰. Однородное уравнение. Линейное уравнение 2-го порядка с постоянными коэффициентам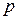и и 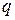без правой части имеет вид

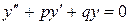(1.1)

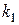Если и 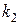- корни характеристического уравнения

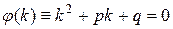, (1.2)

то общее решение уравнения (1.1) записывается в одном из следующих трех видов:

1) 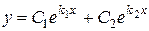, есл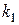и и 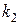вещественны и ;

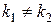2) 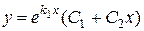, если ;

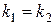3) 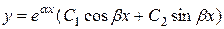, есл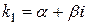и и ().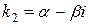

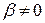2⁰. Неоднородное уравнение. Общее решение линейного неоднородного дифференциального уравнения

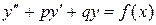(1.3)

можно записать в виде суммы

,

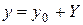где 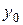- общее решение соответствующего уравнения (1.1) без правой части, определяемое по формулам 1.1) ­– 1.3), и 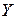- частное решение данного уравнения (1.3).

Функция 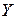может быть найдена методом неопределенных коэффициентов в следующих простейших случаях:

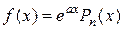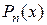1. , где - многочлен степени .

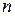Если 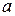не является корнем характеристического уравнения (1.2), т.е. 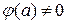, то полагают 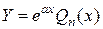, где 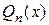- многочлен степени 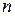с неопределенными коэффициентами.

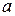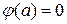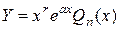Если есть корень характеристического уравнения (1.2), т.е. , то , где 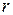- кратность корня 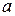( 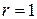или ).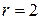

2. .

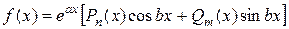Если 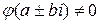, то полагают

,

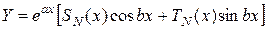где 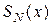и 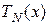- многочлены степени .

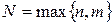Если же 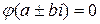, то

,

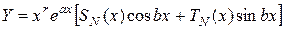где 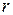- кратность корней 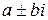(для уравнений 2-го порядка ).

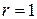В общем случае для решения уравнения (1.3) применяется метод вариации произвольных постоянных. Если известна фундаментальная система решений 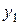, , 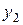…, 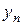однородного уравнения

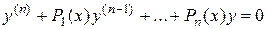, (1.4)

где 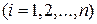- непрерывные коэффициенты, то общее решение соответствующего неоднородного уравнения

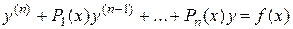, (1.5)

где 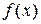- непрерывная функция, может быть найдено по формуле

,

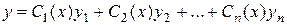то функции 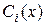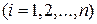определяются из системы уравнений

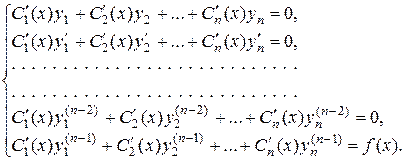
3⁰. Принцип наложения решений. Если правая часть уравнения () есть сумма нескольких функций

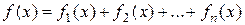
и 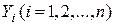- соответствующие решения уравнений

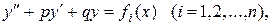
то сумма

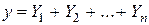
является решением уравнения (1.1).

Порядок выполнения работы

1. Получить аналитическое решение дифференциального уравнения с соответствующими граничными условиями.

2. Проанализировать влияние значения параметра 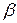на получаемое решения. С этой целью для разных трех значений 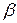построить графики зависимостей .

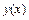Контрольные вопросы

1. Проанализировать метод решения линейного неоднородного дифференциального уравнения второго порядка.
2. Сущность метода вариации произвольных постоянных.
3. Анализ результатов решения работы.

ЛАБОРАТОРНАЯ РАБОТА №2

Получение градиента критерия качества идентификации

Цель работы: Приобретение навыков получения аналитического выражения градиента критерия качества в задаче идентификации.

Постановка задачи

Пусть функция 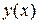удовлетворяет уравнению (1.3) с соответствующими краевыми условиями. Идентифицировать параметр 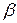, доставляющий минимум функционалу:

,

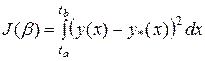где 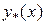- экспериментальное значение функции .

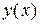Получить явное выражение для градиента 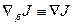, используя модифицированный метод множителей Лагранжа [3].

Теоретическая часть

Согласно [3], рассмотрим способ определения градиента (производной Фреше) критерия качества идентификации 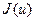для задачи идентификации параметра 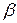. В нашем случае .

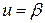В задачах идентификации аргумент 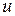присутствует в функционале 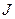всегда неявно. При этом 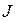зависит явно только от состояния системы, то есть от функции 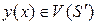, где 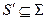, 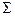- пространственная область функционирования системы, 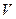- пространство состояний системы. Будем считать, что состояние системы корректно определяется через управление 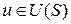. Пространственная область 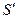определения целевого функционала и 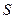определения управления, в общем случае, не совпадают друг с другом. Пусть пространство состояний 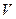и управлений 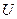- действительные гильбертовы с интегрируемым квадратом, т.е. 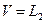и .

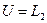Запишем уравнения системы в общей символической форме:

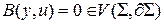, (2.1)

где 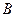обозначает дифференциальные операторы системы, определенные на пространственном множестве 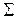вместе с операторами на соответствующих частях границы .

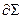Критерий качества идентификации запишем в виде:

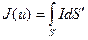, (2.2)

где 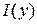- заданная функция аргумента .

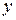Метод определения градиента 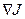является модернизацией классического метода множителей Лагранжа. Он включает в себя следующие этапы.

1. Линеаризация задачи управления в некоторой точке 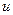. Данная процедура реализуется варьированием целевого функционала 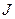и уравнений системы.

Вариации управления 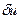, согласно (2.1), вызывают вариации состояния 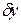. В результате варьирования (2.1) и (2.2) получаем:

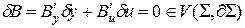, (2.3)

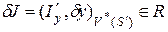. (2.4)

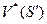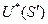Круглые скобки с индексами и представляют собой скалярные произведения в сопряженных пространствах 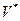и 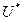на множестве .

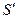Выражения (2.3) и (2.4) принадлежат разным пространствам. Уравнение (2.3) линеаризованной системы принадлежит функциональному пространству состояний 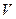, а линеаризованный функционал (2.4) – числовому пространству .

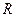2. Отображение линеаризованных уравнений системы при помощи соответствующих линейных функционалов 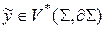(множители Лагранжа) из пространства 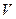в пространство 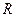. При этом, из уравнения (2.3) получаем:

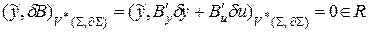. (2.5)

Поскольку здесь значение 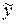может быть произвольным, то зависимость вариации 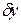от 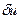в системе (2.5) исчезает и мы можем перейти к следующему этапу.

3. Преобразование отображений вариаций системы (2.5) к отображениям независимых вариаци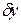й и 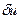(аналог тождества Лагранжа):

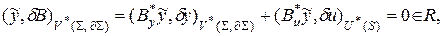(2.6)

где 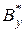, 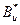- некоторые сопряженные операторы.

Теперь условия (2.4), (2.6) задачи управления (2.1), (2.2) записаны в одинаковых пространствах.

4. Объединение элементов задачи оптимизации в одинаковых пространствах. Поскольку линейным пространствам свойственна аддитивность их элементов, то можно записать:

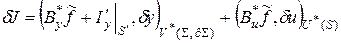. (2.7)

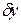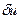5. Выделение градиента целевого функционала. Учитывая тот факт, что первая вариация – это главная линейная часть приращения функционала, получаем, что коэффициенты при аргументах и представляют собой компоненты градиента 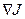, т.е.

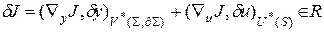. (2.8)

На данном этапе преобразований целесообразно устранить неоднозначную связь между вариациями управления 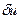и состояния 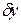. Это можно сделать, если задать значение линейного функционала 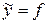из условия:

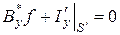. (2.9)

Данное условие называется сопряженной задачей.

Теперь первая вариация целевого функционала выражается только через вариацию управления:

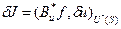, (2.10)

откуда следует, что градиент целевого функционала – это

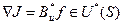. (2.11)

Значение 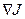определяется через решение 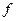линейной сопряженной задачи (2.9).

Примеры получения градиента критерия качества идентификации смотри в лекционной части дисциплины.

Порядок выполнения работы

1. Проварьировать целевой функционал 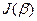и уравнение (1.3) совместно с начальными условиями по функции состояния 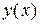и идентифицируемому параметру .

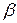2. Отобразить линеаризованное уравнение (1.3), с граничными условиями в пространство 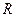при помощи множителей Лагранжа .

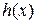3. Преобразовать отображения вариаций системы к отображениям независимых вариаци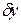й и .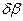

4. Объединить элементы задачи в одинаковых пространствах.

5. Выделить градиент .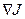

6. Получить сопряженную задачу.

7. Проанализировать идентифицируемость параметра .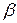

Контрольные вопросы

1. Запишите оператор Гамильтона.
2. Градиент функционала вектор или функция? Почему?
3. Проанализируйте этапы определения градиента целевого функционала.
4. В задаче идентификации покажите функцию состояния и идентифицируемый параметр.
5. Проанализируйте полученный градиент целевого функционала и соответствующую краевую задачу для множителя Лагранжа.

ЛАБОРАТОРНАЯ РАБОТА №3

Исследование решения сопряженной задачи

Цель работы: Приобретение навыков решения сопряженных задач.

Постановка задачи

В результате выполнения лабораторной работы №2 получена задача для множителя Лагранжа вида (2.9). Необходимо получить и исследовать аналитическое и численное решение полученной задачи.

Теория подробно расписана в теоретической части к лабораторной работе №1.

Порядок выполнения работы

1. Получить аналитическое и численное решение полученной задачи для множителя Лагранжа.

2.Проанализировать влияние целевого функционала на получаемое решение. С этой целью сопоставить аналитическое и численное решение прямой и сопряженной задачи. В чем отличие данных задач и их решений?

3. Построить графики зависимостей 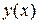для разных значений параметра .

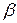Контрольные вопросы

1. Проанализировать влияние целевого функционала на получаемое решение сопряженной задачи.

2. Сопоставить и проанализировать начальные условия прямой и сопряженной задач.

3. Для чего необходимо получать решение сопряженной задачи?

ЛАБОРАТОРНАЯ РАБОТА №4

Идентификация параметра неоднородного линейного дифференциального уравнения

Цель работы: Приобретение навыков идентификации параметра неоднородного дифференциального уравнения второго порядка.

Постановка задачи

Идентифицировать параметр 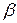дифференциального уравнения (1.3), доставляющий минимум целевому функционалу

,

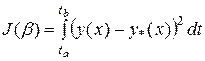где 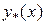- экспериментальное значение функции .

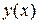Теоретическая часть

Рассмотрим основы прямого экстремального подхода [3], основанного на непосредственной минимизации целевого функционала 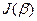различными экстремальными методами. Он очень нагляден и относительно просто реализуем. Идентифицируемый параметр 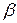определяется итерационно в процессе направленного спуска от начального приближения в сторону минимума целевого функционала.

Рассмотрим методы минимизации целевого функционала на основе его градиента.

Для минимизации целевых функционалов обычно используются градиентные методы [2, 3]:

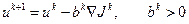, (4.1)

где 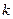- номер итерации, 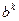- число, регулирующее глубину спуска в точке 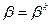в направлении градиента 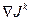. Число 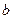и определяется на первой итерации из выражения [3]:

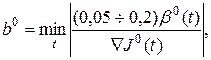(4.2)

где 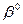- начальное приближение идентифицируемого параметра.

В зависимости от способа выбора числа 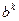можно получить различные варианты градиентного метода [2, 3]. Существуют различные способы выбора величины 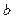в методе (4.1).

Если 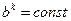на каждой итерации, то алгоритм (4.1) называется методом наискорейшего спуска [2, 3].

Часто в градиентных алгоритмах минимизации используют не метод наискорейшего спуска, а так называемый метод монотонного убывания [2, 3], в котором параметр 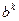принимается постоянным на всех итерациях и выполняется условие монотонности убывания целевого функционала .

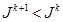В монографии [3] приблизительная реализация градиентного метода наискорейшего спуска осуществляется в виде алгоритма (4.1) с условием:

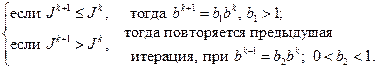(4.3)

Под словами “повторяется предыдущая итерация” подразумевается следующее. Пусть на 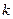-ой итерации целевой функционал увеличился, т.е. выполняется условие 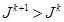. Тогда с этой итерации мы должны “вернуться назад” к приближению 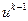и c этого приближения с новым числом 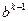, осуществлять следующее приближение по алгоритму (1.1) до тех пор, пока не выполнится условие 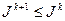. Глубина спуска на каждой итерации вдоль выбранного направления минимизации определяется числом .

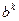Для увеличения скорости сходимости может быть использован близкий к методам второго порядка метод сопряженных градиентов [2, 3]:

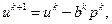(4.4)

где функция

,

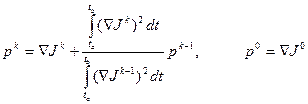а число 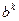выбирается постоянным на всех итерациях, или согласно (4.2). Необходимо помнить, что алгоритм (4.4) требует периодического “очищения” направления спуска от накапливающихся погрешностей, т.е. в процессе минимизации необходимо задавать направление спуска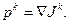

Для решения задачи идентификации предлагается применение прямого итерационного экстремального подхода с регулируемым направлением спуска [3]:

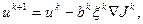(4.5)

где число 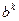определяет глубину спуска в направлении 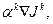и определяется формулой (4.3). Функция 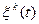регулирует направление спуска, может осуществлять быструю равномерную сходимость к оптимальному потоку тепла и определяется на первой итерации из выражения [4]:

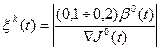. (4.6)

Если 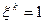, то алгоритм (4.5) превращается в градиентный метод (4.1). Как показано в монографии [3], алгоритм (4.5) является регуляризирующим, т.е. обеспечивает принадлежность каждого нового приближения 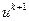компакту корректности. Степень регуляризации на каждой итерации определятся параметрами шага 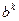и 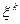. Чем меньше значение и, тем сильнее регуляризируется решение и замедляется сходимость алгоритма. Функция 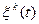позволяет регулировать направление спуска. Поэтому алгоритм (4.5) называется методом минимизации с регулируемым направлением спуска.

Порядок выполнения работы

1. Задать экстремальное значение идентифицируемого параметра .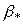

2. Решить прямую задачу в соответствии со своим вариантом и получить зависимость .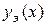

3. Реализовать алгоритм (1) программным методом.

4. Задать начальное приближение .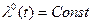

5. Рассчитать параметр шага ;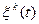

6. Выбрать соответствующий алгоритм минимизации целевого функционала 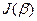в соответствии с требованием равномерной сходимости функции 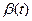к искомому значению.

7. На каждой итерации выводить значения целевого функционала, градиента, нормы градиента функционала, и нормы разности .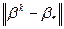

8. Проанализировать полученный результат.

Контрольные вопросы

1. Проанализировать метод наискорейшего спуска.
2. Проанализировать метод сопряженных градиентов.
3. Проанализировать метод с регулируемым спуском.
4. Какое значение должна принимать норма градиента в точке минимума целевого функционала?

Литература

1. Бугров Я. С., Никольский С.М. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного: Учебник для ВУЗов.- 3-е изд. – М.: Наука, 1989. -464 с.

2. Васильев Ф.П. Численные методы решения экстремальных задач. М.:Наука.1988.-552 с.

3. Толстых В.К. Прямой экстремальный подход для оптимизации систем с распределенными параметрами. - Донецк: Изд. “Юго-Восток", 1997.-177 с.