|
Если рассматривать в сильный микроскоп жидкость, в которой находятся маленькие, не растворяющиеся в жидкости частицы (например, частицы краски в воде), то в поле зрения микроскопа можно увидеть массу хаотически движущихся частиц. Это явление называется броуновским движением.
Броуновское движение - результат соударения молекул жидкости со взвешенными в ней частицами. Так как молекулярное движение хаотично, то частица получает больший импульс то с одной стороны, то с другой стороны и в результате также приходит в хаотическое движение.
Количественная теория броуновского движения была впервые разработана Эйнштейном и, независимо от него, Смолуховским. Основное соотношение этой теории, вывод которого приведен в рекомендуемой литературе, называется законом Эйнштейна. Этот закон гласит: среднее значение квадрата проекции перемещения броуновской частицы за данный промежуток времени вдоль определенного направления пропорционально этому промежутку времени т.е.  , (1) , (1)
где коэффициент пропорциональности
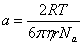 . (2) . (2)
Подставляя (2) в (1), получим:
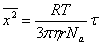 , (3) , (3)
где 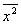 - средний квадрат проекции перемещения броуновской частицы вдоль определенного направления; - средний квадрат проекции перемещения броуновской частицы вдоль определенного направления;
 - промежуток времени перемещения частицы; - промежуток времени перемещения частицы;
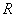 - универсальная газовая постоянная; - универсальная газовая постоянная;
 - абсолютная температура эмульсии; - абсолютная температура эмульсии;
 - коэффициент вязкости среды, в которой движутся броуновские частицы; - коэффициент вязкости среды, в которой движутся броуновские частицы;
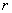 - радиус броуновской частицы; - радиус броуновской частицы;
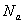 - число Авогадро. - число Авогадро.
Формула (3) позволяет вычислить среднее значение квадрата перемещений, причем среднее берется по всем частицам, участвующим в движении. Но эта формула справедлива и для среднего значения квадрата 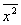 многих последовательных перемещений одной единственной частицы за равные промежутки времени. многих последовательных перемещений одной единственной частицы за равные промежутки времени.
С экспериментальной точки зрения удобнее наблюдать именно перемещение одной частицы. Такие наблюдения и были проведены французским физиком Перреном.
Предлагаемый в данной работе способ определения размеров частиц основан на использовании закона Эйнштейна (см. формулу 3).
Описание установки и методика измерений
- Описание установки. Установка состоит из микроскопа, рисовального аппарата, осветителя и наклонного столика. Устройство микроскопа и рисовального аппарата и правила использования их в работе следует предварительно изучить по заводским описаниям этих приборов, а также по книге "Физический практикум" под ред. проф. В.И. Ивероновой, 1963 г., стр. I79-I8I.
- Приготовление эмульсии. В качестве броуновских частиц можно взять частицы краски, растворенной в воде, или частицы эмульсии канифоли в растворе спирта и воды. В последнем случае эмульсия приготавливается заранее следующим образом:
10 см 2%-гo раствора канифоли в спирте вливают по
каплям в 15 дистиллированной воды при дистиллированной воды при
тщательном перемешивании. Получившаяся молочно-
белая эмульсия ставится не менее чем на сутки для
отстаивания. За это время наиболее крупные частицы
выпадают в осадок. Слой эмульсии над осадком
берется для опыта.
Примечание. Перед началом опытов полезно растворить в полученной эмульсии красную краску кармин и раствор центрифугировать.
- Определение увеличения установки (микроскопа с рисовальным аппаратом).
а) Отрегулировав с помощью осветителя и зеркала освещенность поля зрения микроскопа, укрепляют на его тубусе рисовальный аппарат.
б) Перед объективом микроскопа помещают объект-микрометр. На специальном столике укрепляют лист бумаги (миллиметровой) и добиваются того, чтобы через рисовальный аппарат хорошо были видны на фоне бумаги штрихи объект-микрометра и остриё карандаша. Наносят эти штрихи на миллиметровую бумагу. Зная цену деления объект-микрометра, определяют увеличение установки (микроскопа с рисовальным аппаратом).
- Проверка закона Эйнштейна.
- В углубление на предметном стекле, предварительно протертом спиртом, вносят 2-3 капли эмульсии и препарат накрывают чистым покровным стеклом так, чтобы под покровным стеклом не было пузырьков воздуха. Избыток эмульсии под покровным стеклом удаляют при помощи фильтровальной бумаги.
- Препарат помещают перед объективом и производят фокусировку микроскопа, добиваясь отчетливой видимости броуновских частиц и острия карандаша на фоне листа миллиметровой бумаги, помещенного под зеркалом рисовального аппарата.
- Выбрав отчетливо видимую движущуюся броуновскую частицу, совмещают с её изображением кончик карандаша и отрезками прямой соединяют положения броуновской частицы через одинаковые промежутки времени, например, через 5,10,15,20 секунд. В результате на листе миллиметровой бумаги получают проекцию траектории перемещения броуновской частицы. Точки нумеруют (см. рис.).

Затем проектируют полученную траекторию броуновской частицы на выбранную определенным образом прямую ОХ и получают точки 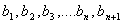 . Обозначив отрезки проекций . Обозначив отрезки проекций  , вычисляют квадраты проекций перемещения броуновской частицы, например, через время , вычисляют квадраты проекций перемещения броуновской частицы, например, через время 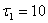 секунд. секунд.
- Затем вычисляют средний квадрат проекции перемещения броуновской частицы через 10 секунд:
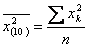 , к=1,2,3,..n. , к=1,2,3,..n.- Пользуясь тем же рисунком траектории броуновской частицы (см. рис.), вычисляют средние квадраты проекций перемещения броуновской частицы через промежутки времени
 c, c, c. c.
 ; ;
 . .
е) Если  , то закон Эйнштейна применим. , то закон Эйнштейна применим.
- Определение радиуса броуновской частицы. Из формулы (3) выражают радиус броуновской частицы
 (4) (4)
и вычисляют его, взяв из таблиц  и и
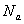 =6,023 x I023 =6,023 x I023 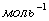 . .
Примечание. Если 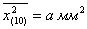 увеличение установки С, то в системе СГС получим увеличение установки С, то в системе СГС получим
 . .
|


 ;
; .
. , то закон Эйнштейна применим.
, то закон Эйнштейна применим.








