Обратная матрица. Свойства
Определим операцию деления матриц как операцию, обратную умножению. Определение. Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию: Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну. Пример. Дана матрица А =
Таким образом, А-1= Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу: где Мji- дополнительный минор элемента аji матрицы А. Пример. Дана матрица А = M11= 4; M12= 3; M21= 2; M22= 1 Таким образом, А-1= Cвойства обратных матриц.Укажем следующие свойства обратных матриц: 1) (A-1)-1 = A; 2) (AB)-1 = B-1A-1
Отметим, что матрицы
Пример. Вычислить определитель
|
|
Элементарные преобразования системы линейных уравнений Вернуться в оглавление: Высшая математика |

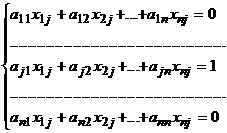 ,
,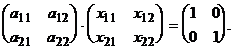
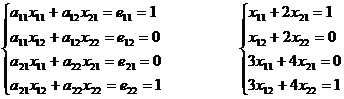
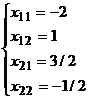
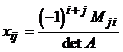 ,
,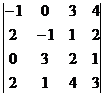 .
.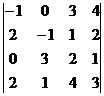 = -1
= -1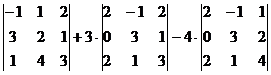
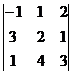 = -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10.
= -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10. =
= 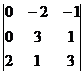 = 2(0 – 2) – 1(0 – 6) = 2.
= 2(0 – 2) – 1(0 – 6) = 2.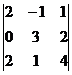 =
= 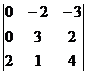 = 2(-4) – 3(-6) = -8 + 18 = 10.
= 2(-4) – 3(-6) = -8 + 18 = 10.








