Нелинейные колебательные процессы в мультистабильных системах

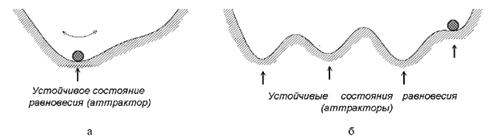
Наряду с динамическими переменными, зависимость которых от времени составляет сущность колебательного процесса, при рассмотрении колебательных систем приходится иметь дело также с параметрами, постоянными во времени, но, от задания которых, может зависеть характер реализующегося в системе режима.

Например, качественные изменения колебательных режимов, возникающие при медленном изменении параметров системы, могут приводить к появлению, так называемых бифуркаций. Одной из распространенных проявлений бифуркаций и является возбуждение автоколебаний в нелинейных системах при переходе параметра через критическое, бифуркационное значение амплитуды, например, при плавном увеличении коэффициента усиления колебаний.

Чтобы познакомиться с дальнейшими примерами бифуркаций, обратимся к одной из самых простых колебательных систем, представленной шариком в лунке рис. 14.3.

Рис. 14.3 Шарик в лунке в случае одного (а) и нескольких (б) устойчивых положений равновесия.

В присутствии трения шарик будет совершать колебания вблизи точки минимума, приходя, в конце концов, в состояние устойчивого равновесия. Можно рассмотреть и более сложный случай и предположить, что профиль лунки имеет более одного минимума, то есть содержит несколько лунок, соответственно увеличится и число устойчивых состояний такой колебательной системы. В зависимости от того, какой была исходная координата и скорость шарика, он попадет в итоге в одну из лунок. В данном случае мы будем иметь дело с колебательной системой, имеющей несколько аттракторов, в качестве которых в данном случае выступают состояния устойчивого равновесия.

Если какая-нибудь колебательная система характеризуется наличием нескольких потенциально возможных установившихся состояний или колебательных режимов, то говорят, что имеет место мультистабильность.

В линейной системе мультистабильность невозможна. В частности, в данном примере с шариком наличие у профиля нескольких ямок с очевидностью требует, чтобы зависимость возвращающей силы от координаты частицы была нелинейной.

Предположим теперь, что форму профиля можно регулировать, изменяя параметры системы, так, что в процессе этой деформации могут появляться или пропадать локальные минимумы.

Одно из интересных явлений будет наблюдаться в ситуации, когда ямка, в которой располагается шарик, сближается с локальным максимумом и исчезает. Это бифуркация слияния устойчивого и неустойчивого состояний равновесия. После бифуркации локальный максимум исчезает, и система должна скачком перейти в новое состояние, достаточно удаленное от исходного. Говоря о скачке, мы имеем в виду, что координата частицы претерпит существенное изменение в итоге процесса перехода в новое состояние. Что касается развития этого процесса во времени, то на начальной стадии он будет достаточно медленным, так как локально профиль в области нахождения частицы практически плоский.

Рис. 14.4 Скачкообразное изменение состояния равновесия системы «шарик в лунке» при медленном изменении ее профиля.

Рис. иллюстрируют как изменяется состояние системы «шарик в лунке» при медленном изменении формы потенциального рельефа. При таком скачкообразном изменении состояния системы говорят о жесткой бифуркации или катастрофе.

Рис. 14.5 Изменение потенциального рельефа, соответствующее двум траекториям движения по плоскости параметров, приводящим к реализации двух различных состояний устойчивого равновесия.

В зависимости от того, как выбран путь на плоскости параметров при их медленном изменении, можно прийти в одну и ту же точку области бистабильности, имея результатом разные состояния равновесия.

Электромеханическая память.

Применение сканирующего СКВИД-микроскопа

Применения сверхпроводников в измерительной технике

Растровый (сканирующий) электронный микроскоп

Метод Брэгга

Вернуться в оглавление: Современные фундаментальные и прикладные исследования в приборостроении