Сигнал и его математическая модель

Сигнал электросвязи. В большинстве случаев сигнал элек­тросвязи можно рассматривать как меняющуюся во времени элек-трическую величину (напряжение, ток, электромагнитное колеба­ние, напряженность поля). Эти величины можно наблюдать и ре-гистрировать с помощью различных приборов, например осцилографа. После наблюдения сигнал будет задан в виде графика или таблицы как функция времени. Это представление назы-вают временной диаграммой. Один из примеров временной диаг-раммы дан на рис. 2.1, где изображена осциллограмма тока, про-текающего через микрофон. Такое представление является наглядным. На интервале (0, t₁) звуковые колебания на микрофон не воздействовали; на интервале (t₁, t₂) — воздействовало звуковое колебание определенного тона; на интервале (t₂, t₃) — сложные звуковые колебания.

Рис. 2.1. Временная диаграмма то­ка через микрофон

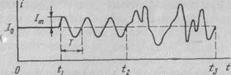
Однако временные диаграммы сигнала являются неудобными как для теоретических расчетов, так и для представления дли­тельных сигналов. Подсчитайте, какую длину будет иметь времен­ная диаграмма телеграфного сигнала при времени наблюдения 30 мин, если каждый кодовый символ длительностью 20 мс изо­бразить в масштабе 5 мм на символ. 450 метров! Поэтому для проведения всевозможных расчетов с сигналами возникает зада­ча их математического описания. Оно заключается в получении такого относительно простого математического выражения (фор­мулы, уравнения, неравенства и т. д.), по которому можно было бы вычислить необходимые свойства и параметры сигналов (мгно­венные значения, числовые характеристики и т. п.). Математиче­ское описание сигнала и называют его математической моделью.

Математическая модель отображает существенные свойства реального сигнала. Один и тот же реальный сигнал может быть представлен несколькими моделями. Например, отрезок гармо­нического колебания можно записать в виде u(t)=U_mcos(w₀t+p/2) или u(t)=U_msinw₀t.

Выбор наиболее подходящего для каждого конкретного сигнала математического выражения осу­ществляется, как правило, на основе анализа временной диаг­раммы. Это и есть выбор математической модели. Одна и та же математическая модель служит для описания тока, напряжения, напряженности поля и т. д. В дальнейшем математические моде­ли сигналов будут обозначаться символами латинского алфавита s(t), u(t), a(t), b(t). При этом не будет специально подчерки­ваться, что это не сам реальный сигнал, а его модель. Ведь эти представления адекватны. Обозначенные на обобщенной струк­турной схеме системы связи (см. рис. 1.1) сигналы в различных точках как раз и являются математическими моделями этих сиг­налов. Можно сказать: в реальных каналах действуют сигналы, а для расчетов используются их математические модели.

Пример 2.1. Составьте математическую модель сигнала, изображенного на -рис. 2.1, на интервале (0, t₁).

Из анализа временной диаграммы следует, что сигнал можно записать •в виде системы равенств

Примечание. Подобрать математическую формулу для отрезка (t₂, t₃) труд-чно из-за сложной формы сигнала.

Классы сигналов и их математическое пред­ставление. Разделение сигналов на классы можно провести по следующим признакам:

форме — простые и сложные;

информативности — детерминированные и случайные;

характеристикам —непрерывные, дискретные и цифровые.

Математической моделью простого сигнала является простая функция времени. Из простых сигналов в электросвязи находят применение гармонические сигналы, конечные и бесконечные по­следовательности импульсов, испытательные сигналы и др.

Гармонический сигнал, который часто называют гармоничес­ким колебанием, записывается в виде

u(t)=U_mcos(2pft+y₀) при -¥<t<¥, (2..1)

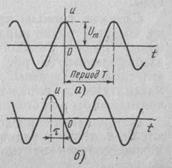
где U_m — максимальное значение (амплитуда); f — циклическая частота; y₀—начальная фаза. Параметры гармонического коле­бания U_m, f, y₀хорошо видны на рис. 2.2,а,б. Сдвиг по фазе (рис. 2.2,6) приводит к сдвигу гармонического колебания на время т влево. Начальная фаза y₀=2pt/T, циклическая частота f=l/T.

Достаточно часто при расчетах используется угловая частота w=2pf. Отметим, что гармоническое колебание (2.1) является мате­матической абстракцией. Реальный сигнал не может быть беско­нечным. Но если время существования сигнала t_и>>1, то такая математическая модель, например выходного напряжения гене­ратора, является приемлемой для расчетов. Ведь если с момен­та включения генератора до момента наблюдения прошло нес­колько миллионов периодов колебания, то все переходные про­цессы давно окончились. Можно считать, что генератор выдает гармоническое колебание.

Импульсными сигналами являются сигналы, отличные от ну­ля в течение ограниченного времени. Эти сигналы существуют лишь в пределах конечного отрезка (t_1,t₂) При этом различают видеоимпульсы (рис. 2.3,а) я радиоимпульсы (рис. 2.3,6). Если u_B(t) —видеоимпульс, то соответствующий ему радиоимпульс u_p(t)=u_в(t)cos(wt+y₀) (частота w и начальная фаза y₀ могут быть произвольными).

В радиоимпульсе u_B(t) называется огиба­ющей, а функция cos(wt+y₀) — заполнением. Параметрами видеоимпульса принято считать его амплитуду U_m, дли- тельность t_и, длительность фронта t_ф, длительность спада t_e. Происхождение термина «видеоимпульс» связано с тем, что впервые такие имлульсы начали применять для описания сигналов в телевидение

Рис. 2.2. Гармоническое колебание: а —начальная фаза y₀=0;

б- начальная фазаy₀>0

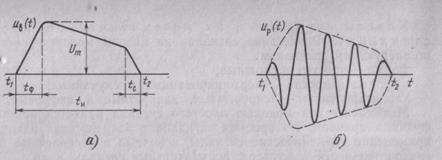
Рис. 2.3. Импульсные сигналы:

а — видеоимпульс; б — радиоимпулье

В электросвязи наибольшее применение находят одиночные импульсы или их периодическая последовательность, форма ко­торых приближается к прямоугольной. Для периодической после­довательности импульсов, кроме перечисленных выше параметров, вводится понятие скважности, определяемой как отношение пе­риода к длительности импульса: S=T/t_и

Бесконечно короткий видеоимпульс бесконечной амплитуды называется б-функцией (читается «дельта-функция»), которая за-

писывается в виде

d(t-t₀)=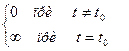

где to — момент действия импульса. Эта функция обладает ин­тересным свойством:

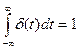
физически означающим, что хотя значение б-функции в точке /о и равно бесконечности, но площадь ее конечна и единична.

Широко используется б-функция при анализе различных ра­диотехнических цепей. Она является математической моделью прямоугольного импульса малой длительности и большой ампли­туды.

Сложные сигналы представляют собой такие функции време­ни, которые трудно выразить в виде простой математической фор­мулы. Пример сложного сигнала — отрезок речевого сигнала, изображенного на рис. 2.1. Большинство реальных сигналов — это сложные сигналы. Как же для них подобрать приемлемое математическое выражение? Причем желательно такое, которое подходило бы для большинства сигналов.

Математиками найдено такое решение. Им широко пользу­ются в электро- и радиотехнике. Подобно тому, как любое здание можно собрать из упорядоченного ряда простых конструкций, так и сигнал можно представить в виде ряда некоторых элемен­тарных (простых) функций y_k(t) называемых базисными:

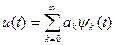, (2.2)

где a_k—коэффициенты разложения, зависящие от сигнала u(t)

Пример 2.2. Представить сигнал u₁(t), изображенный на рис. 2А,а,б в виде

ряда (суммы) элементарных функций.

Для наглядности разложения приведем графически на временной диаграм­ме. В качестве элементарных функций выберем последовательности прямоуголь­ных (рис. 2.4,в — вариант 1) или треугольных (рис. 2.4,г —вариант 2) импуль­сов единичной амплитуды. Длительность импульсов меньше длительности сиг­нала u₁(t) Графические построения показаны на рис. 2А,а,б. Коэффициенты a_kв данном примере равны значениям сигналав моменты времени.

Из сравнения рис. 2.4,а и б следует, что u₁(t) при одинаковом числе членов ряда в двух вариантах сумма треугольных функций более точно описывает заданный сигнал. Для увеличения точности необходимо увеличить число сла­гаемых ряда, что требует уменьшения их длительности.

Выбор системы базисных функций y_k(t) зависит от вида сиг-

нала и решаемой задачи. Но имеется общее правило — функции y_k(t) сами должны быть простыми, обеспечивать простое вычис­ление коэффициентов a_h и давать хорошую сходимость ряда,(2.2) к сигналу u(t) Выбор функциигчитается y_k(t) тем лучше, чем

меньше требуется составляющих ряда nдля представления сиг­нала u(t) с заданной точностью:

Рис.2.4. К представлению сигнала u(t) рядами простых функций:

при прямоугольных функциях; б —ряд при треугольных функциях;

в — прямобазисные функции; г — треугольные базисные функции

Детерминированные и случайные сигналы. Де­терминированным является сигнал, задаваемый функцией време­ни, по которой можно вычислить его мгновенные значения в лю-6ые моменты. Примерами таких сигналов являются приведенные ранее гармоническое колебание (2.1), видеоимпульсы с извест­ными параметрами. Детерминированные сигналы используются в технике связи как контрольные, испытательные и в качестве пе­реносчика (несущей) для получения модулированных сигналов.

Строго говоря, детерминированных сигналов в природе не су­ществует. Из-за многочисленных внешних и внутренних воздей­ствий на источник (генератор) сигналов их форма непредсказу­емо изменяется. Реальные сигналы и помехи всегда случайны.

Случайным называется сигнал, математическим описанием ко­торого является случайная функция времени. Физически сигнал можно считать случайным, если невозможно определенно пред­сказать или вычислить его мгновенные значения. Помехи системы связи чаще всего являются случайными. Сигналы же, в зависимо­сти от обстоятельств, могут быть и детерминированными,,и слу­чайными. Случайные сигналы не обязательно являются сложны­ми, они могут быть и простыми. Например, на выходе кодера по­лучаем случайную последовательность прямоугольных импульсов, отображающую случайную последовательность букв на входе.

Необходимо отметить, что только случайные сигналы являют­ся переносчиками информации. По определению, информация — это какие-то новые сведения для получателя. А в детерминиро­ванном сигнале этих новых сведений нет, сигнал полностью изве­стен. Нет новых сведений — нет и информации.

Свойства случайных сигналов, базирующиеся на математиче­ском аппарате теории вероятностей, приведены в § 2.5.

Непрерывные, дискретные и цифровые сигна-л ы. Любой физический процесс формирования сообщений и со­ответствующих им сигналов, в сущности, протекает так, что в лю­бой момент можно измерить значение сигналов. Сигналы, суще­ствующие непрерывно во времени и принимающие любые значе­ния из какого-то интервала, принято называть непрерывными, или аналоговыми (рис. 2.5,а).

Первоначально,в электросвязи использовались преимуществен­но аналоговые сигналы. Их можно просто генерировать, усили­вать, передавать и принимать. Недостатком таких сигналов явля­ется то, что любое изменение их формы из-за помех и искажений влечет за собой изменение формы принимаемого сообщения. Воз­росшие требования к точности воспроизведения сообщений заста­вили перейти к дискретным и цифровым сигналам.

Дискретные сигналы — это сигналы, принимающие конечное число значений или состояний. Дискретные сигналы могут непо­средственно создаваться на выходе преобразователя сообщение — сигнал или образовываться в результате дискретизации аналого­вых сигналов. Здесь следует различать дискретизацию по време­ни и по уровню.

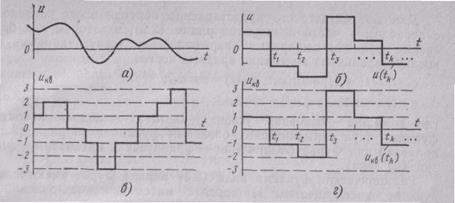
Рис. 2.5. Сигналы:

а—непрерывные; б - дискретные по времени; в - квантованные по

уровню и непрерыв­ные по времени; г - квантованные по уровню и

дискретные по времени

На рис. 2.5,6 изображен сигнал, заданный в дискретные мо­менты t_к Значения сигнала в точках t_к (отсчетные значения) u(t_к) такие же, как и в аналоговом сигнале. Такой сигнал назы­вают дискретным по времени. Обычно шаг дискретизации Dt_к= t_к- t_к-1 выбирают постоянным.

Можно произвести дискретизацию сигнала не по времени, а по уровню (рис. 2.5,в). Здесь сигнал непрерывный по времени но принимает только конечное число значений по уровню. Чтобы отличить эту процедуру от предыдущей, принято дискретизацию сигнала по уровню называть квантованием.

В принципе, можно осуществить для одного и того же сигна­ла и дискретизацию по времени, и квантование по уровню (рис.2.5,г), получая квантованные отсчетные значения сигнала u_кв(t_к)

Цифровые сигналы — разновидность дискретных сигналов когда квантовые отсчетные значения представлены в виде цифр. Цифровыми также являются сигналы, соответствующие ко довым комбинациям на выходе кодера. Преимущество цифровых сигналов — более высокая помехоустойчивость и возможность их формирования и обработки микроэлектронными логическими уст­ройствами. Цифровые сигналы находят все большее применение в новых системах электросвязи.