2015-05-30
425
Сплайновые поверхности
Напомним некоторые понятия.
Регулярной поверхностью называется множество точек М(х, у, z) пространства, координаты х, у, z которых определяются из соотношений
x = x(u,v), y = y(u,v), z = z(u,v), (u,v)ÎD, (11)
гдe x(u,v), y(u,v), z(u,v) - гладкие функции своих аргументов, причем выполнено соотношение
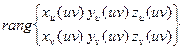= 2
D - некоторая область на плоскости параметров u и v. Последнее равенство означает, что в каждой точке регулярной поверхности существует касательная плоскость и положение нормали к этой плоскости при непрерывном перемещении по поверхности текущей точки изменяется непрерывно (рис. 20). Уравнения (11) называются параметрическими уравнениями поверхности. Их часто записывают также в векторной форме:
r = r(u,v), (u,v)ÎD,
где
r(u, v) = (x(u, v), y(u,v), z(u,v)).
Будем считать для простоты, что область на плоскости параметров представляет собой стандартный единичный квадрат (рис. 21).
Ограничим наши рассмотрение наборами точек вида
Vij, i = 0, I,..., m;,j = 0, 1,..., n.
Соединяя соответствующие вершины прямолинейными отрезками, получаем контрольный многогранник (точнее, контрольный, или опорный, граф) заданного массива V (рис. 22).
Сглаживающая поверхность строится относительно просто, в виде так называемого тензорного произведения. Так принято называть поверхности, описываемые параметрическими уравнениями вида
,
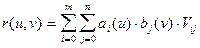где a £ u £ b, g £ v £ d
То обстоятельство, что приведенное выше уравнение можно записать в следующей форме:
,
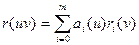где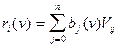 
i = 0,...,m, j = 0,...,n,
позволяет переносить на двумерный случай многие свойства, результаты и наблюдения, полученные при исследовании кривых. Если при проводимом обобщении не сильно отклоняться от рассмотренных выше классов кривых, то так построенные поверхности будут "наследовать" многие свойства одноименных кривых. В этом бесспорное преимущество задания поверхности в виде тензорного произведения.
