Отметки внутренних состояний автомата Мили по закодированной ГСА выполняются по следующим правилам:
1. символом 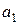 отмечается вход первой вершины, следующей за начальной, а также вход конечной вершины;
отмечается вход первой вершины, следующей за начальной, а также вход конечной вершины;
2. входы вершин, следующих за операторными вершинами, отмечаются символами 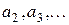 ;
;
3. входы двух различных вершин, за исключением конечной, не могут быть отмечены одинаковыми символами;
4. вход вершины может отмечаться только одним символом.
Внутренние состояния автомата Мили отмечены на дугах ГСА (рис. 5.7).
Прямой структурной таблицей микропрограммного автомата назовем таблицу, в которой последовательно перечисляются вначале все переходы из первого состояния в другие состояния, затем из второго состояния в другие и так далее.
Структурные таблицы по существу задают граф переходов автомата в виде списка, что является более компактной, но менее наглядной формой задания закона функционирования автомата.
Прямой структурной таблицей автомата Мили для ГСА на рис. 5.7 является таблица 5.1
|
|
|
Таблица 5.1 – Прямая структурная таблица для автомата Мили
В таблице 5.1 h -указывает номер строки; 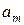 – исходное состояние автомата для такта t;
– исходное состояние автомата для такта t; 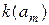 – двоичный код состояния
– двоичный код состояния 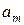 ;
; 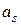 – состояние перехода для момента времени t+1;
– состояние перехода для момента времени t+1; 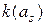 – двоичный код состояния перехода;
– двоичный код состояния перехода; 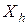 – условие перехода для строки h;
– условие перехода для строки h; 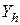 – выходной сигнал на переходе из
– выходной сигнал на переходе из 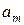 в
в 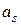 для строки h;
для строки h; 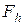 – сигналы возбуждения входов триггеров.
– сигналы возбуждения входов триггеров.
Следует отметить, что по сравнению с таблицами переходов и выходов цифрового автомата Мили структурная таблица является их расширением, так как содержит три дополнительных столбца 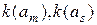 и
и 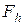 . Столбец h может отсутствовать в таблице, но его присутствие позволяет осуществить нумерацию переходов и облегчает анализ таблиц. Столбцы
. Столбец h может отсутствовать в таблице, но его присутствие позволяет осуществить нумерацию переходов и облегчает анализ таблиц. Столбцы 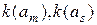 и
и 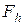 окончательно оформляются после выполнения этапа кодирования внутренних состояний автомата.
окончательно оформляются после выполнения этапа кодирования внутренних состояний автомата.
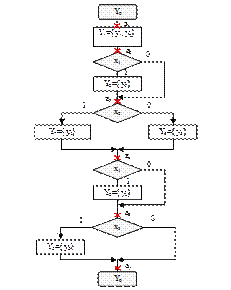
Рисунок 5.7 – Разметка ГСА по Типу автомата Мили
Структурная таблица автомата по существу является списочной формой (списком) представления графа переходов автомата, но более компактна по сравнению с ним.
В ряде случаев, оказывается более удобным пользоваться обратной структурной таблицей автомата (таблица 5.2), в которой столбцы обозначены точно также, но сначала записываются все переходы в 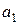 , затем в
, затем в 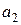 и так далее. Таким образом, в прямой структурной таблице автомата Мили ведущим является столбец
и так далее. Таким образом, в прямой структурной таблице автомата Мили ведущим является столбец 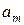 , в обратной таблице ведущим является столбец
, в обратной таблице ведущим является столбец 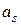 .
.
Таблица 5.2– Обратная структурная таблица для автомата Мили
Теперь построим граф переходов для автомата Мили по табл. 5.2 или 5.1. Каждая строка таблицы соответствует дуге графа (рис.5.8).
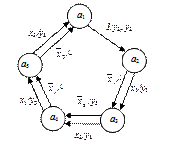
Рисунок 5.8 – Граф переходов автомата Мили
|
|
|
Каждое состояние автомата должно быть как-то представлено в схеме, где-то храниться. Состояние кодируется двоичной последовательностью, которая хранится в триггерах. Каждому новому состоянию соответствует своя уникальная двоичная последовательность, чтобы состояния были различимыми.
Минимальное число триггеров для хранения состояний, определяется выражением
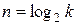 ,
,
где n – число триггеров для хранения состояний;
k – количество состояний.
Как кодировать состояния? Существует большое количество методов кодирования, о которых речь пойдет позже. Сейчас рассмотрим алгоритм кодирования состояний, при условии использования D-триггеров. Целью такого кодирования будет минимизация сложности схемы, т.е. минимизация аппаратурных затрат.
Для уменьшения сложности системы, реализующей функции возбуждения D-триггеров лучше использовать частотный алгоритм кодирования состояний автомата. Этот алгоритм состоит из 5-ти этапов.
1. Каждому внутреннему состоянию автомата аi ставится в соответствие целое число Ni, равное числу переходов в это состояние (Ni равно числу появлений состояния аi в таблице переходов или числу стрелок, входящих в аi в графе переходов).
2. Все числа N1, N2,… Ni,… NМ сортируются по убыванию.
3. Состояние at с максимальным значением Nt кодируется нулевой комбинацией, т.е. кодом kt=00…00;
4. Следующие n внутренних состояний кодируются кодовой комбинацией с одной единицей: 00…01, 00…10,…
5. Оставшиеся незакодированные внутренние состояния кодируют вначале комбинациями с двумя единицами, затем с тремя и т. д., пока все состояния не будут закодированы.
В результате получаем такое кодирование, при котором чем больше имеется переходов в некоторое состояние, тем меньше единиц содержится в его коде.
Подобные соображения могут быть использованы при кодировании выходных сигналов для минимизации функции выходов.
Кодирование состояний по выше рассмотренному алгоритму сведено в табл. 5.3
Таблица 5.3– Кодирование состояний автомата Мили на D -триггерах
| D 3 D 2 D 1 | ||
| a1 – 2 a2 – 1 a3 – 2 a4 – 2 a5 – 2 | a1 – 2 a3 – 2 a4 – 2 a5 – 2 a2 – 1 |
Граф переходов с закодированными состояниями приведен на рис. 5.9. На дугах графа указаны разряды, на которые имеются единицы кодов состояний, куда входят дуги.
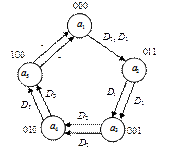
Рисунок 5.9 – Кодирование состояний автомата Мили
Коэффициент качества кодирования определяется как отношение числа букв D на графе к общему числу дуг.
Заполненная прямая структурная таблица для автомата Мили представлена в табл. 5.4.
Таблица 5.4 – Прямая структурная таблица для автомата Мили
| h | 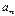
| 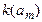
| 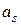
| 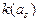
| 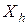
| 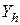
| 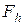 D 3 D 2 D 1
D 3 D 2 D 1
|
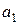
| 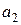
| 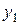 , , 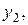
| |||||
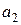
| 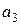
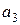
| 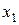
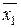
| 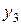 –
–
| ||||
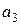
| 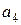
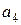
| 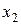
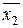
| 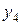
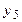
| ||||
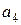
| 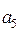
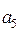
| 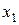
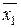
| 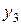 –
–
| ||||
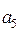
| 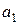
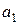
| 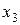
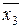
| 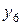 –
–
|
Функции возбуждения Zк и функция выхода Yl автомата Мили находят по полностью оформленной структурной таблице автомата в виде дизъюнктивных нормальных форм:
Zк = V аm·Хh (аm,аs); к = 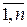 ,
,
(аm,аs) Î h;
Yl = V аm · Хh (аm,аs); l = 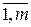 ,
,
(am,as) Î h,
где n и m – число сигналов возбуждения и исходных сигналов автомата соответственно; h – номер строки структурной таблицы, в столбце F (аm, аs) которой есть отметка сигнала возбуждения ZК или в столбце Y (аm, аs) - отметка исходного сигнала Yl. Терм (логическое произведение) аm Хh (аm, аs) включают в выражение Zк, если сигнал возбуждения Zк есть в столбце F (аm, аs) h -й строки таблицы автомата Мили.
Аналогично терм аm Xh (am, as) нужно включить в выражение Yl, если Yl есть в столбце Y (am,as) h -й строки таблицы.
Функции выходов, исходя из таблицы 5.4, в базисах Буля и Шеффера будут иметь следующий вид:
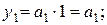
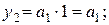
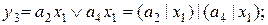
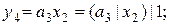
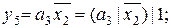
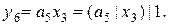
Функции переходов, исходя из таблицы 5.4, в базисах Буля и Шеффера будут иметь следующий вид:
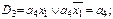
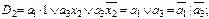
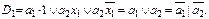
Далее можно строить функциональную электрическую схему автомата.
|
|
|
Рассмотрим реализацию схемы с преддешифрацией. В данном случае будем для формирования одноразрядного сигнала состояния использовать дешифратор, который будет преобразовывать двоичный код состояния в двоичный унитарный код, т.е. код, в котором только один сигнал будет активным, он и будет указывать на состояние, в котором находится автомат в течении рассматриваемого такта.
Для построения функциональной электрической схемы необходимо написать еще одно уравнение для формирования синхросигнала. Для этого предусмотрим сигнал запуска z, активное значение которого будет инициировать подачу синхросигнала C на элементы памяти. Уравнение имеет вид:
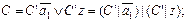
где z – сигнал запуска,
C – сигнал синхронизации, подаваемый на схему,
C ’ – сигнал синхронизации с генератора тактовых сигналов.
Кроме того, необходимо предусмотреть установку элементов памяти в начальное состояние по включению питания. Для этого понадобятся две простые схемы, представленные на рис. 5.10 а и б.
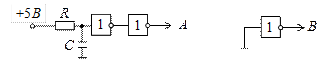
а) б)
Рисунок 5.10 – Схемы сигналов установки триггеров в начальное состояние
На рис. 5.11 представлены временные диаграммы сигнала напряжения на обкладках конденсатора С, и сигналов А и В с выходов схем установки триггеров.
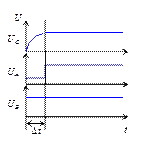
Рисунок 5.11 – Временные диаграммы сигналов А, В и UC
Пока конденсатор заряжается, на выходе А держится значение 0, так называемый вынужденный 0. На выходе В – постоянное значение 1. В период D t вынужденного нуля держится комбинация А = 0, В = 1. После зарядки конденсатора появляется комбинация А = 1, В = 1. Подключая сигналы А и В к установочным входам триггера. Можно обеспечить его установку в 0 (рис. 5.12 а) или его установку в 1 (рис. 5.12 б) по включению питания. В обоих случаях после зарядки конденсатора устанавливается комбинация А = 1, В = 1, которая позволяет триггеру нормально функционировать.
 Рисунок 2.11 – Схема буфера
Инвертор и буфер могут использоваться для формирования константных (постоянных) значений 0 и1 (рис.2.12).
Рисунок 2.11 – Схема буфера
Инвертор и буфер могут использоваться для формирования константных (постоянных) значений 0 и1 (рис.2.12).
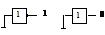 Рисунок 2.12– Схемы реализации константных 0 и 1
Элемент И-НЕ (функция Шеффера, образующая функционально полный базис) представлен на рис. 2.1.3.
Рисунок 2.12– Схемы реализации константных 0 и 1
Элемент И-НЕ (функция Шеффера, образующая функционально полный базис) представлен на рис. 2.1.3.
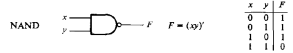 Рисунок 2.13 – Элемент И-НЕ
Рассмотрим некоторые свойства функции Шеффера (2.1).
Рисунок 2.13 – Элемент И-НЕ
Рассмотрим некоторые свойства функции Шеффера (2.1).
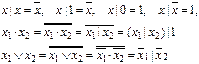 Элемент ИЛИ-НЕ (функция Пирса (Вебба), образующая функционально полный базис) представлен на рис. 2.1.8.
Элемент ИЛИ-НЕ (функция Пирса (Вебба), образующая функционально полный базис) представлен на рис. 2.1.8.
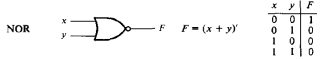 Рисунок 2.18 – Элемент ИЛИ-НЕ
Рассмотрим некоторые свойства функции Шеффера (2.4).
Рисунок 2.18 – Элемент ИЛИ-НЕ
Рассмотрим некоторые свойства функции Шеффера (2.4).
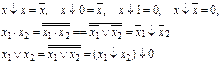 Существую еще два стандартных логических вентиля.
Элемент исключающее ИЛИ представлен на рис. 2.24. Он реализует операцию суммы по модулю два.
Существую еще два стандартных логических вентиля.
Элемент исключающее ИЛИ представлен на рис. 2.24. Он реализует операцию суммы по модулю два.
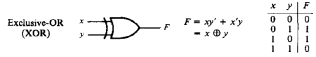 Рисунок 2.24 – Элемент исключающее ИЛИ
Элемент исключающее ИЛИ с инверсией представлен на рис. 2.25. Он реализует операцию отрицания суммы по модулю два (эквивалентность).
Рисунок 2.24 – Элемент исключающее ИЛИ
Элемент исключающее ИЛИ с инверсией представлен на рис. 2.25. Он реализует операцию отрицания суммы по модулю два (эквивалентность).
 Рисунок 2.25 – Элемент эквивалентность
5. Ассоциативность функций И (AND), ИЛИ (OR), И-НЕ (NAND) ИЛИ-НЕ (NOR), XOR, XNOR.
Элемент И-НЕ. Закон коммутативности выполняется, а ассоциативности – нет. Невыполнение ассоциативности проиллюстрируем ниже (выражение 2.2 и рис. 2.14).
Рисунок 2.25 – Элемент эквивалентность
5. Ассоциативность функций И (AND), ИЛИ (OR), И-НЕ (NAND) ИЛИ-НЕ (NOR), XOR, XNOR.
Элемент И-НЕ. Закон коммутативности выполняется, а ассоциативности – нет. Невыполнение ассоциативности проиллюстрируем ниже (выражение 2.2 и рис. 2.14).
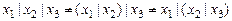 Истинность выражения (2.2) демонстрируется выражениями (2.3).
Истинность выражения (2.2) демонстрируется выражениями (2.3).
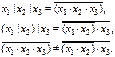 В схемной реализации это проиллюстрировано на рис. 2.14.
В схемной реализации это проиллюстрировано на рис. 2.14.
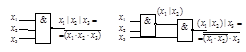 Рисунок 2.14 – Иллюстрация невыполнимости ассоциативности в базисе Шеффера
Для функции И базиса Буля ассоциативность иллюстрируется рис. 2.15. Каскадное соединение двух двухвходовых вентилей эквивалентно одному трехвходовому
.
Рисунок 2.14 – Иллюстрация невыполнимости ассоциативности в базисе Шеффера
Для функции И базиса Буля ассоциативность иллюстрируется рис. 2.15. Каскадное соединение двух двухвходовых вентилей эквивалентно одному трехвходовому
. 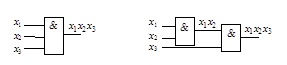 Рисунок 2.15 – Иллюстрация выполнимости ассоциативности в базисе Буля
Рассмотрим переход от базиса Буля к базису Шеффера. Функция в базисе Буля может быть представлена в любой форме, в том числе и в канонической (в виде ДНФ или КНФ). Следующая функция записана в виде ДНФ.
Рисунок 2.15 – Иллюстрация выполнимости ассоциативности в базисе Буля
Рассмотрим переход от базиса Буля к базису Шеффера. Функция в базисе Буля может быть представлена в любой форме, в том числе и в канонической (в виде ДНФ или КНФ). Следующая функция записана в виде ДНФ.
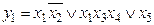 Вне зависимости от представления функции для перехода к базису Шеффера необходимо поставить над выражением двойное отрицание и выполнять преобразования по законам де Моргана.
Вне зависимости от представления функции для перехода к базису Шеффера необходимо поставить над выражением двойное отрицание и выполнять преобразования по законам де Моргана.
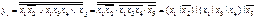 На рис. 2.16 представлена схемная реализация функции
На рис. 2.16 представлена схемная реализация функции 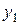 в базисе Буля
в базисе Буля
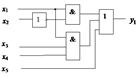 Рисунок 2.16 – Схемная реализация функции
Рисунок 2.16 – Схемная реализация функции 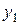 в базисе Буля
На рис. 2.17 представлена схемная реализация функции
в базисе Буля
На рис. 2.17 представлена схемная реализация функции 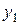 в базисе Шеффера
в базисе Шеффера
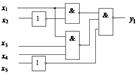 Рисунок 2.17 – Схемная реализация функции
Рисунок 2.17 – Схемная реализация функции 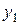 в базисе Шеффера
Сформулируем правило перехода от ДНФ к уравнению в базисе Шеффера. При переходе от ДНФ к уравнению в базисе Шеффера все термы (элементарные коньюнкции) заключаются в скобки, а все знаки коньюнкций и дизьюнкций заменяются на знак операции Шеффера. Над однобуквенными термами ставятся знаки отрицания.
ИЛИ-НЕ. Закон коммутативности выполняется, а ассоциативности – нет. Невыполнение ассоциативности проиллюстрируем ниже (выражение 2.5 и рис. 2.19).
в базисе Шеффера
Сформулируем правило перехода от ДНФ к уравнению в базисе Шеффера. При переходе от ДНФ к уравнению в базисе Шеффера все термы (элементарные коньюнкции) заключаются в скобки, а все знаки коньюнкций и дизьюнкций заменяются на знак операции Шеффера. Над однобуквенными термами ставятся знаки отрицания.
ИЛИ-НЕ. Закон коммутативности выполняется, а ассоциативности – нет. Невыполнение ассоциативности проиллюстрируем ниже (выражение 2.5 и рис. 2.19).
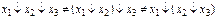 (2.5)
Истинность выражения (2.5) демонстрируется выражениями (2.6).
(2.5)
Истинность выражения (2.5) демонстрируется выражениями (2.6).
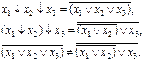 (2.6)
В схемной реализации это проиллюстрировано на рис. 2.19.
(2.6)
В схемной реализации это проиллюстрировано на рис. 2.19.
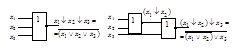 Рисунок 2.19 – Иллюстрация невыполнимости ассоциативности в базисе Пирса
Для функции ИЛИ базиса Буля ассоциативность иллюстрируется рис. 2.20. Каскадное соединение двух двухвходовых вентилей эквивалентно одному трехвходовому.
Рисунок 2.19 – Иллюстрация невыполнимости ассоциативности в базисе Пирса
Для функции ИЛИ базиса Буля ассоциативность иллюстрируется рис. 2.20. Каскадное соединение двух двухвходовых вентилей эквивалентно одному трехвходовому.
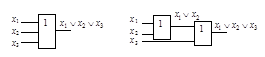 Рисунок 2.20 – Иллюстрация выполнимости ассоциативности в базисе Буля
Рассмотрим переход от базиса Буля к базису Пирса. Функция в базисе Буля может быть представлена в любой форме, в том числе и в канонической (в виде ДНФ или КНФ). Следующая функция записана в виде КНФ.
Рисунок 2.20 – Иллюстрация выполнимости ассоциативности в базисе Буля
Рассмотрим переход от базиса Буля к базису Пирса. Функция в базисе Буля может быть представлена в любой форме, в том числе и в канонической (в виде ДНФ или КНФ). Следующая функция записана в виде КНФ.
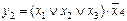 Вне зависимости от представления функции для перехода к базису Пирса необходимо поставить над выражением двойное отрицание и выполнять преобразования по законам де Моргана.
Вне зависимости от представления функции для перехода к базису Пирса необходимо поставить над выражением двойное отрицание и выполнять преобразования по законам де Моргана.
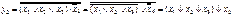 На рис. 2.21 представлена схемная реализация функции
На рис. 2.21 представлена схемная реализация функции 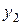 в базисе Буля
в базисе Буля
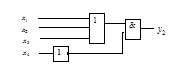 Рисунок 2.21 – Схемная реализация функции
Рисунок 2.21 – Схемная реализация функции 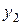 в базисе Буля
На рис. 2.22 представлена схемная реализация функции
в базисе Буля
На рис. 2.22 представлена схемная реализация функции 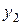 в базисе Пирса
в базисе Пирса
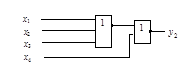 Рисунок 2.22 – Схемная реализация функции
Рисунок 2.22 – Схемная реализация функции 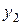 в базисе Пирса
Сформулируем правило перехода от КНФ к уравнению в базисе Пирса. При переходе от КНФ к уравнению в базисе Пирса все термы (элементарные дизьюнкции) заключаются в скобки, а все знаки коньюнкций и дизьюнкций заменяются на знак операции Пирса. Над однобуквенными термами ставятся знаки отрицания.
Рассмотрим переход от ДНФ к базису Пирса на примере функции
в базисе Пирса
Сформулируем правило перехода от КНФ к уравнению в базисе Пирса. При переходе от КНФ к уравнению в базисе Пирса все термы (элементарные дизьюнкции) заключаются в скобки, а все знаки коньюнкций и дизьюнкций заменяются на знак операции Пирса. Над однобуквенными термами ставятся знаки отрицания.
Рассмотрим переход от ДНФ к базису Пирса на примере функции 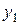 . Для этого необходимо поставить двойные отрицания над всеми термами и над выражением в целом, раскрывая их по правилу де Моргана.
. Для этого необходимо поставить двойные отрицания над всеми термами и над выражением в целом, раскрывая их по правилу де Моргана.
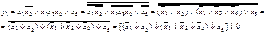 В результате получается менее экономичная с точки зрения аппаратурных затрат реализация, поскольку появляется дополнительная ступень в виде двухвходового элемента, необходимая для реализации инверсии (входные инверсии обычно не учитываются). Это проиллюстрировано на рис. 2.23.
В результате получается менее экономичная с точки зрения аппаратурных затрат реализация, поскольку появляется дополнительная ступень в виде двухвходового элемента, необходимая для реализации инверсии (входные инверсии обычно не учитываются). Это проиллюстрировано на рис. 2.23.
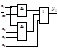
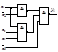
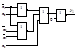 Рисунок 2.23 – Схемная реализация функции
Рисунок 2.23 – Схемная реализация функции 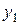 в базисах Буля (а), Шеффера (б) и Пирса (в)
Аналогично выполняется переход от КНФ к Базису Шеффера (выполнить самостоятельно на примере функции
в базисах Буля (а), Шеффера (б) и Пирса (в)
Аналогично выполняется переход от КНФ к Базису Шеффера (выполнить самостоятельно на примере функции 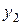 ).
Для функции XOR ассоциативность иллюстрируется рис. 2.26. Каскадное соединение двух двухвходовых вентилей эквивалентно одному трехвходовому. Справедливость этого высказывания можно проверить, составив две таблицы истинности (выполнить самостоятельно).
).
Для функции XOR ассоциативность иллюстрируется рис. 2.26. Каскадное соединение двух двухвходовых вентилей эквивалентно одному трехвходовому. Справедливость этого высказывания можно проверить, составив две таблицы истинности (выполнить самостоятельно).
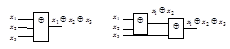 Рисунок 2.26 – Иллюстрация выполнимости ассоциативности XOR
Для функции XNOR ассоциативность не выполняется. Это иллюстрируется рис. 2.27. Каскадное соединение двух двухвходовых вентилей не эквивалентно одному трехвходовому. Справедливость этого высказывания можно проверить, составив две таблицы истинности (выполнить самостоятельно).
Рисунок 2.26 – Иллюстрация выполнимости ассоциативности XOR
Для функции XNOR ассоциативность не выполняется. Это иллюстрируется рис. 2.27. Каскадное соединение двух двухвходовых вентилей не эквивалентно одному трехвходовому. Справедливость этого высказывания можно проверить, составив две таблицы истинности (выполнить самостоятельно).
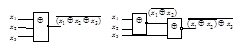 Рисунок 2.27 – Иллюстрация невыполнимости ассоциативности XNOR
На рис. 2.28 приведены временные диаграммы последних четырех рассмотренных стандартных логических элементов.
Рисунок 2.27 – Иллюстрация невыполнимости ассоциативности XNOR
На рис. 2.28 приведены временные диаграммы последних четырех рассмотренных стандартных логических элементов.
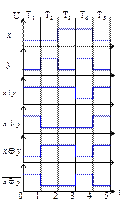 Рисунок 2.28 – Временные диаграммы
8. Операции кубического исчисления пересечение, объединение и дополнение
Операции кубического исчисления определяют преобразования над выражениями в кубической (векторной форме) в алфавите {0, 1, X}. Основными теоретико-множественными операциями кубического исчисления являются пересечение, объединение и дополнение. Существует еще ряд специальных теоретико-множественных кубических операций, используемых в кубических методах минимизации булевых функций, для моделирования и построения тестов при описании примитивных элементов схем в кубическом виде, но они используются достаточно редко и не рассматриваются в данном курсе.
Операция пересечения (Ç) двух n-мерных векторов (кубов) А = (а1,а2,... аn) и B = (b1,b2,... bn), где n - количество разрядов вектора (координат куба), обозначается C = A Ç B, где C = (c1,c2,... cn), и определяется следующим образом:
Рисунок 2.28 – Временные диаграммы
8. Операции кубического исчисления пересечение, объединение и дополнение
Операции кубического исчисления определяют преобразования над выражениями в кубической (векторной форме) в алфавите {0, 1, X}. Основными теоретико-множественными операциями кубического исчисления являются пересечение, объединение и дополнение. Существует еще ряд специальных теоретико-множественных кубических операций, используемых в кубических методах минимизации булевых функций, для моделирования и построения тестов при описании примитивных элементов схем в кубическом виде, но они используются достаточно редко и не рассматриваются в данном курсе.
Операция пересечения (Ç) двух n-мерных векторов (кубов) А = (а1,а2,... аn) и B = (b1,b2,... bn), где n - количество разрядов вектора (координат куба), обозначается C = A Ç B, где C = (c1,c2,... cn), и определяется следующим образом:
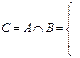
| Æ если aiÇbi=Æ хотя бы для одной из координат пересекаемых кубов, i=1,n; ((a1Çb1), (a2Çb2),... (anÇbn)) в противном случае. |
Кубическая операция пересечения является покоординатной (т.е. ее результат определяется для каждой координаты независимо) и правила ее выполнения в каждом разряде указаны в таблице 2.1. Отметим, что ранг результата пересечения С всегда меньше или равен рангу меньшего из кубов, участвующих в пересечении.
|
|
|
Таблица 2.1 - Кубическая операция пересечения
| Ç | X | ||
| Æ | |||
| Æ | |||
| X | X |
Частным случаем операции пересечения является операция поглощения (Î). Часто в литературе эту операцию называют операцией принадлежности по аналогии с соответствующей теоретико-множественной операцией. Куб А поглощается кубом В (А принадлежит В) (А Î В), если А Ç В = А. Если в поглощении участвуют одинаковые кубы, то результатом будет один из этих кубов.
Ниже приведены примеры выполнения операции пересечения C = A Ç B для различных операндов.
0X0X Ç X10X = 010X;
0X0X Ç 110X = Æ;
0X00 Ç 0X0X = 0X00 (поглощение, A Î B);
0X01 Ç 0X01 = 0X01 (A = B).
Операция объединения (È) двух n-мерных кубов А = (а1,а2,... аn) и B = (b1,b2,... bn), где n - количество координат куба, обозначается C = A È B, где C = (c1,c2,... cn), и определяется как C = ((a1Èb1), (a2È2),... (anÈbn)). Кубическая операция объединения является покоординатной и правила ее выполнения в каждом разряде указаны в таблице в таблице 2.2. Ранг результата объединения С всегда больше или равен рангу большего из кубов, участвующих в объединении. Отметим, что для кубов с кодовым расстояним d больше или равным 2, результаты объединения могут быть противоречивыми.
Таблица 2.2 - Кубическая операция объединения
| È | X | ||
| X | X | ||
| X | X | ||
| X | X | X | X |
Частным случаем операции объединения является операция склеивания. Кубы одного ранга А и В склеиваются, если они различаются только в одном разряде i, причем ai и bi не равны X. Отметим, что именно операция склеивания никогда не дает противооречивых результатов.
Ниже приведены примеры выполнения операции объединения C = A È B для различных операндов.
0X0X È 0XX0 = 0XXX (d=2, результат противоречив, т.к. 0X11 ÏA,B, но 0X11 Î0XXX);
0X0X È 0X01 = 0X0X (поглощение, B ÎA);
0X01 È 0X00 = 0X0X (d=1, склеивание);
0101 È 0110 = 01XX (d=2, результат противоречив).
Операция дополнения для одного n-мерного куба А = (а1,а2,... аn), где n - количество координат куба, обозначается C = Ā, где C = (c1,c2,... cn). По аналогии с аналитическим описанием логических функций операцию дополнения часто называют логической инверсией и правила ее выполнения в каждом разряде указаны в табл. 2.3. Отметим, что ранг дополнения С по отношению к исходному кубу А всегда остается неизменным.
Таблица 2.3 - Кубическая операция дополнения
| А | X | ||
| C = Ā | X |
Примеры выполнения
A = 0X0X, C = 1X1X;
A = 0110, C = 1001.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
|
|

 2015-05-30
2015-05-30 1549
1549







