Нормальное распределение. Показательное распределение

Непрерывная случайная величина X называется распределенной по нормальному закону, если ее плотность распределения вероятности имеет вид:

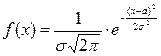, где 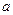- математическое ожидание и 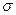- средне квадратическое отклонение – параметры нормального распределения.

Нормальное распределение еще называют распределением Гаусса.

Примеры нормально распределенных случайных величин:

1) размеры механически обрабатываемых деталей;

2) ошибки всевозможных приборов;

3) производительность труда;

4) урожайность с/х культуры с 1га.

График плотности вероятности для нормального распределения представляет собой колокол-образную кривую; при этом параметр “a” соответствует точке максимума, через которую проходит ось симметрии, а параметр “ 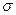” – расстоянию от этой оси до точки перегиба.

Вероятность того, что случайная величина X, распределенная по нормальному закону, примет значение, принадлежащее интервалу 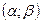, вычисляется по формуле:

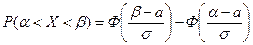, где

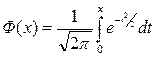- функция Лапласа, значения которой находятся по специальным таблицам в приложениях к учебникам.

Замечание 1. Особый интерес представляет частный случай: c какой вероятностью отклонение значений случайной величины X от математического ожидания по абсолютной величине не превосходит заданной величины :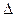

.

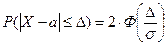Замечание 2. Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения. Такое событие происходит почти наверняка (правило “трех сигм”):

.

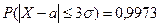Свойства:

1. Областью определения функции f(x) является вся числовая ось;

2. Функция f{x) может принимать только положительные значения, т. е. f(x}>0;

3. Предел функции f(x) при неограниченном возрастании |х| равен нулю, т. е. ось ОХ является горизонтальной асимптотой графика функции;

4°. Функция f{x) имеет в точке х = a максимум, равный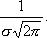

5. График функции f(x) симметричен относительно прямой х = а.

6. Нормальная кривая в точках х = а +s имеет перегиб,

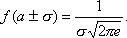
На основании доказанных свойств построим график плотности нормального распределения f(x).

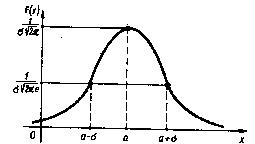
Как видно из рисунка, нормальная кривая имеет колоколообразную форму. Эта форма является отличительной чертой нормального распределения. Иногда нормальную кривую называют кривой Гаусса.

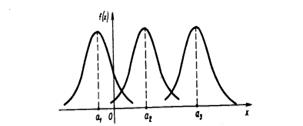
При изменении параметра а форма нормальной кривой не изменяется. В этом случае, если математическое ожидание (параметр а) уменьшилось или увеличилось, график нормальной кривой сдвигается влево или вправо.

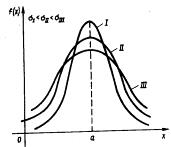
При изменении параметра s изменяется форма нормальной кривой. Если этот параметр увеличивается, то максимальное значение функции f(x) убывает, и наоборот. Так как площадь, ограниченная кривой распределения и осью Ох, должна быть постоянной и равной 1, то с увеличением параметра кривая приближается к оси Ох и растягивается вдоль нее, а с уменьшением s кривая стягивается к прямой х=а.

Использование формул f(x) и F(x) для практических расчетов затруднительно. Но решение задач по этим формулам можно упростить, если от нормального распределения с произвольными параметрами а и s перейти к нормальному распределению с параметрами а=0, s = 1.

Функция плотности нормального распределения f(x) с параметрами а=0, s =1 называется плотностью стандартной нормальной случайной величины и ее график имеет вид:

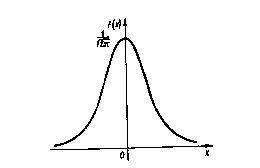
Функция плотности и интегральная функция стандартной нормальной СВ будут иметь вид:

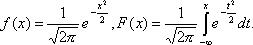
Для вычисления вероятности попадания СВ в интервал (a, b) воспользуемся функцией Лапласа:

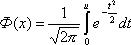
Перейдем к стандартной нормальной случайной величине

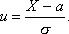
Тогда

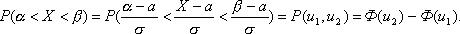
Пример 16. Длина X изготавливаемой автоматом детали представляет собой случайную величину, распределенную по нормальному закону с параметрами 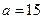см, 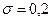см. Найти вероятность брака, если допустимые размеры детали должны быть 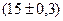см.

Решение. Требуется найти 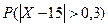- вероятность брака. Сначала находим вероятность изготовления качественной детали, используя формулу (18):

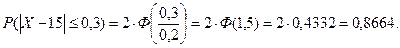Тогда искомая вероятность равна:

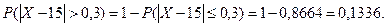
Ответ: 0,1336.