Основные понятия. Множества, элементами которых являются точки, называются точечными

ВЫПУКЛЫЕ МНОЖЕСТВА ТОЧЕК

Множества, элементами которых являются точки, называются точечными. Примерами точечных множеств на плоскости являются: точки круга (или круг), точки прямой (или прямая), луч, отрезок, угол, сектор, треугольник и т. д.; в пространстве — шар, призма, паралле­лепипед, точки кольца в виде «бублика» и т.п.

Точечные множества (далее, говоря «множество», будем подразу­мевать только точечное множество) делятся на выпуклые и невыпук­лые.

Множество точек называется выпуклым, если вместе с его любыми двумя точками ему принадлежит и весь отрезок, соединяющий их. Если же существует хотя бы одна такая пара точек множества, что отрезок, соединяющий эти точки; не принадлежит целиком этому мно­жеству, то оно называется невыпуклым.

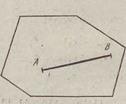
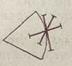
На рис. 1.1 изображено выпуклое множество (выпуклыймного­угольник), а на рис. 2.2 — невыпуклое.

Выпуклые множества обладают важным свойством, которое устанавливается следующей теоремой.

Теорема. Пересечение (общая часть) двух выпуклых множеств так­же выпуклое множество.

▼Пусть множества 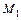и 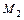— выпуклые (рис. 23). Если их пе­ресечение является пустым множеством или состоит только из одной точки, то справедливость теоремы очевидна, поскольку пустое

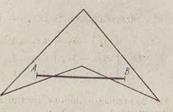
Рис. 1.1 Рис. 1.2

мно­жество и множество, состоящее из одной точки, — выпуклые. Поэтому полагаем, что пересечению принадлежат, по крайней мере, две точки. Пусть точки А и В — произвольные точки пересечения. Следователь­но, они принадлежат как множеству 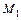, так и множеству 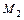. По­скольку, по условию, множества 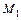и М ₂ — выпуклые, вместе с точ­ками А и В каждому из них принадлежат и все точки отрезка АВ.

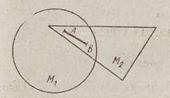
Рис. 1.3 Рис. 1.4

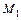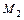Таким образом, пересечение множеств и вместе с его произволь­ными точками А и В содержит и все точки отрезка АВ, а поэтому оно является выпуклым множеством. ▲

Пользуясь методом математической индукции, можно доказать, что пересечение конечного числа выпуклых множеств также выпук­лое множество.

Частными случаями точечных множеств на плоскости служат вы­пуклые многоугольники (треугольники, прямоугольники, ромбы, тра­пеции, правильные многоугольники и т. д.), а в пространстве — выпуклые многогранники (призмы, пирамиды и т. д.)

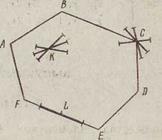
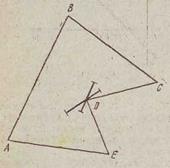
Через любую внутреннюю точку К выпуклого множества можно провести отрезок, для которого она является внутренней, а сам отре­зок целиком принадлежит этому множеству (рис. 1.4). Для гранич­ной точки 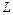, если границей множества является прямая или ее часть, также можно построить такойотрезок. В этом случае необходимо, чтобы этот отрезок принадлежал прямолинейному участку границы. Но есть точки (для выпуклого многоугольника — это его вершины), для кото-

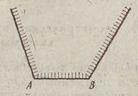
Рис. 1.5 Рис. 1.6

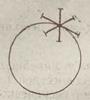
рых такое построение выполнить нельзя: нет ни одного отрезка, для которого вершина являлась бы внутренней, а отрезок целиком бы принадлежал многоугольнику (вершина С на рис. 1.4). Для точек отрезка АВ этим свойством обладают концы его А и В, для точек круга — все точки ограничивающей его окружности (рис. 1.5).

Точка выпуклого множества называется угловой (или крайней), если через нее нельзя провести ни одного отрезка, состоящего только

из точек данного множества и для которого она была бы внутренней.

Для выпуклого многоугольника уг­ло-выми точками являются все его вер­шины, для отрезка — его концы. Для полукруга все точки полуокружности — угловые. Вообще, любой граничный участок выпуклого множества, не являю­щийся прямой или ее частью, состоит только из угловых точек, т. е. их су­ществует бесконечное множество.

Рис. 1.7 Конечное число угловых точек на плоскости могут иметь лишь выпуклые множества, границами которых служат прямые или отрезки прямой, т. е. выпуклые многоугольники. Поэтому их можно определить как выпуклые множества точ1ек на плоскости с конечным числом угло­вых точек. В пространстве выпуклое множество с конечным чис­лом угловых точек называется выпуклым многогранником. В соответст­вии с этими определениями выпуклыми многоугольниками являются (рис. 1.6) не только треугольник, ромб, трапеция и т. д., но и точка, луч, угол (имеют по одной угловой точке), отрезок (имеет две угловые точки), прямая, вся плоскость, полуплоскость, часть плоскости, за­ключенная между двумя параллельными прямыми, включая эти прямые (не имеют угловых точек), и др. В трехмерном пространстве вы­пуклыми многогранниками являются пирамида, призма,параллеле­пипед и т. п., в 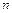-мерном пространстве — выпуклый многогранник. Понятие угловой точки вводится только для выпуклых множеств.Для невыпуклых множеств это определение теряет смысл. Например,на рис. 1.7 точка D — вершина невыпуклого многоугольника, а че­рез нее проведены отрезки, состоящие только из точек этого множест­ва, для которых она является внутренней.