Распределение числа успехов (появлений события) носит название биномиального распределения

Независимые испытания. Формула Бернулли При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли. Примеры повторных испытаний: 1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну; 2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой (роль пристрелки не учитывается).

7. Формула Бернулли.

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события А в единичном испытании буквой р, т.е 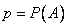, а вероятность противоположного события (событие А не наступило) - буквой 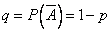Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли

Распределение числа успехов (появлений события) носит название биномиального распределения.

Наивероятнейшее число успехов Биномиальное распределение (распределение по схеме Бернулли) позволяет, в частности, установить, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов (появлений события) имеет вид: 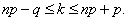Так как 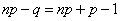то эти границы отличаются на 1. Поэтому k являющееся целым числом, может принимать либо одно значение, когда np целое число (k=np), то есть когда np+p (а отсюда и np-q) нецелое число, либо два значения, когда np-q целое число.

8. Локальная теорема Луавра-Лапласа.

Есл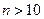и и 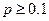, то используют локальную теорему Лапласа(6) Если число испытаний 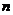велико, то пользоваться фор­мулой Бернулли не рационально, очень громоздко. Искомую вероятность при больших 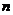можно вычислить по локальной теореме Лапласа, которая дает асимптоти­ческую формулу, позволяющую приближенно найти вероят­ность появления события в 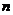испытаниях ровно 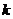раз.

Локальная теорема Лапласа: Если вероятность 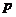появления события 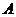в каждом испытании постоянна и отлич­на от 0 и 1, то вероятность 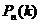того, что событие 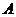появится в 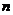испытаниях ровно к раз приближенно равна значению функции

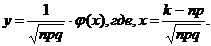
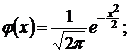
Значения функции 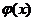находят по таблице (см. приложение 1). Функция 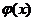четная, т.е. .

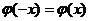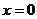
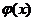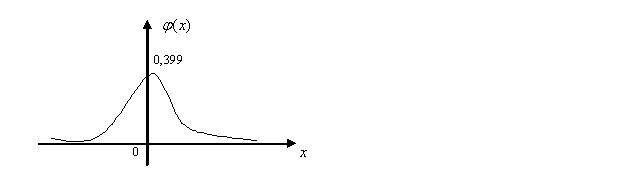
При достигает максимума, 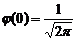= 0,399.

График функции 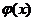называют кривой вероятностей.

Итак, вероятность того, что событие 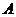появится в 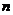независимых испытаниях ровно 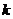раз, приближенно равна

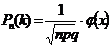, где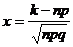

имеет следующие свойства: 1) φ(х)-четная; 2) точки перегиба х = ± 1; 3) при х≥5, φ(х)→0, поэтому функция φ(х) представлена в виде таблицы для 0≤х≤5

9. Формула Пуассона для массовых и редких явлений.

Есл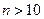и и 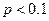, (либо 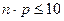) то используют формулу Пуассона Пусть производится 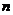независимых испытаний, в каждом из которых вероятность появления события 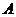равна 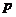. Для определения вероятности 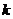появлений события в этих испытаниях используют формулу Бернулли. Если 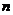велико, то пользуются асимптотической формулой Лапласа. Однако эти формулы непригодны, если вероятность события мала 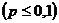. В таких случаях, когда 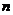велико, а 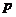мало, пользуются асимптотической формулой Пуассона.

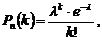
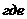
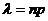(6)

Эта формула выражает закон распределения Пуассона вероятностей массовых ( 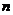велико) и редких ( 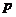мало) событий.

Одним из основных понятий массового обслуживания и надежности является понятие простейшего (Пуассоновского) потока событий.

10. Интегральная теорема Лапласа.

Теорема 4.2. Если вероятность 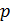наступления события 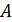в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 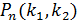того, что событие 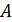появится в 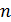испытаниях от 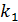до 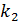раз, приближенно равна определенному интегралу

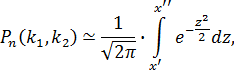
(4.1)

где

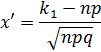и

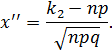
При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как неопределенный интеграл 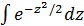не выражается через элементарные функции. Таблица для интеграла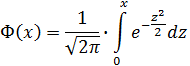

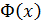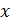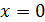приведена в конце лекционного материала (см. приложение 2). В таблице даны значения функции для положительных значений и для ; для 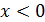пользуются той же таблицей, т.к. функция 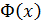нечетна, т.е.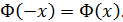

11. Функция Лапласа и ее свойства

Функция Лапласа не выражается через элементарные функции .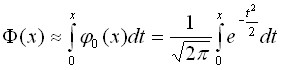

Для ее вычисления используются специальные таблицы или методы приближенного вычисления.

Функция 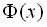обладает следующими свойствами:

;
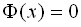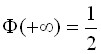; функция 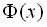– нечетная, т.е. 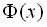= – 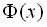, поэтому в таблицах обычно приводятся значения 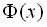только для положительных 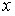; функция 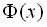– монотонно возрастающая функция (это следует из того, что 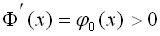). При 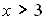, с точностью до тысячных можно принять .

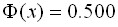Вычисление вероятности заданного отклонения. Правило «трех сигм»

Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины 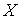по абсолютной величине меньше заданного положительного числа 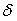, т.е. требуется найти вероятность того, что выполняется неравенство .

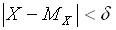На практике правило «трех сигм» применяют так: если распределение изучаемой средней величины неизвестно, но правило «трех сигм» выполняется, то есть основания полагать, что изучаемая величина распределена нормально, и наоборот.

Она приближенно равна удвоенной функции Лапласа при отклонении относительной частоты от постоянной вероятности

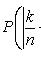
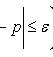
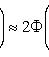
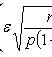
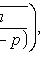
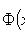
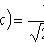
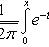
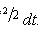
Наивероятнейшее число k₀ появления события A при n независимых испытаниях

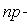
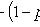
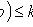
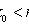
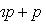(n - число испытаний; p - вероятность появления события при одном испытании).