 Общие сведения. Как отмечалось выше, функции распределения являются самым универсальным способом описания поведения результатов измерений и случайных погрешностей. Однако для их определения необходимо проведение весьма длительных и кропотливых исследований и вычислений. В большинстве случаев бывает достаточно охарактеризовать случайные величины с помощью ограниченного числа специальных параметров, основными из которых являются:
Общие сведения. Как отмечалось выше, функции распределения являются самым универсальным способом описания поведения результатов измерений и случайных погрешностей. Однако для их определения необходимо проведение весьма длительных и кропотливых исследований и вычислений. В большинстве случаев бывает достаточно охарактеризовать случайные величины с помощью ограниченного числа специальных параметров, основными из которых являются:
 - центр распределения;
- центр распределения;
 - начальные и центральные моменты и производные от них коэффициенты - математическое ожидание (МО), СКО, эксцесс, контрэксцесс и коэффициент асимметрии;
- начальные и центральные моменты и производные от них коэффициенты - математическое ожидание (МО), СКО, эксцесс, контрэксцесс и коэффициент асимметрии;
 - энтропийный коэффициент.
- энтропийный коэффициент.
 Понятие центра распределения. Координата центра распределения показывает положение случайной величины на числовой оси и может быть найдена несколькими способами. Наиболее фундаментальным является центр симметрии, т.е. нахождение такой точки Хм на оси х, слева и справа от которой вероятности появления различных значений случайной величины одинаковы и равны 0,5:
Понятие центра распределения. Координата центра распределения показывает положение случайной величины на числовой оси и может быть найдена несколькими способами. Наиболее фундаментальным является центр симметрии, т.е. нахождение такой точки Хм на оси х, слева и справа от которой вероятности появления различных значений случайной величины одинаковы и равны 0,5:
|
|
|
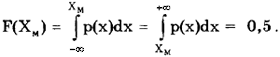
 Точку ХM называют медианой или 50% -ным квантилем. Для ее нахождения у распределения случайной величины должен существовать только нулевой начальный момент.
Точку ХM называют медианой или 50% -ным квантилем. Для ее нахождения у распределения случайной величины должен существовать только нулевой начальный момент.
 Можно определить центр распределения как центр тяжести распределения, т.е. такой точки
Можно определить центр распределения как центр тяжести распределения, т.е. такой точки  , относительно которой опрокидывающий момент геометрической фигуры, огибающей которой является кривая р(х), равен нулю:
, относительно которой опрокидывающий момент геометрической фигуры, огибающей которой является кривая р(х), равен нулю:
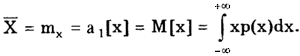
 Эта точка называется математическим ожиданием. Следует отметить, что у некоторых распределений, например распределения Коши, не существует МО, так как определяющий его интеграл расходится.
Эта точка называется математическим ожиданием. Следует отметить, что у некоторых распределений, например распределения Коши, не существует МО, так как определяющий его интеграл расходится.
При симметричной кривой р(х) в качестве центра может использоваться абсцисса моды, т.е. максимума распределения XM.
Моменты распределений. Все моменты представляют собой некоторые средние значения, причем если усредняются величины, отсчитываемые от начала координат, то моменты называют начальными, а если от центра распределения, то центральными. Начальные и центральные моменты r-го порядка определяются соответственно по формулам
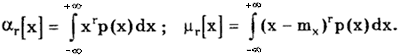
Нулевой начальный момент равен единице. Он используется для задания условия нормирования плотности распределения:
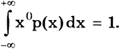
Также с помощью начального момента нулевого порядка вводится понятие медианы распределения.
Первый начальный момент - МО случайной величины:
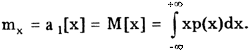
Для результатов измерений оно представляет собой оценку истинного значения измеряемой величины.
Начальные и центральные моменты случайной погрешности 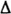 совпадают между собой и с центральными моментами результатов измерений:
совпадают между собой и с центральными моментами результатов измерений: 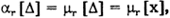 , поскольку МО случайной погрешности равно нулю. Следует также отметить, что первый центральный момент тождественно равен нулю.Важное значение имеет второй центральный момент
, поскольку МО случайной погрешности равно нулю. Следует также отметить, что первый центральный момент тождественно равен нулю.Важное значение имеет второй центральный момент
|
|
|
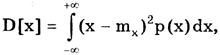
называемый дисперсией и являющийся характеристикой рассеивания случайной величины относительного МО. Значительно чаще в качестве меры рассеивания используется среднее квадратическое отклонение
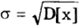
имеющее такую же размерность, как и МО. Для примера на (рис) показан вид нормального распределения при различных значениях СКО
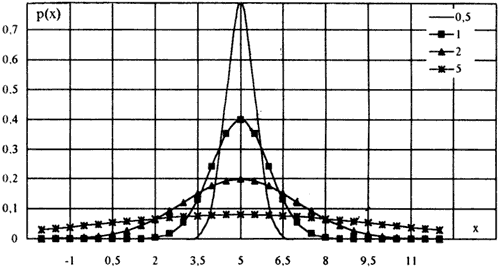
 Отдельные значения случайной погрешности предсказать невозможно. Совокупность же случайных погрешностей какого-то измерения одной и той же величины подчиняетсяопределенным закономерностям, которые являются вероятностными. Они описываются в метрологии с помощью методов теории вероятностей и математической статистики. При этом физическую величину, результат измерения которой содержит случайную погрешность, и саму случайную погрешность рассматривают как случайную величину.
Отдельные значения случайной погрешности предсказать невозможно. Совокупность же случайных погрешностей какого-то измерения одной и той же величины подчиняетсяопределенным закономерностям, которые являются вероятностными. Они описываются в метрологии с помощью методов теории вероятностей и математической статистики. При этом физическую величину, результат измерения которой содержит случайную погрешность, и саму случайную погрешность рассматривают как случайную величину.
Математическое описание непрерывных случайных величин осуществляется обычно с помощью дифференциальных законов распределения случайной величины. Эти законы определяют связь между возможными значениями случайной величины и соответствующими им плотностями вероятностей.
Наиболее распространенным при измерениях является нормальный закон распределения. Для некоторой измеряемой величины X кривая распределения плотности вероятности P(x) для закона нормального распределения имеет вид, показанный на рис. 6.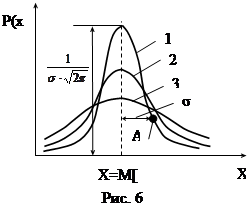
 При этом плотность вероятности (или плотность распределения) характеризует плотность, с которой распределяются значения случайной погрешности в данной точке. Плотность вероятности для закона распределения описывается уравнением:
При этом плотность вероятности (или плотность распределения) характеризует плотность, с которой распределяются значения случайной погрешности в данной точке. Плотность вероятности для закона распределения описывается уравнением:
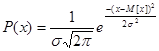
 (9)
(9)
где М[x] и σ – характеристики нормального распределения.
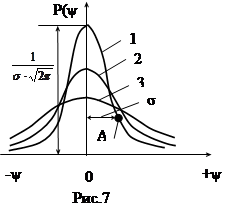
Кривую 1 можно рассматривать как кривую распределения случайной погрешности, перенеся начало координат в точку X=M[x] (рис.7).
В этом случае плотность вероятности:
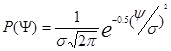 (10)
(10)
где 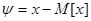 - случайная погрешность.
- случайная погрешность.
Характеристики M[x] и σ называют соответственно математическим ожиданием и среднеквадратическим отклонением. Они являются важными числовыми характеристиками случайной величины.
Математическое ожидание является тем значение величины, вокруг которого группируются результаты отдельных наблюдений, а среднеквадратическое отклонение характеризует рассеяние результатов отдельных наблюдений относительно математического ожидания. На рисунках 6 и 7 показаны кривые закона нормального распределения (кривые Гаусса) случайной величины X и ее случайной погрешности ψ при различных значениях среднеквадратического отклонения; рассеяние для кривой 3, больше, чем рассеяние для кривой 2, а рассеяние для кривой 2 – больше, чем кривой 1.
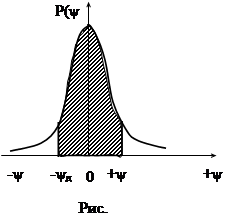 Геометрически σ определяется как расстояние от оси симметрии нормального распределения до точки А перегиба кривой распределения (Рис.6,7).
Геометрически σ определяется как расстояние от оси симметрии нормального распределения до точки А перегиба кривой распределения (Рис.6,7).
Чтобы определить вероятность P попадания результата измерения или случайной погрешности в некоторой наперед заданной интервал от -yд до +yд (рис. 8), необходимо найти площадь под кривой распределения, ограниченную вертикалями на границе интервала.
Для нормального распределения:
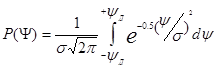 (11)
(11)
Решить интеграл (11) аналитически невозможно. Обычно он приводится в виде таблиц, позволяющих определить его значение приближенно в долях единицы.
Математическое ожидание и дисперсия являются наиболее часто применяемыми моментами, поскольку они определяют важные черты распределения: положение центра и степень разбросанности результатов относительно него. Для более подробного описания распределения используются моменты более высоких порядков.
 Третий центральный момент
Третий центральный момент
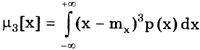
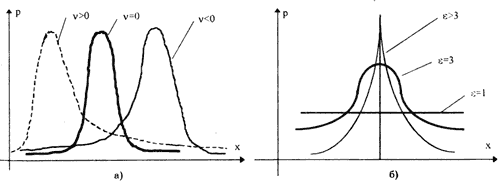
служит характеристикой асимметрии, или скошенности распределения. С его использованием вводится коэффициент асимметрии 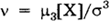 . Для нормального распределения коэффициент асимметрии равен нулю. Вид законов распределения при различных значениях коэффициента асимметрии приведен на (рис. а)
. Для нормального распределения коэффициент асимметрии равен нулю. Вид законов распределения при различных значениях коэффициента асимметрии приведен на (рис. а)
|
|
|
 Четвертый центральный момент
Четвертый центральный момент
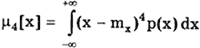
служит для характеристики плоско- или островершинности распределения. Эти свойства описываются с помощью эксцесса
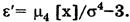
 Значения коэффициента
Значения коэффициента 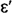 лежат в диапазоне от -2 до
лежат в диапазоне от -2 до 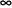 . Для нормального распределения он равен 0. Чаще эксцесс задается формулой
. Для нормального распределения он равен 0. Чаще эксцесс задается формулой
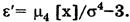
 Его значения лежат в диапазоне от 1 до
Его значения лежат в диапазоне от 1 до 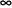 . Для нормального распределения он равен трем. Вид дифференциальной функции распределения при различных значениях эксцесса показан на (рис. б).
. Для нормального распределения он равен трем. Вид дифференциальной функции распределения при различных значениях эксцесса показан на (рис. б).

 Для удобства часто используют контрэксцесс
Для удобства часто используют контрэксцесс
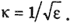
 Значения контрэксцесса лежат в пределах от 0 до 1. Для нормального закона он равен 0,577.
Значения контрэксцесса лежат в пределах от 0 до 1. Для нормального закона он равен 0,577.
 2014-01-31
2014-01-31 1244
1244








