Подходы к построению физических моделей

ФИЗИЧЕСКИЕ МОДЕЛИ ДЕФОРМИРУЕМЫХ СРЕД НА ОСНОВЕ ОПРЕДЕЛЕНИЯ ВОЛНОВЫХ П0ЛЕЙ В СЛОИСТОМ И НЕОДНОРОДНОМ ПОЛУПРОСТРАНСТВЕ

Подходы к построению физических моделей

Важные практические подходы в сейсморазведке и сейсмологии по исследованию распространения сейсмических волн могут быть отображены в рамках следующих основных методов и их модификаций: разностного, лучевого, дифракционного и матричного. Решения задач дифракционным методом получены для сред со сложной конфигурацией границ: клина, разлома, сброса и т.д. /1/; для сильно искривленных областей большой протяженности /2/, дифракции упругих волн на объектах канонической формы /3/. Однако при этом подходе получаются сложные интегральные выражения, поэтому решения здесь строятся либо для одномерных задач или исследуются частные конкретные примеры /4/. Более общие результаты получаются с помощью других упомянутых методов, они кратко рассмотрены в следующих трех подразделах. Наиболее применимым методом является матричный, подробно разобранный в работе Стародубова /5/.
1.2 Матричным методом для расчета сейсмограмм.

Матричный метод часто используется при решении прямой задачи сейсморазведки, предложенный Томсоном и Хаскеллом /6, 7/ развитый в работах МолотковаЛ.А. /8-10/, Ратниковой Л.И. /11-13/, Левшина А.Л /14/. Этот метод обеспечивает строгое математичес­кое решение ряда контактных задач динамической теории распростране­ния сейсмических волн с применением интегральных преобразований, позволяет эффективно использовать возможности современных ЭВМ для получения окончательных результатов. Матричный метод позволяет учи­тывать эффект действия источников колебаний, расположенных на сво­бодной поверхности или внутри полупространства. Этот метод быть эф­фективно использован для расчета теоретических сейсмограмм на по­верхности слоисто-однородного и неоднородного полупространств, причем неоднородности могут иметь как физический так и геометрический характер.

1.2.1 Подхода Томсона-Хаскела и его численная реализация

Рассмотрим твердое полупространство, состоящее из пачки изотропных, однородных, идеально-упругих горизонтальных слоев с прямолинейными границами раздела (Рисунок 1.1), нижний из которых име­ет бесконечную мощность. Слои характеризуются мощностью, плотностью, скоростью распространения продольных и поперечных волн ,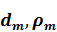

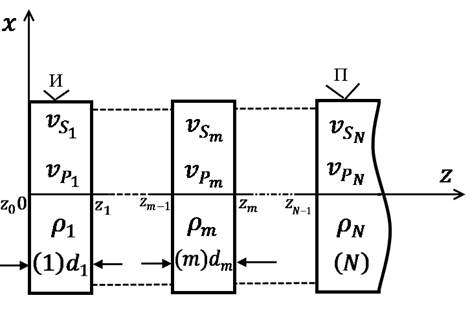
Рисунок 1.1 - Модель идеально-упругого слоисто-однородного полупространства, на свободной границе 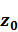которого размещены источник (И) и приемник (П).

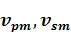Уравнение движения для перемещений 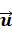, такой среды представлено в виде:

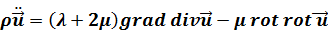
Вводятся скалярный и векторный потенциалы поля смещений 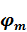, , 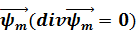с помощью которых вектор m-го слоя представлен таким образом.

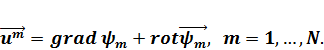(1.1)

В плоском случае вектор 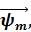преобразуется в скаляр 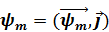где j- орт декартовой системы координат в направлении оси Y, и уравнения движения разбиваются на два независимых волновых урав­нения для упругих потенциалов 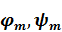описывающих распростране­ние в данной среде продольной и поперечной упругих волн:

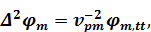(1.2)

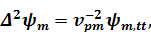(1.3)

где

Данную задачу решают в фурье-пространстве, применяя с этой целью к уравнениям (1.2), (1.3) преобразование Фурье:

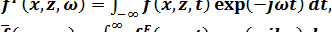(1.4)

Тогда решение системы волновых уравнений (1.2), (1.3) записы­вается в виде:

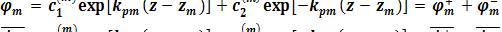(1.5)

где

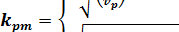, если ;

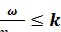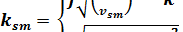, если ;

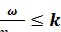Введя векторы-столбцы, элементы которых 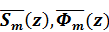зависят от параметров преобразования k, ω, получают

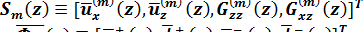(1.6)

Где 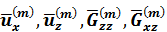- компоненты вектора смещения и напряжения в Фурье-пространстве.

Для всех точек m-го слоя имеет место соотношение

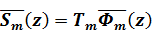(1.7)

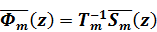(1.8)

где

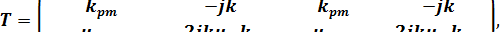(1.9)

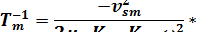
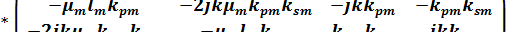(1.10)

, .

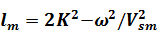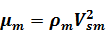Значения упругих потенциалов на (m+1)-ой границе выражаются через их значения на m -ой границе следующей рекуррентной формулой:

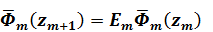(1.11)

где

(1.12) diad-обозначение диагональной матрицы.

Граничные условия в фурье-пространстве записываются следующим образом:

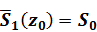, (1.13)

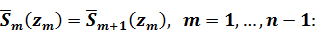(1.14)

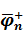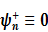= (1.15)

Равенство (1.13) задаёт условия на поверхности слоистого полупространства, причём две из компонент вектора 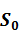(напряжения) предполагающегося заданными, а две (смещения) необходимо определить. Условие (1.14) выражает непрерывность напряжений и смещений на границах между слоями. Последнее равенство (1.15) выражает тот факт, что из нижнего полупространства волны не приходят, так как по условию задачи оно в направлении оси z не имеет границ. Со­гласно /13/ матрица-пропагатор однородного слоя определяется ре­куррентным соотношением

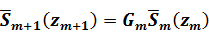. (1.16)

Из (1.7), (1.8), (1.11) следует, что

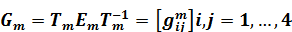(1.17)

В принятых обозначениях элементы матрицы 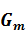имеют следующий вид /13/:

, , .

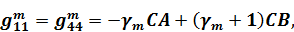
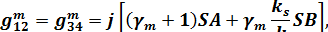
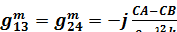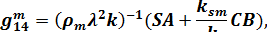
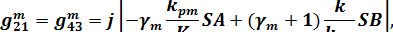
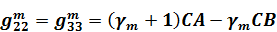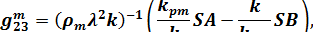
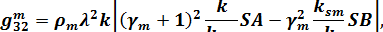
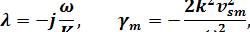
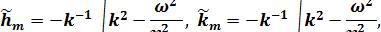
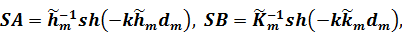
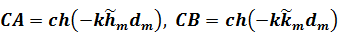(1.18)

Таким образом, на границе 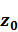слоисто-однородного полупространства из (1.7), (1.14), (1.16) имеем

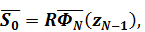(1.19)

где 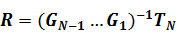– квадратная матрица 4*4.

Матрица R может быть представлена через подматрицы второго порядка

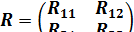. (1.20)

Если на свободной поверхности заданы фурье-трансформаторы напряжений 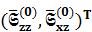, то фурье-трансформаторы смещений 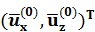, с учетом (1.15) определяются по формуле

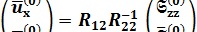. (1.21)

Для получения зависимости компонент смещения от времени на поверхности слоистого полупространства 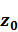производится двой­ное обратное преобразование фурье в (1.21) от ω к t и от K к x.

Рассмотренная выше классическая формулировка матричного ме­тода принадлежит Хаскеллу /7/. Численное исследование для слу­чая, когда плоская волна падает под углом на пачку идеально-упру­гих горизонтально-параллельных слоев впервые проведены Ратниковой Л.И. и Левшиным А.Л. в работе /11/. Далее эти исследования обобщены в монографиях /12, 13/.

Молотков Л.А. в работе /8/ показал, что вычислительная схема, основанная на подходе Томсона-Хаскелла /6,7/ дает ошиб­ки на высоких частотах в области предельных углов распространения волн. Для обхода этой трудности он предложил матричный метод с использованием миноров второго порядка матриц Томсона-Хаскелла, ор­ганизованных в матрицы порядка 5*5. В этой же работе Молотков Л.А. получил рекуррентные соотношения, с помощью которых матричные коэф­фициенты отражения и преломления пересчитываются с одной границы слоя на другую и выделяются заданные типы и кратности отражения-преломления из полного поля интерферирующих волн на сейсмограммах. В работах /10, 11/ исследованы выражения для коэффициентов отра­жения-преломления в области низких и высоких частот для вертикаль­но-неоднородных слоев и упруго-жидких слоистых систем.

Исследование отражения и преломления в среде с локальными неоднородностями невозможно без решения задачи о распространении волн в горизонтально-неоднородной среде. Поэтому решение такой задачи рассмотрено в следующем разделе.

1.2.2 Учет горизонтальной неоднородности среды.

Распространение поверхностных волн в среде с вертикальной и горизонтальной неоднородностью физических параметров рассматрива­лось Бабичем В.М., Молотковым И.А., Мухиной И.В; /15,16/. При этом применялся обобщенный лучевой метод. Жарков В.Н. и Оснач А.И. /16/ изучили дисперсию поверхностных волн в среде со слабой вер­тикальной и горизонтальной неоднородностью методом малого парамет­ра. В работе Кеннета Б.Л.Н. /13/ эта же теория применена для исследования распространения объемных волн в слоистой вертикально-не­однородной среде со слабой горизонтальной неоднородностью.

Рассматривается /13/ слоистая идеально-упругая среда (Рисунок 1.2) между параллельными слоями которой выполнены условия жесткого контакта. Плоскость совпадает с границей верх­него слоя 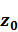, которая является свободной. Нижний слой 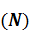однородный и бесконечный в направлении оси 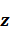, характеризуется скоростями продольной и поперечной волн 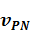, , 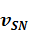полностью 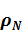. Каждый промежуточный слой (1, … N-1) 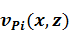, 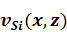и полностью 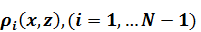неоднород­ной среды.

Считается, что напряжение и смещение не зависят от y коор­динаты и изменения физических характеристик 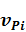, , 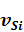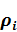в латеральном направлении (по координате х) являются небольши­ми, так что поле смещений, рассеянное на такой неоднородности, по порядку меньше поля, рассеянного на неоднородности физических ха­рактеристик в вертикальном направлении (по координате 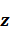). Ста­вится задача определения зависимости от времени поля смещений на границе 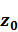полупространства, когда источник колебаний 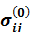на­ходится на 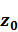и это поле удовлетворяет условию равенства нулю на бесконечности.

Определение поля смещений 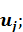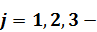расчет теоретический сейсмограммы для указанной модели - состоит в решении системы уравнении движения 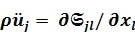, когда выполняется закон Гука:

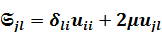, (1.22)

Где 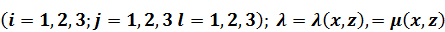коэффициенты Ламе, 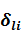– символ Кронекера,

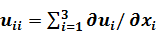
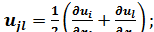
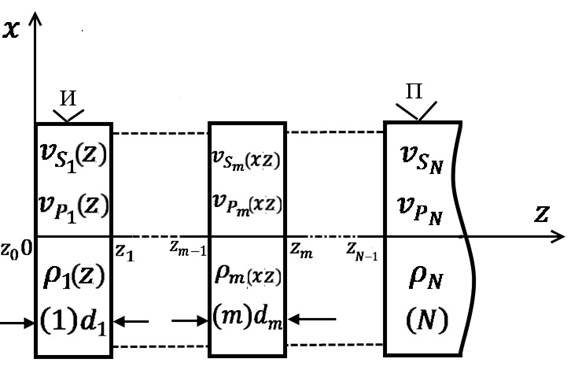
Рисунок 1.2 - Модель идеально-упругого горизонтально-слоистого полупространства, в m- ом слое которого плотность и скорость распределения продольных и поперечных волн являются неоднородными по двум координатам 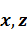. Источник (И) и приемник (П) размещены на свободной границе полупространства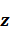

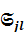-компоненты напряжений в декартовых координатах, значение индексов 1,2,3 эквиваленты обозначению .

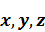Подразумевается, что после напряжений-смещений неявно зависит от времени 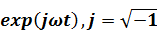. 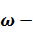угловая частота, тогда равенства (1.22) можно записать в матричном виде /13/. Для волн P-SV:

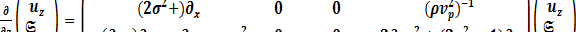, (1.23)

где , ;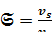

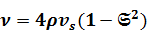для волн SH:

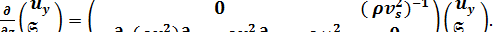(1.24)

Если представить неоднородность в виде

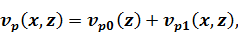
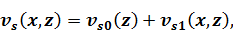
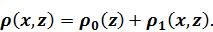
и ввести обозначения

,

;

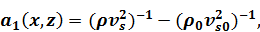
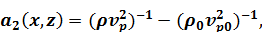
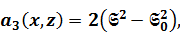
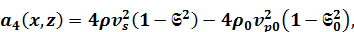
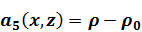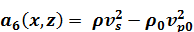тогда уравнения (1.23), (1.24) можно записать в общем виде

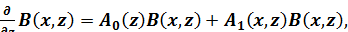(1.25)

где 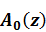– операторная матрица, относящаяся к латерально-однородной среде, 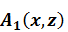– операторная матрица, зависящая от «мер неоднородности» .

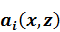Для P-SV – волн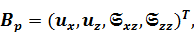

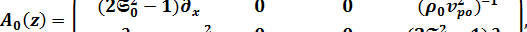
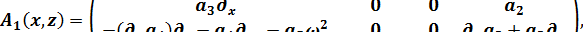
где ,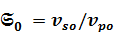

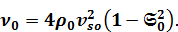
Для случая SH волн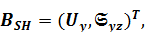

,

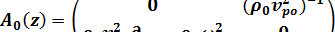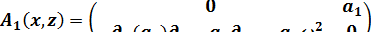
В результате применения к (1.25) преобразование Фурье (1.4) по (1.4) и 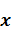учета во втором члене леммы Бореля, за­ключающейся в том, что Фурье-преобразование произведения матриц равно свертке их фурье-трансформант, получают

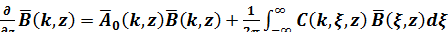, (1.26)

где для P-SV волн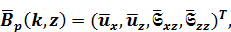

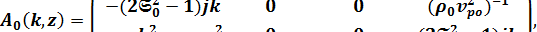
Для SH волн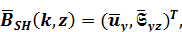

,

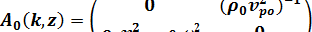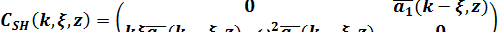
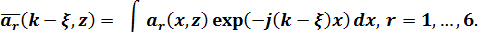
Если правый член в уравнении (1.26) нулевая матрица, то оно описывает латерально-однородную среду.

Из теории обыкновенных дифференциальных уравнений известно, что есл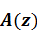и и 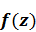матрицы комплексных функций, то при исходных условиях 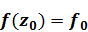решение уравнения.

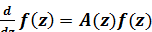(1.27)

имеет вид

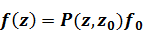(1.28)

где 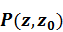– матрица- пропагатор для вертикально-неоднородного слоя /77/

Если 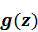матрица порядка n*1, то при тех же исходных условиях решение уравнения

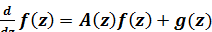(1.29)

можно представить в виде

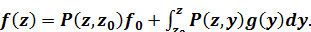(1.30)

Уравнение (1.26) для 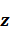совпадает с (1.29), когда

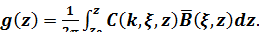(1.31)

Тогда решение уравнение (1.36) имеет вид

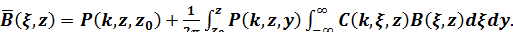(1.32)

Когда 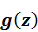, определяемое формулой (1.31), нулевая матрица, уравнение (1.26) приобретает вид, аналогичный (1.27) и его решением является

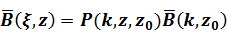(1.33)

По условию задачи

,

,

.

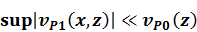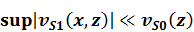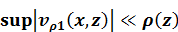В работе /16/ для представления поля 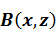делятся следующее допущение:

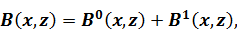(1.34)

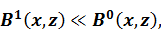(1.35)

где 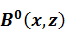– поле напряжения-смещения в латерально- однородной среде, 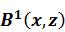– поле, рассеянное на горизонтальных неоднородностях.

В результате, применения к (1.34) преобразования (1.4) после подстановки в (1.32) получают окончательно

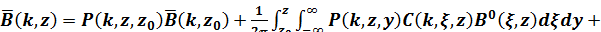
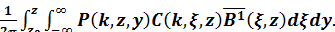(1.36)

Крайний правый член в управлении (1.36) определяет мультипольное рассеяние в 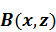. При условии (1.35)

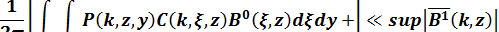
мультипольное рассеяние не учитывается.

Далее показано, что такое неравенство можно привести к виду

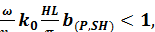(1.37)

где 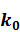- максимальное значение используемого 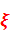, 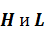– вертикальный и горизонтальный размер неоднородности,

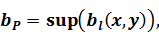
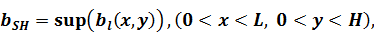
где , , , , , ;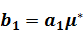

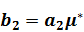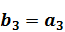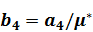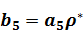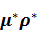- усредненный коэффициент Ламе и плотность по толщине, содержащей неоднородность.

Если крайний правый член в (1.36) отбросить, как величи­ну второго порядка малости, то решение уравнения (1.26) для рассеянного поля можно представить в виде

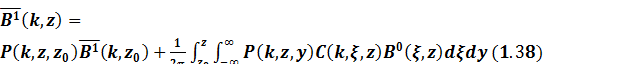
Таким образом вклад неоднородности представляется как неко­торый источник, распределенный в объеме, размеры и физические характеристики которого определяются неравенством (1.37). Когда условие (1.37) не удовлетворяется, тогда имеют место мультипольные эффекты и в рассеянном поле 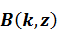надо учитывать члены второго и более высоких порядков малости.

Далее при рассмотрении распространения волн в горизонтально- неоднородной среде Кеннетом применен матричный метод для слоистой; среды, при этом каждый пропагатор 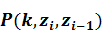уже описывал распространение волн в i-ом слое. В работе автора /16/ предложена методика расчета сейсмограмм на свободной границе полупростран­ства, когда горизонтальная неоднородность находится в одном из слоев. Эта методика изложена во втором разделе.

Широкий класс задач сейсмологии допускает при теоретическом рассмотрении сейсмических волн применять закон Гука для идеально- упругого тела. Однако, актуальной является необходимость учета тех особенностей распространения и затухания упругих колебаний, которые нельзя объяснить в рамках теории для идеально-упругой модели среды.

Известен ряд подходов к учету диссипации энергии упругих волн в моделях сред. Способы учета диссипации энергии распростра­няющихся волн и расчета, получающейся при этом дисперсии фазовой скорости и добротности для моделей реальных сред, рассмотрены в следующем подразделе.

1.3 Распространение сейсмических волн при влиянии неидеальной упругости среды.

Отдельное место в матричном методе занимают задачи для сред, в которых происходит потеря энергии при распространении волн. Матричный метод разработан для диссипативной модели с последействием /12/, для вязкоупругих сред и для пористых сред с применением теории Френкеля-Био. В работе /12/ изложена методика расчета теоретических сейсмограмм на поверхности слоистой неидеально-упругой среды (Рисунок 1.1), когда каждый слой характеризуется дополнительно добротностями 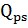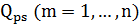распространения продольных и поперечных волн. Источник колебаний находится на бесконечности в положительном направлении оси Z.